현이의 개발 이야기

도넛과 막대 그래프 - Lv 2 문제 풀이

프로그래머스 > Java로 코테풀기2024. 08. 23. 15:36

https://school.programmers.co.kr/learn/courses/30/lessons/258711?language=java

구현 중심의 문제로, 제시된 조건만 파악하면 쉽게 풀리는 문제였다.

문제에서 파악해야 하는 핵심 조건이 무엇이었는지를 알아보고, 이를 해결하기 위한 구현 과정을 살펴보자.

문제 풀이

문제에서는 도넛 묘양, 막대 모양, 8자 모양의 세 종류의 그래프를 제시합니다. 그리고 이 세 그래프에 속하지 않은 하나의 노드가 추가되어 모든 그래프를 연결합니다.

그래프 별 노드의 특징

먼저, 각 그래프에 속한 노드와 새로 추가한 노드의 특징을 살펴봅시다.

도넛 모양 그래프의 노드

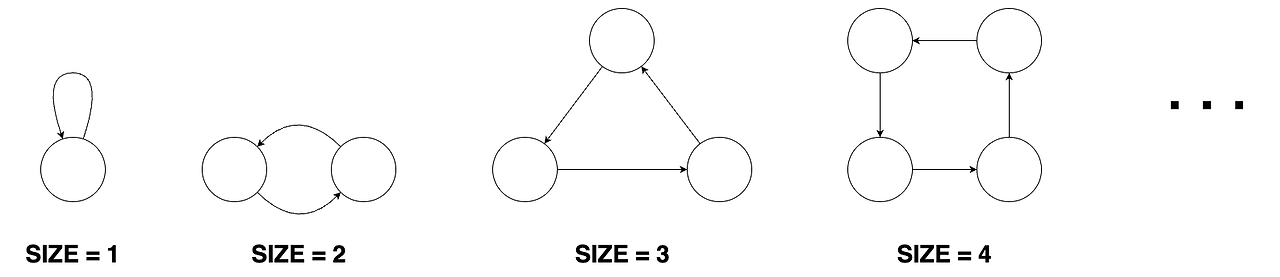
도넛 모양 그래프의 모든 노드는 다음의 특징을 갖습니다.

하나의 나가는 간선과 하나의 들어오는 간선이 있습니다.
간선을 따라가다보면 자기 자신을 만나게 됩니다.

막대 모양 그래프의 노드

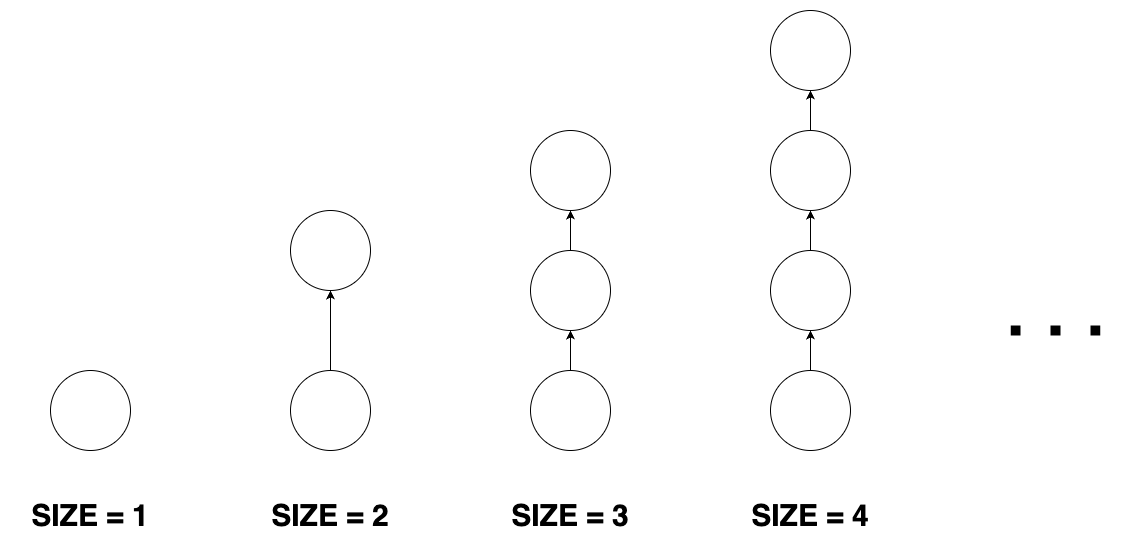
막대 그래프의 모든 노드는 다음의 특징을 갖습니다.

최대 하나의 나가는 간선과, 최대 하나의 들어오는 간선이 있습니다.
간선을 따라가다보면 막다른 노드에 도달합니다.

8자 모양 그래프의 노드

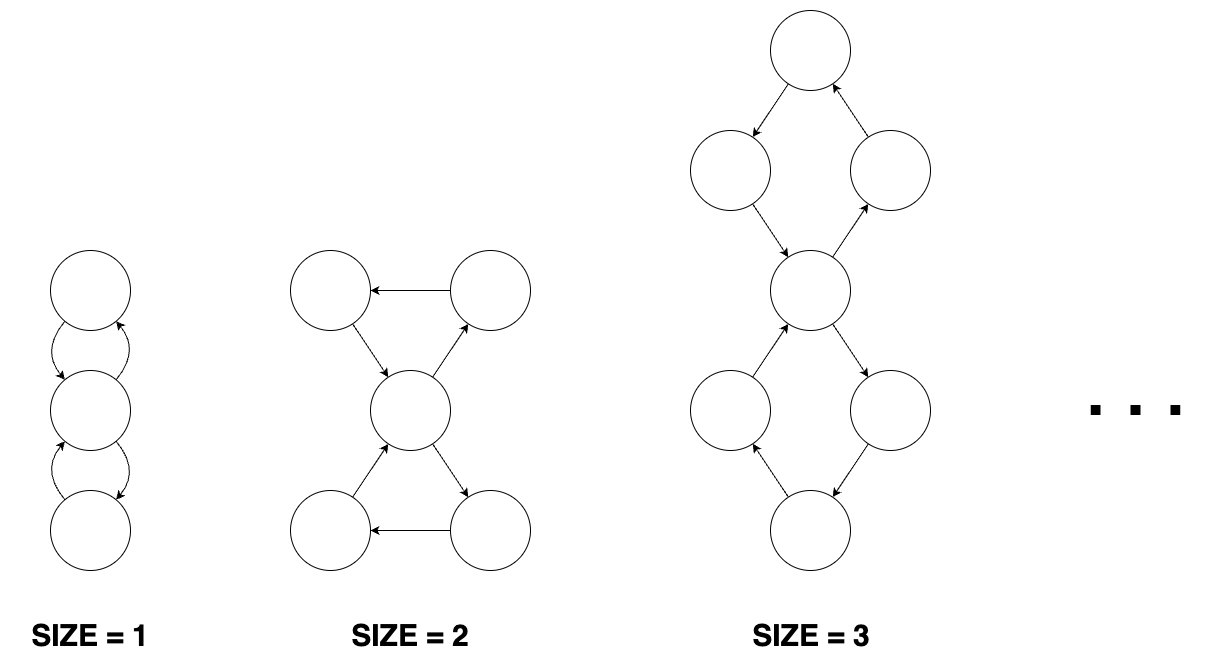
8자 모양 그래프의 모든 노드는 다음의 특징을 갖습니다.

하나의 들어오는 간선과 나가는 간선 또는 두 개의 들어오는 간선과 나가는 간선이 있습니다.
간선을 따라가다보면 두 개의 들어오는 간선과 나가는 간선을 갖는 노드를 만나게 됩니다.

새로 삽입된 노드

새로 삽입된 노드는 두 개 이상의 그래프를 연결하기 때문에 다음의 특징을 갖습니다.

들어오는 간선이 없습니다.
두 개 이상의 나가는 간선이 있습니다.

삽입된 노드 찾아 그래프 분리하기

위에서 살펴 본 노드의 특징을 활용하여 삽입된 노드를 찾아, 그래프들을 종류별로 분리할 수 있습니다.

삽입된 노드 찾기

새로 삽입된 노드의 특징 중 하나인 들어오는 간선이 없는 노드를 생각해 봅시다.

막대 모양 그래프의 시작 노드가 이러한 특징을 가질 수 있습니다. 그러나 나가는 간선이 두 개 이상이어야 한다는 점을 생각하면 이를 만족하는 노드는 새로 삽입된 노드 뿐입니다.

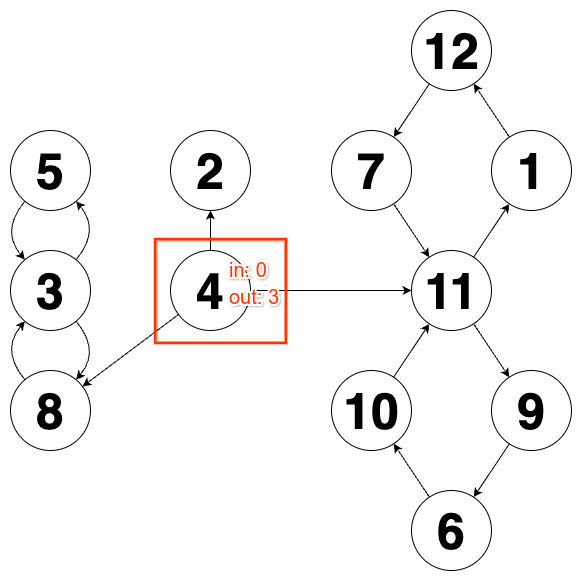
따라서 모든 노드를 순회하며, 들어오는 간선이 없고, 나가는 간선이 두 개 이상인 노드를 찾는다면, 해당 노드가 삽입된 노드임을 알 수 있습니다.

그래프 분리하기

삽입된 노드를 찾은 후에, 해당 노드와 연결된 간선들을 모두 끊으면 종류별로 명확히 분리된 그래프를 얻을 수 있습니다.

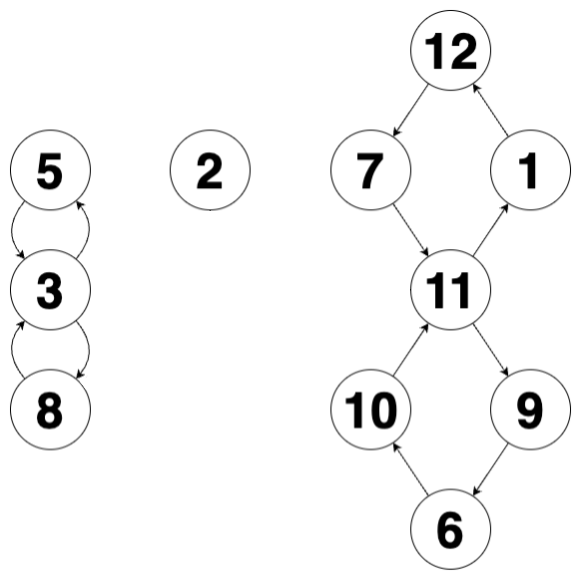
위 그림에서 알 수 있듯이, 삽입된 노드를 제거하면 왼쪽부터 8자 모양 그래프, 막대 모양 그래프, 8자 모양 그래프임을 쉽게 알 수 있습니다.

그래프 구분하기

그래프를 분리했으니 이제 각 그래프가 어떤 모양인지를 검사해야 합니다.

이 과정은 앞서 살펴본 노드의 특징을 활용하면 쉽게 할 수 있습니다.

임의의 한 노드로부터 출발하여 간선을 따라가다가,

막다른 노드에 도달한다면: 막대 모양 그래프
나가는 간선과 들어오는 간선의 수가 모두 2인 노드에 도달한다면: 8자 모양 그래프
출발 노드로 돌아온다면: 도넛 모양 그래프

여기서 주의할 점은, 8자 모양 그래프에 대한 검사를 도넛 모양 그래프 검사보다 우선 해야 한다는 것입니다.

8자 모양 그래프도 한 노드로부터 간선을 따라가다보면 자기 자신이 나오게 됩니다. 하지만 그 이전에 8자 모양 그래프의 중심 노드를 거쳐야 하기 때문에 이를 우선 검사하여 8자 모양 그래프와 도넛 모양 그래프를 구분합니다.

코드

이를 코드로 구현하면 다음과 같습니다.

import java.util.*;
import java.util.function.Function;

class Solution {
    enum NodeType {
        DONUT,
        LINEAR,
        EIGHT,
    }
    
    static class Node {
        List<Node> outs = new ArrayList<>();
        List<Node> ins = new ArrayList<>();
        NodeType type;
    }
    
    private static Map<Integer, Node> constructNodes(int[][] edges) {
        Map<Integer, Node> nodes = new HashMap<>();
        
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];
            
            if (!nodes.containsKey(u)) nodes.put(u, new Node());
            if (!nodes.containsKey(v)) nodes.put(v, new Node());
            
            Node from = nodes.get(u);
            Node to = nodes.get(v);
            
            from.outs.add(to);
            to.ins.add(from);
        }
        
        return nodes;
    }
    
    private static int findInsertedNodeKey(Map<Integer, Node> nodes) {
        for (int key : nodes.keySet()) {
            Node node = nodes.get(key);
            if (node.ins.size() == 0 && node.outs.size() >= 2) {
                return key;
            }
        }
        
        // Unreachable
        return -1;
    }
    
    private static int removeInsertedNode(Map<Integer, Node> nodes) {
        int insertedKey = findInsertedNodeKey(nodes);
        Node inserted = nodes.remove(insertedKey);
        
        for (Node node : inserted.ins) {
            node.outs.remove(inserted);
        }
        for (Node node : inserted.outs) {
            node.ins.remove(inserted);
        }
        return insertedKey;
    }
    
    private static Node getUnvisitedNext(Node node, List<Node> direction) {
        for (Node next : direction) {
            if (next.type == null) return next;
        }
        return null;
    }
    
    private static void mark(Node node, NodeType type, Function<Node, List<Node>> getDirection) {
        do {
            node.type = type;
            node = getUnvisitedNext(node, getDirection.apply(node));
        } while (node != null);
    }
    
    private static NodeType check(Node node) {
        Node initial = node;
        while (true) {
            if (node.outs.size() == 0) {
                mark(node, NodeType.LINEAR, n -> n.ins);
                return NodeType.LINEAR;
            } else if (node.ins.size() == 2 && node.outs.size() == 2) {
                mark(getUnvisitedNext(node, node.outs), NodeType.EIGHT, n -> n.outs);
                return NodeType.EIGHT;
            } 
            
            node = getUnvisitedNext(node, node.outs);
            if (node == null) {
                // Unreachable
                break;
            }
            
            if (node == initial) {
                mark(node, NodeType.DONUT, n -> n.outs);
                return NodeType.DONUT;
            }   
        };
        return null;
    }
    
    public int[] solution(int[][] edges) {
        Map<Integer, Node> nodes = constructNodes(edges);
        int insertedKey = removeInsertedNode(nodes);
        
        int donut = 0;
        int linear = 0;
        int eight = 0;
        
        for (Node node : nodes.values()) {
            if (node.type != null) continue;
            
            switch (check(node)) {
                case LINEAR:
                    linear += 1;
                    break;
                case EIGHT:
                    eight += 1;
                    break;
                case DONUT:
                    donut += 1;
                    break;
            }
        }
        
        return new int[] { insertedKey, donut, linear, eight };
    }
}

로그인이 필요합니다.

로그인