현이의 개발 이야기

행렬과 연산 - Lv 4 문제 풀이

프로그래머스 > Java로 코테풀기2024. 06. 20. 11:00

https://school.programmers.co.kr/learn/courses/30/lessons/118670

정확성과 효율성 테스트가 같이 있는 문제이다.

코딩 테스트에서 이런 문제를 만나게 되면 효율성 테스트의 조건을 먼저 보아야 한다.
효율성 테스트를 해결할 수 있는 풀이는 정확성 테스트도 해결할 수 있지만,
정확성 테스트를 해결할 수 있는 풀이는 효율성 테스트를 통과하지 못할 수 있기 때문이다.

만약 처음부터 정확성 테스트의 조건을 해결하는 풀이를 고민한다면,
한 문제를 두 번 풀어야 하는 상황이 발생할 수 도 있다.

따라서 효율성 테스트를 먼저 고민하고, 정 모르겠다 싶으면 정확성 테스트의 조건을 보도록 하자.

이번 포스트에서는 효율성 테스트에 대한 풀이만 다루겠다.

문제 풀이

제한 사항으로 시간 복잡도 유추하기

문제의 제한 사항을 살펴봄으로써 문제가 원하는 해답의 시간 복잡도를 유추해 봅시다.

제한 사항에 따르면 행렬의 크기는 최대 100,000입니다. 이를 N이라고 합시다.
또, 연산의 개수도 최대 100,000입니다. 이를 M이라고 합시다.

만약 하나의 연산에 대해 행렬 전체를 업데이트 해야 한다면 연산 한 번에 O(N)의 시간 복잡도가 소요되어, 전체 시간 복잡도는 O(MN)이 됩니다.
이는 최대 100억에 해당하는 수치로, 시간 복잡도 제한인 1억을 훌쩍 넘겨버립니다.

operations를 순회하며 연산을 하나씩 적용하는 것은 줄일 수 없는 시간 복잡도입니다.
O(M)은 이미 정해져있고, 여기에 곱해지는 시간 복잡도인 연산 하나당 소요되는 시간 복잡도를 줄여야 한다는 의미입니다.
M 자체로 이미 10만이기 때문에 연산 하나 당 소요되는 시간 복잡도를 O(1), 혹은 적어도 O(logN)으로 줄여야 합니다.

연산에 대한 시간 복잡도 생각하기

O(logN)은 특별한 시간 복잡도입니다.
O(logN)이라는 시간 복잡도를 만들어 내는 접근법들은 대부분 그 유형이 정해져 있습니다.
트리, 이분 탐색, 분할 정복 등이 있는데, 이들 모두 배열을 회전시키는 연산과는 딱히 연결성이 없어 보입니다.

따라서 연산에 상수 시간인 O(1)이 소요되는 것이 가장 그럴듯합니다.

시간 복잡도 기반으로 연산 접근하기

연산에 상수 시간이 소요된다면 아주 간단한 연산으로 해결된다는 의미입니다.
ShiftRow의 경우 숫자가 섞이는 것이 아니기 때문에 행렬에서 가장 윗 행이 어디인지를 추적하는 것으로 상수 시간 안에 해결이 됩니다.

문제는 Rotate입니다. 숫자들의 순서가 바뀌게 되므로 실제 숫자들이 어떻게 움직이는지를 추적해야 합니다.
이를 어떻게 상수 시간 안에 해결할 수 있을까요?

Rotate 연산

문제에서 주어진 회전 연산을 생각해 보면, 행렬의 겉에서만 숫자들이 회전합니다.

즉, 가장자리를 상하좌우 4개로 나누어 생각해보면, 한쪽 가장자리에서 빠진 숫자는 다른 가장자리로 들어가게 됩니다.
이는 LinkedList로 해결할 수 있습니다.
행렬의 상하좌우를 관리하는 LinkedList를 만들어, 회전 연산 때 원소 하나를 제거하고 다른 리스트로 넣어주는 방식입니다.

LinkedList는 가장 앞 원소와 가장 뒤에 있는 원소의 추가/삭제 연산에 대한 시간 복잡도가 O(1)이므로 상수 시간 안에 해결할 수 있습니다.
rotate 연산을 실제로 상수 시간 안에 해결할 수 있게 된 것입니다.

그런데 이 LinkedList를 구성하는 방법에는 다음과 같이 여러 가지가 있습니다.

LinkedList를 구성하는 방법들

이 중 어떤 방식으로 리스트를 구성해야 할까요?

Rotate 연산만 생각하면 어떤 방식을 채택하든 큰 상관이 없습니다.
그렇다면 ShiftRow 연산까지 생각해 봅시다.

ShiftRow 연산

앞에서 배열의 행 인덱스를 이용해 상수 시간 안에 연산을 해결했는데,
Rotate 연산을 해결하려다 보니 배열의 실제 구성이 바뀌게 되었습니다.

ShiftRow 연산은 모든 숫자들을 한 칸씩 아래로 내립니다.
이를 쉽게 구현하기 위해서는 LinkedList가 열 방향으로, 즉 세로로 구성되어 있어야 합니다.

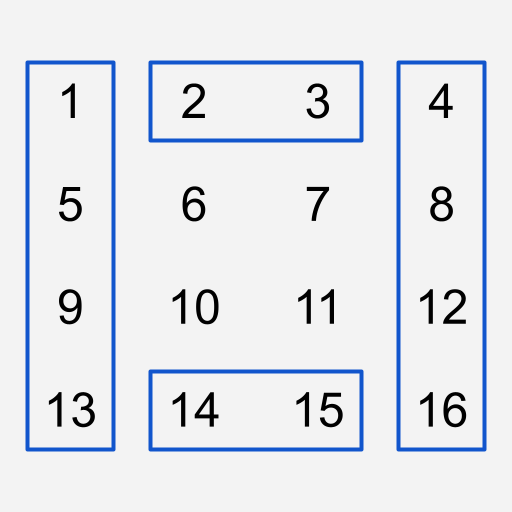
이렇게 구현해 놓게 되면 ShiftRow 연산이 발생했을 시에 가장 왼쪽과 오른쪽 LinkedList는 마지막 숫자를 빼서, 자신의 가장 앞에 넣어주면 됩니다.

가운데 남은 숫자들의 경우 ShiftRow 연산이 발생하면 가장자리로 갈 수 있게 됩니다.
따라서 Rotate 연산에 포함될 경우를 대비해 미리 다음과 같이 LinkedList에 넣어줍니다.

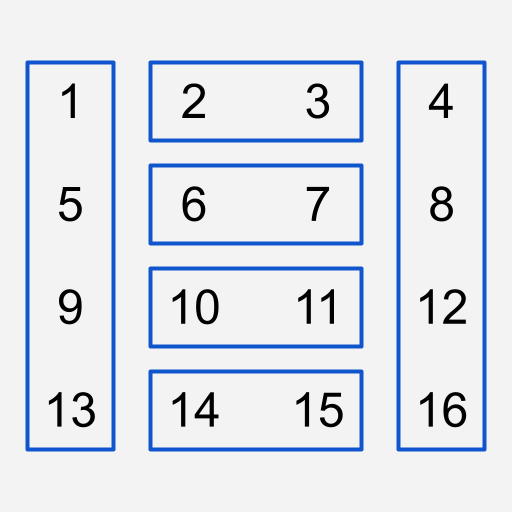Rotate 연산을 대비한 LinkedList들

이제 ShiftRow 연산은 가운데에 있는 LinkedList 자체를 한 칸씩 내려주면 됩니다.

이를 위해 가운데 LinkedList 전체를 또 다른 LinkedList로 감싸줍니다.

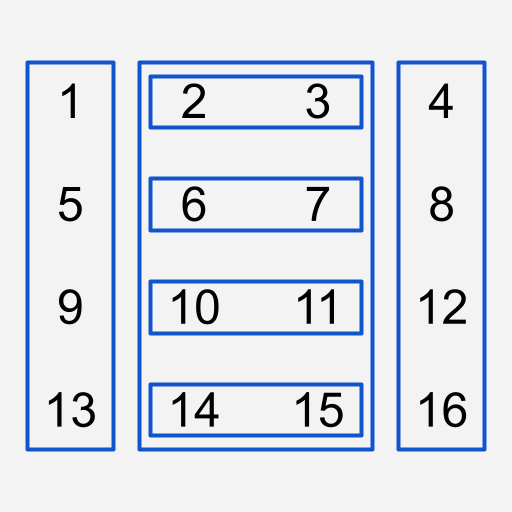최종 LinkedList 구성

ShiftRow와 Rotate 연산을 모두 상수 시간 안에 처리할 수 있기 때문에, 연산을 처리하는 시간 복잡도는 O(M)이 됩니다.

전체 시간 복잡도는 행렬의 원소를 한 번씩 읽고 쓰는 O(N)과 연산을 처리하는 O(M) 중 더 큰 시간 복잡도가 됩니다.

이는 O(N + M) 으로 표기할 수 있습니다.

LinkedList 구성 살펴보기

위에서 구성한 LinkedList를 이용하면 Rotate와 ShiftRow 연산을 상수 시간 안에 할 수 있습니다.

Rotate 연산에는 다음의 LinkedList들이 관여합니다.

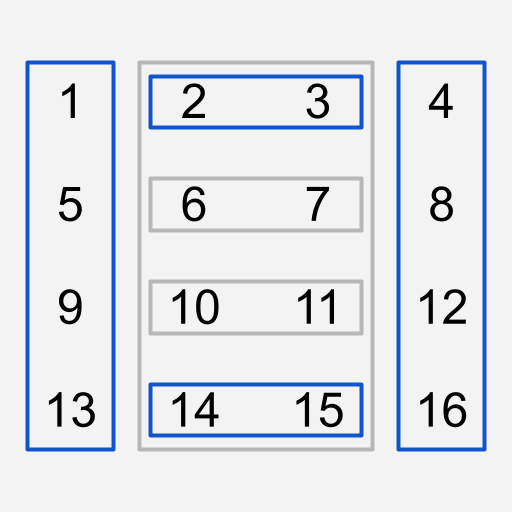Rotate 연산에 관여하는 LinkedList 들

ShiftRow 연산에는 다음의 LinkedList들이 관여합니다.

ShiftRow 연산에 관여하는 LinkedList들

구현하기

Matrix 클래스 만들기

행렬에 관련된 연산을 처리하기 위한 클래스 Matrix를 다음과 같이 작성해 줍니다.

private static class Matrix {
  public final int w;
  public final int h;
  
  Matrix(int[][] rc) {
    w = rc[0].length;
    h = rc.length;
  }
}

LinkedList 구성하기

Matrix 클래스는 이차원 배열 rc를 생성자에 입력받아, 위에서 살펴본 LinkedList로 구성해주어야 합니다.

이를 위해 왼쪽 left, 오른쪽 right, 그리고 가운데의 LinkedList를 가리키는 body를 다음과 같이 선언해 줍니다.

private final LinkedList<Integer> left = new LinkedList<>();
private final LinkedList<Integer> right = new LinkedList<>();
private final LinkedList<LinkedList<Integer>> body = new LinkedList<>();

이 세 LinkedList들은 생성자에서 다음과 같이 채워줄 수 있습니다.

for (int i = 0; i < h; i++) {
  LinkedList<Integer> bodyRow = new LinkedList<>();
  for (int j = 0; j < w; j++) {
    if (j == 0) {
      left.add(rc[i][j]);
    } else if (j == w - 1) {
      right.add(rc[i][j]);
    } else {
      bodyRow.add(rc[i][j]);
    }
  }
  body.add(bodyRow);
}

ShiftRow 연산

ShiftRow는 세 LinkedList의 가장 마지막 원소를 제거하고, 가장 앞 원소에 추가해 주는 연산을 해주는 연산입니다.

void shiftRow() {
  left.addFirst(left.removeLast());
  right.addFirst(right.removeLast());
  body.addFirst(body.removeLast());
}

LinkedList의 addFirst(), removeLast() 연산은 상수 시간이므로, shiftRow() 메서드 또한 상수 시간이 걸림을 다시 한번 확인할 수 있습니다.

Rotate 연산

Rotate는 가장자리에 있는 LinkedList들끼리 원소를 하나씩 밀어주는 연산입니다.

void rotate() {
  LinkedList<Integer> firstBodyRow = body.getFirst();
  LinkedList<Integer> lastBodyRow = body.getLast();
  
  firstBodyRow.addFirst(left.removeFirst());
  lastBodyRow.addLast(right.removeLast());
  
  right.addFirst(firstBodyRow.removeLast());
  left.addLast(lastBodyRow.removeFirst());
}

마찬가지로 모든 메서드가 상수 시간을 가져, rotate() 연산 또한 상수 시간임을 확인할 수 있습니다.

여기에서 주의해야 할 점이, left, right에서 bodyRow들로 원소를 보내는 작업의 순서가 더 빨라야 한다는 점입니다.

bodyRow에서 left, right으로 원소를 보내는 작업을 먼저 해주게 된다면, 행렬의 가로길이가 2인 경우 bodyRow는 빈 LinkedList가 되는데, 이때 NoSuchElementException이 발생하게 됩니다.

이차원 배열 변환

마지막으로, 연산이 종료된 행렬을 다시 이차원 배열로 변환시켜주어야 합니다.
이는 build() 메서드에 다음과 같이 작성합니다.

int[][] build() {
  int[][] matrix = new int[h][w];

  Iterator<Integer> leftIterator = left.iterator();
  Iterator<Integer> rightIterator = right.iterator();
  Iterator<LinkedList<Integer>> bodyIterator = body.iterator();
  for (int i = 0; i < h; i++) {
    matrix[i][0] = leftIterator.next();
    matrix[i][w - 1] = rightIterator.next();
    
    Iterator<Integer> bodyRowIterator = bodyIterator.next().iterator();
    for (int j = 1; j < w - 1; j++) {
      matrix[i][j] = bodyRowIterator.next();
    }
  }
  
  return matrix;
}

이 부분을 작성할 때, get()을 사용하여 LinkedList의 원소에 접근하지 않도록 주의해야 합니다.
LinkedList는 ArrayList와 달리, get()에 O(N)의 시간 복잡도가 소요되기 때문입니다.

어차피 LinkedList의 원소들을 순차적으로 접근하므로 Iterator를 이용하여 원소 참조에 불필요한 시간을 소요하지 않도록 합니다.

solution() 메서드

solution 메서드에서는 주어진 rc를 이용해 Matrix를 생성하고,
주어진 연산을 모두 적용해 준 다음,
이차원 배열로 변환하여 반환합니다.

public int[][] solution(int[][] rc, String[] operations) {
  Matrix matrix = new Matrix(rc);
  
  for (String operation : operations) {
    switch (operation) {
      case "ShiftRow":
        matrix.shiftRow();
        break;
      case "Rotate":
        matrix.rotate();
        break;
    }
  }
  
  return matrix.build();
}

전체 코드

import java.util.Iterator;
import java.util.LinkedList;

public class Solution {
  private static class Matrix {
    public final int w;
    public final int h;
    private final LinkedList<Integer> left = new LinkedList<>();
    private final LinkedList<Integer> right = new LinkedList<>();
    private final LinkedList<LinkedList<Integer>> body = new LinkedList<>();

    Matrix(int[][] rc) {
      w = rc[0].length;
      h = rc.length;

      for (int i = 0; i < h; i++) {
        LinkedList<Integer> bodyRow = new LinkedList<>();
        for (int j = 0; j < w; j++) {
          if (j == 0) {
            left.add(rc[i][j]);
          } else if (j == w - 1) {
            right.add(rc[i][j]);
          } else {
            bodyRow.add(rc[i][j]);
          }
        }
        body.add(bodyRow);
      }
    }

    void shiftRow() {
      left.addFirst(left.removeLast());
      right.addFirst(right.removeLast());
      body.addFirst(body.removeLast());
    }

    void rotate() {
      LinkedList<Integer> firstBodyRow = body.getFirst();
      LinkedList<Integer> lastBodyRow = body.getLast();

      firstBodyRow.addFirst(left.removeFirst());
      lastBodyRow.addLast(right.removeLast());

      right.addFirst(firstBodyRow.removeLast());
      left.addLast(lastBodyRow.removeFirst());
    }

    int[][] build() {
      int[][] matrix = new int[h][w];

      Iterator<Integer> leftIterator = left.iterator();
      Iterator<Integer> rightIterator = right.iterator();
      Iterator<LinkedList<Integer>> bodyIterator = body.iterator();
      for (int i = 0; i < h; i++) {
        matrix[i][0] = leftIterator.next();
        matrix[i][w - 1] = rightIterator.next();

        Iterator<Integer> bodyRowIterator = bodyIterator.next().iterator();
        for (int j = 1; j < w - 1; j++) {
          matrix[i][j] = bodyRowIterator.next();
        }
      }

      return matrix;
    }
  }

  public int[][] solution(int[][] rc, String[] operations) {
    Matrix matrix = new Matrix(rc);

    for (String operation : operations) {
      switch (operation) {
        case "ShiftRow":
          matrix.shiftRow();
          break;
        case "Rotate":
          matrix.rotate();
          break;
      }
    }

    return matrix.build();
  }
}

로그인이 필요합니다.

로그인