현이의 개발 이야기

쌍둥이 빌딩 숲 - Lv 4 문제 풀이

프로그래머스 > Java로 코테풀기2024. 06. 19. 11:00

https://school.programmers.co.kr/learn/courses/30/lessons/140105

처음 그림을 봤을 때 생긴 건 스택으로 푸는 히스토그램 문제랑 비슷하게 생겼다고 생각했다.
제목에 쌍둥이가 들어가서 짝을 찾아야 하나 하는 생각이 들어서 그런 것도 있는 것 같다.

하지만 문제를 읽어보니 전혀 스택과는 관련 없어보였다. 오히려 처음에 히스토그램 문제를 접했을 때 떠올리는 점화식을 활용한 재귀적 접근으로 풀리는 문제였다.

문제 풀이

같은 높이를 가지는 빌딩 사이에는 그보다 높은 빌딩이 존재하지 않습니다.

이 조건에 집중해 봅시다.

이것에 따르면 빌딩들이 배치된 상태에서 가장 작은 빌딩을 배치하려고 할 때,

가장 작은 빌딩의 쌍은 항상 붙어 있어야 한다는 것을 알 수 있습니다.

예를 들어, 다음과 같이 빌딩이 배치되어 있습니다.

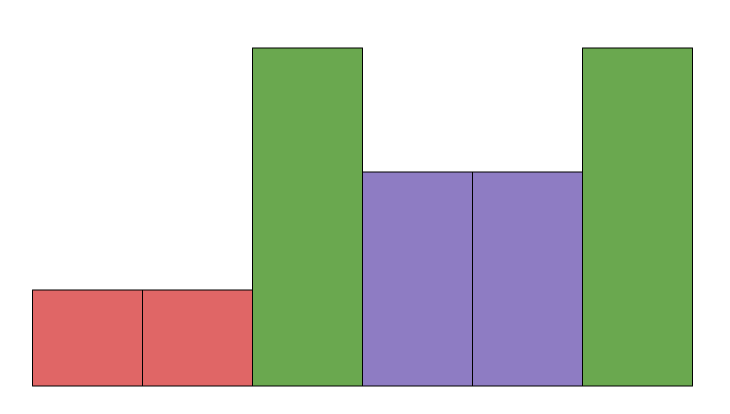3개 건물 쌍의 배치 상태

가장 작은 노란색 빌딩 쌍을 추가한다고 생각해봅시다.

다음의 경우는 불가능합니다.

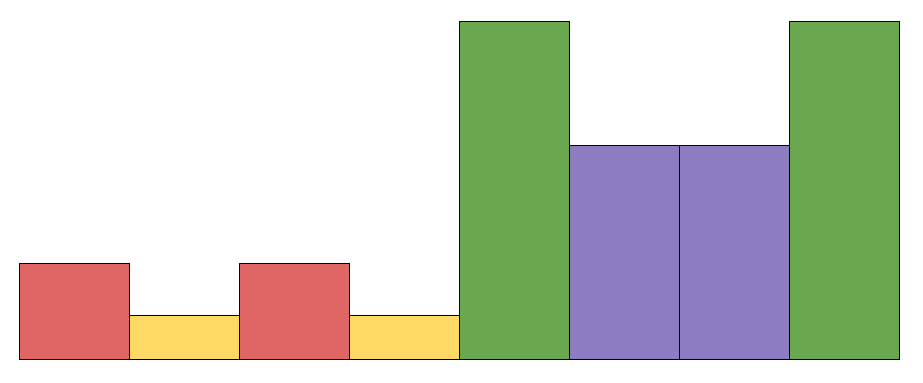불가능한 경우

반면, 다음과 같이 노란색 빌딩 쌍을 붙인다면, 이미 있는 건물 사이에 어떤 곳에 배치하던 가능한 경우가 됩니다.

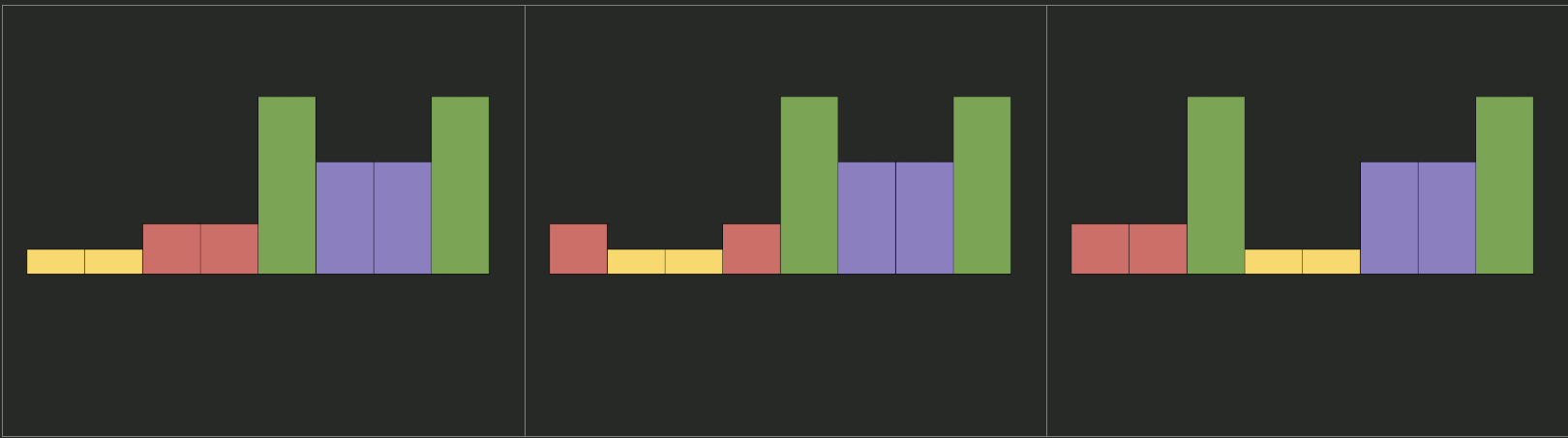가능한 경우들

위의 그림에서 알 수 있는 중요한 점은 노란색 건물을 가장 앞에 배치하는 경우가 아니면, 노란색 건물은 보이지 않는다는 것입니다.

이를 활용하면 문제를 풀기 위한 점화식을 세울 수 있습니다.

다음과 같이 상태를 정의해봅시다.

(n, c): n개의 건물 쌍을 배치했을 때, c개의 건물이 보이는 경우의 수

  - (0, 0) = 1
  - (0, c) = 0
  - (n, 0) = 0
  - c > n인 경우 (n, c) = 0

n개의 건물 쌍을 배치 하기 위해서는:

n-1개의 건물 쌍을 배치
가장 작은 건물 쌍을 어디에 배치할 것인지 정하기

가장 작은 건물 쌍의 위치와 이 건물 쌍을 제외한 건물들의 배치가 다르기 때문에 중복이 발생하지 않습니다.
또, 가장 작은 건물은 어떤 경우이던 항상 존재하므로 누락이 발생하지도 않습니다.

가장 작은 건물을 맨 앞에 배치하는 경우:

1개의 경우의 수가 있습니다.
보이는 건물의 수가 1개 늘어납니다.

가장 작은 건물을 다른 건물 사이에 배치하는 경우:

2(n-1)개의 경우의 수가 있습니다.
보이는 건물의 수는 늘어나지 않습니다.

이를 이용하면, n개의 건물을 배치했을 때 c개의 건물이 보이기 위해서는, 이전 단계인 n-1개의 건물을 배치했을 때:

c-1개의 건물이 보이는 경우
1. 하나의 건물이 더 보여야 하므로 가장 작은 건물을 맨 앞에 배치
2. 1개의 경우의 수
c개의 건물이 보이는 경우
1. 보이는 건물의 수가 늘어나지 않아야 하므로 다른 건물 사이에 배치
2. 2(n-1)개의 경우의 수

즉, 다음과 같이 점화식을 쓸 수 있습니다.

(n, c) = (n-1, c-1) + (n-1, c) * 2(n-1)

시간 복잡도

하나의 상태를 계산할 때 별도의 반복이 필요하지 않습니다.
따라서 상태의 개수에 해당하는 시간 복잡도가 소요게 되어 O(nc)의 시간 복잡도를 갖습니다.

문제의 조건에 따라 n과 c의 최댓값은 100이므로 매우 넉넉한 시간 복잡도입니다.
최댓값 조건이 1000이어도 충분한 시간 복잡도가 됩니다.

전체 코드

import java.util.Arrays;

public class Solution {
  private static final int DIV = 1_000_000_007;

  private static final int[][] mem = new int[101][101];

  static {
    for (int[] row : mem) {
      Arrays.fill(row, -1);
    }

    for (int n = 0; n <= 100; n++) {
      mem[n][0] = 0;
      for (int c = n + 1; c <= 100; c++) {
        mem[n][c] = 0;
      }
    }
    mem[0][0] = 1;
  }

  public int solution(int n, int count) {
    if (mem[n][count] != -1) return mem[n][count];

    long sum = solution(n - 1, count - 1);
    sum += (long) solution(n - 1, count) * 2 * (n - 1);

    return mem[n][count] = (int) (sum % DIV);
  }
}

원래 static 블럭을 잘 사용하지 않는데, 이번 문제에서는 solution() 메서드 자체를 재귀시킬 수 있어서 사용했습니다.

로그인이 필요합니다.

로그인