현이의 개발 이야기

경사로의 개수 - Lv. 4 문제 풀이

프로그래머스 > Java로 코테풀기2024. 06. 17. 10:36

https://school.programmers.co.kr/learn/courses/30/lessons/214290

2023년 현대 모비스 알고리즘 경진대회 예선 문제라고 한다.
현대 모비스에서 소프트웨어를 강조하기 위해 주최하는 경진대회라고 하는데 어마어마한 상품으로 상당히 화제였었다.
1위 상이 무려 아이오닉 5... 차 한대가 상품이었다.
2등상은 1,000만원 3등상은 500만원으로 역대급 대회였다.

하지만 그런 만큼 진짜 쟁쟁하신 분들이 나오셨다고...
2024년 현대 모비스 알고리즘 경진대회도 총 상금 1억 7천만원이 걸려 있고, 프로그래머스에서 6월 25일까지 접수받고 있다.

=> 2024년 현대 모비스 알고리즘 경진대회 접수

어쨌든 이 문제는 프로그래머스에서 Lv4로 등재되었고, 2차원 배열과 이동 가능한 조건이 주어졌을 때, 이동 가능한 경로의 개수를 찾는 문제이다.

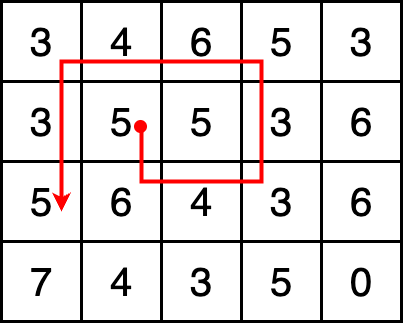
문제 풀기

제한 사항으로 접근법 떠올려보기

문제에서 주어진 제한 사항은 다음과 같습니다.

3 ≤ grid의 길이 = n ≤ 8
3 ≤ grid[i]의 길이 = m ≤ 8
0 ≤ grid[i][j] ≤ 1,000
1 ≤ d의 길이 ≤ 100
1 ≤ k ≤ 10^9 그리드의 크기는 작은 반면, k의 크기는 10억으로 매우 크다는 것을 알 수 있습니다.

k는 d를 반복해야 하는 횟수이므로 k번에 해당하는 만큼 반복을 해야 할 것 같기는 한데, 그 값을 보니 k번 반복을 해서는 안됩니다.

그렇다면 log의 시간 복잡도를 가지는 분할 정복을 떠올릴 수 있습니다.

k를 반으로 나눠가며 연산하는 분할 정복이라면 O(logK)번 만에 k번에 해당하는 반복을 계산해낼 수 있을 것입니다.

이제 문제를 분할 정복에 맞도록 정의할 수 있는지를 확인하면 됩니다.

부분 문제 정의하기

주어진 문제를 분할 정복을 활용해 k번 반복되는 부분 문제로 만들어야 합니다.

문제에서 k번 반복되는 것은 d를 적용하는 횟수입니다.

따라서 d를 적용하는 횟수의 가장 최소 횟수인 1인 문제를 먼저 풀고, 이를 k번 반복하는 것으로 접근할 수 있습니다.

(x1, y1, x2, y2): (x1, y1)에서 (x2, y2)로 d를 이용하여 이동하는 경로의 수

(x1, y1, x2, y2)는 제 책 [취업과 이직을 위한 프로그래머스 코딩 테스트 문제 풀이 전략: 자바편]에서 소개한 문제를 나타내기 위한 표기법으로, 문제를 정의하기 위해 필요한 변수의 집합이라고 생각하시면 됩니다.

더 작은 부분 문제

그런데 위의 문제를 풀기 위해서는 경로를 파악해야 합니다.

이는 다시 부분 문제를 정의하여 다음과 같이 재귀적으로 해결할 수 있습니다.

(x1, y1, x2, y2, di): (x1, y1)에서 (x2, y2)로 d[di]~d[끝]을 이용해서 갈 수 있는 경우의 수 \
        = (x1, y1, x, y, i) * (x, y, x2, y2, d.length - i) => 모든 x, y와 di <= i <= d.length에 대한 반복 합

(x1, y1, x2, y2, di)를 풀면, (x1, y1, x2, y2) = (x1, y1, x2, y2, 0)으로 구할 수 있게 됩니다.

이 부분에 해당하는 코드

private static final int DIV = 1_000_000_007;
private static final int[] dx = {1, 0, -1, 0};
private static final int[] dy = {0, 1, 0, -1};

private static int count(
    int x1, int y1, int x2, int y2, int di, int[][] grid, int[] d, int[][][][][] mem) {
  // Memoization
  if (mem[di][x1][y1][x2][y2] != -1) {
    return mem[di][x1][y1][x2][y2];
  }
  
  // 종료 조건
  if (di == d.length) {
    if (x1 == x2 && y1 == y2) {
      return mem[di][x1][y1][x2][y2] = 1;
    } else {
      return mem[di][x1][y1][x2][y2] = 0;
    }
  }
  
  // 재귀
  int sum = 0;
  for (int i = 0; i < 4; i++) {
    int nx = x1 + dx[i];
    int ny = y1 + dy[i];
    try {
      if (grid[ny][nx] == grid[y1][x1] + d[di]) {
        sum += count(nx, ny, x2, y2, di + 1, grid, d, mem);
        sum %= DIV;
      }
    } catch (IndexOutOfBoundsException ignored) {
    }
  }
  return sum;
}

private static int[][][][] buildCountMatrix(int[][] grid, int[] d) {
  int w = grid[0].length;
  int h = grid.length;
  
  // [i][x1][y1][x2][y2]: (x1, y1) -> (x2, y2)를 d[i] ~ d[끝]을 이용해 갈 수 있는 경우의 수
  int[][][][][] mem = new int[d.length + 1][w][h][w][h];
  
  for (int di = d.length; di >= 0; di--) {
    for (int x1 = 0; x1 < w; x1++) {
      for (int y1 = 0; y1 < h; y1++) {
        for (int x2 = 0; x2 < w; x2++) {
          Arrays.fill(mem[di][x1][y1][x2], -1);
          for (int y2 = 0; y2 < h; y2++) {
            mem[di][x1][y1][x2][y2] = count(x1, y1, x2, y2, di, grid, d, mem);
          }
        }
      }
    }
  }
  return mem[0];
}

부분 문제 시간 복잡도

(x1, y1, x2, y2, di)의 경우 재귀가 진행됨에 따라 반복되는 부분 문제이기 때문에 한 단계의 상태를 구하기 위한 시간 복잡도와 상태의 개수를 이용해 시간 복잡도를 계산할 수 있습니다.

하나의 상태를 구하기 위해서는 d의 길이만큼 반복하고, x, y에 대해서도 반복합니다.

1 <= d의 길이 <= 100
3 <= x, y, <= m = 8 주어진 조건이 위와 같으므로시간 복잡도는 **O(dm²)**이 되고, 최댓값을 대입했을 때 6,400이므로 이 부분 문제는 충분한 시간 복잡도를 가지고 있음을 알 수 있습니다.

분할 정복

(x1, y1, x2, y2)를 해결할 수 있으니, 이를 이용해 k번 반복하는 문제를 해결해야 합니다.

이 문제는 다음과 같이 정의할 수 있습니다.

(x1, y1, x2, y2, r): (x1, y1)에서 (x2, y2)로 d를 r번 이용하여 이동하는 경우의 수
        = (x1, y1, x, y, r / 2) * (x, y, x2, y2, r / 2) => r이 짝수일 경우
        = (x1, y1, x, y, r / 2) * (x, y, x2, y2, r / 2) * (x1, y1, x2, y2, 1) => r이 홀수일 경우
(x1, y1, x2, y2, 1) = (x1, y1, x2, y2)

모든 x1, y1, x2, y2에 대해 이를 반복한다면 답을 구할 수 있습니다.

그런데 문제가 있습니다. 이 부분 문제는 메모이제이션을 적용할 수 없다는 것입니다.

r의 크기는 최대 10억으로, 이는 메모이즈하기에는 너무 큰 값입니다.

모든 출발점과 도착점에 대해서 같은 연산을 해야 한다는 점을 생각하면 비슷하지만 조금 다른 접근 방식을 생각할 수 있습니다.

행렬 연산

한 점에서 다른 점으로 이동하는 경로의 수는 행렬로 표현할 수 있습니다.

사실, 이미 행렬로 표현되어 있습니다.

문제 (x1, y1, x2, y2)가 풀어낸 답이 바로 그 행렬입니다.

이 문제의 결과는 [x1, y1, x2, y2]의 4차원 배열이 됩니다.

이 배열의 각 원소는 (x1, y1)에서 (x2, y2)로 이동할 수 있는 경로의 수를 가지고 있습니다.

지금 우리가 구해야 하는 것은 (x1, y1)에서 출발하고, (x2, y2)에 도착하지만, 그 과정 중에 어떠한 좌표 (x, y)를 경유하면서 이동하는 경우의 수입니다.

이는 행렬의 곱셈과 같습니다. 즉, 행렬을 k번 거듭제곱하는 것으로 모든 좌표에 대해 같은 연산을 적용할 수 있게 됩니다.

이 부분에 해당하는 코드

private int[][][][] multiply(int[][][][] a, int[][][][] b) {
  int w = a.length;
  int h = a[0].length;
  
  int[][][][] m = new int[w][h][w][h];
  for (int x1 = 0; x1 < w; x1++) {
    for (int y1 = 0; y1 < h; y1++) {
      for (int x2 = 0; x2 < w; x2++) {
        for (int y2 = 0; y2 < h; y2++) {
          for (int x = 0; x < w; x++) {
            for (int y = 0; y < h; y++) {
              m[x1][y1][x2][y2] += (int) (((long) a[x1][y1][x][y] * b[x][y][x2][y2]) % DIV);
              m[x1][y1][x2][y2] %= DIV;
            }
          }
        }
      }
    }
  }
  return m;
}

private int[][][][] power(int[][][][] matrix, int power) {
  if (power == 1) {
    return matrix;
  }
  if (power == 2) {
    return multiply(matrix, matrix);
  }
  
  int[][][][] result = power(power(matrix, power / 2), 2);
  if (power % 2 == 1) {
    result = multiply(result, matrix);
  }
  return result;
}

행렬 연산 시간 복잡도

한 번의 재귀 단계에 x1, y1, x2, y2, x, y에 대해서 반복합니다.

반복의 깊이는 log k이므로 전체 시간 복잡도는 **O(log k * m^6)**이 됩니다.

마무리

이제 결과 행렬에서 모든 원소를 순회하며 경로의 개수 합을 구해주면 됩니다.

이 부분에 해당하는 코드

public int solution(int[][] grid, int[] d, int k) {
  int[][][][] matrix = buildCountMatrix(grid, d);
  matrix = power(matrix, k);
  
  int count = 0;
  
  int w = matrix.length;
  int h = matrix[0].length;
  
  //noinspection ForLoopReplaceableByForEach Suppress for better readability.
  for (int x1 = 0; x1 < w; x1++) {
    for (int y1 = 0; y1 < h; y1++) {
      for (int x2 = 0; x2 < w; x2++) {
        for (int y2 = 0; y2 < h; y2++) {
          count += matrix[x1][y1][x2][y2] % DIV;
          count %= DIV;
        }
      }
    }
  }
  
  return count;
}

전체 시간 복잡도

전체 풀이는 다음의 단계를 따라갑니다.

(x1, y1, x2, y2, di)를 해결하는 부분
1. 시간 복잡도: O(dm²)
행렬의 거듭제곱을 계산하는 부분
1. 시간 복잡도: O(log k * m^6)
경로 합을 구하는 부분
1. 시간 복잡도: O(m⁴) 따라서 전체 시간 복잡도는 O(dm²) + O(log k * m^6) + O(m⁴) = O((d + log k * m⁴)m²)이 되고,

최댓값을 고려했을 때 d < log k * m⁴d이므로 **O(log k * m^6)**이 됩니다.

제한 사항을 고려해 최댓값을 대입하면 약 784만이라는 값이 나와, 충분한 시간 복잡도라는 것을 알 수 있습니다.

전체 코드

import java.util.Arrays;

public class Solution {
  private static final int DIV = 1_000_000_007;
  private static final int[] dx = {1, 0, -1, 0};
  private static final int[] dy = {0, 1, 0, -1};

  private static int count(
      int x1, int y1, int x2, int y2, int di, int[][] grid, int[] d, int[][][][][] mem) {
    // Memoization
    if (mem[di][x1][y1][x2][y2] != -1) {
      return mem[di][x1][y1][x2][y2];
    }

    // 종료 조건
    if (di == d.length) {
      if (x1 == x2 && y1 == y2) {
        return mem[di][x1][y1][x2][y2] = 1;
      } else {
        return mem[di][x1][y1][x2][y2] = 0;
      }
    }

    // 재귀
    int sum = 0;
    for (int i = 0; i < 4; i++) {
      int nx = x1 + dx[i];
      int ny = y1 + dy[i];

      try {
        if (grid[ny][nx] == grid[y1][x1] + d[di]) {
          sum += count(nx, ny, x2, y2, di + 1, grid, d, mem);
          sum %= DIV;
        }
      } catch (IndexOutOfBoundsException ignored) {
      }
    }
    return sum;
  }

  private static int[][][][] buildCountMatrix(int[][] grid, int[] d) {
    int w = grid[0].length;
    int h = grid.length;

    // [i][x1][y1][x2][y2]: (x1, y1) -> (x2, y2)를 d[i] ~ d[끝]을 이용해 갈 수 있는 경우의 수
    int[][][][][] mem = new int[d.length + 1][w][h][w][h];

    for (int di = d.length; di >= 0; di--) {
      for (int x1 = 0; x1 < w; x1++) {
        for (int y1 = 0; y1 < h; y1++) {
          for (int x2 = 0; x2 < w; x2++) {
            Arrays.fill(mem[di][x1][y1][x2], -1);
            for (int y2 = 0; y2 < h; y2++) {
              mem[di][x1][y1][x2][y2] = count(x1, y1, x2, y2, di, grid, d, mem);
            }
          }
        }
      }
    }

    return mem[0];
  }

  private int[][][][] multiply(int[][][][] a, int[][][][] b) {
    int w = a.length;
    int h = a[0].length;

    int[][][][] m = new int[w][h][w][h];
    for (int x1 = 0; x1 < w; x1++) {
      for (int y1 = 0; y1 < h; y1++) {
        for (int x2 = 0; x2 < w; x2++) {
          for (int y2 = 0; y2 < h; y2++) {
            for (int x = 0; x < w; x++) {
              for (int y = 0; y < h; y++) {
                m[x1][y1][x2][y2] += (int) (((long) a[x1][y1][x][y] * b[x][y][x2][y2]) % DIV);
                m[x1][y1][x2][y2] %= DIV;
              }
            }
          }
        }
      }
    }
    return m;
  }

  private int[][][][] power(int[][][][] matrix, int power) {
    if (power == 1) {
      return matrix;
    }
    if (power == 2) {
      return multiply(matrix, matrix);
    }

    int[][][][] result = power(power(matrix, power / 2), 2);
    if (power % 2 == 1) {
      result = multiply(result, matrix);
    }

    return result;
  }

  public int solution(int[][] grid, int[] d, int k) {
    int[][][][] matrix = buildCountMatrix(grid, d);
    matrix = power(matrix, k);

    int count = 0;

    int w = matrix.length;
    int h = matrix[0].length;

    //noinspection ForLoopReplaceableByForEach Suppress for better readability.
    for (int x1 = 0; x1 < w; x1++) {
      for (int y1 = 0; y1 < h; y1++) {
        for (int x2 = 0; x2 < w; x2++) {
          for (int y2 = 0; y2 < h; y2++) {
            count += matrix[x1][y1][x2][y2] % DIV;
            count %= DIV;
          }
        }
      }
    }

    return count;
  }
}

로그인이 필요합니다.

로그인