아날로그 시계 - Lv 2 문제 풀이 (실수 비교 안하기)
프로그래머스> Java로 코테풀기2024. 06. 09. 05:07
주어진 시간 범위 내에서 초침이 분침 / 시침과 겹치는 횟수를 세는 문제이다.
문제 이해하기
다음과 같은 조건들로 인해 제약 사항이 생긴다.
- 각 바늘은 연속적으로 움직인다.
- 바늘이 겹치는 시간이나 각도가 실수이기 때문에 정확한 비교는 힘들다.
- 1초 안에 초침이 다른 하나의 바늘과 두 번 겹치는 경우는 없다.
- 초침-분침, 초침-분침 과 같이 분침과 두 번 겹칠 일은 없다.
- 다만, 초침-분침, 초침-시침과 같이 서로 다른 두 바늘과 겹칠 수는 있다.
간단히 생각하면, 그냥 1초씩 시간을 흘려가면서 각 바늘의 각도를 계산해가면서 초침이 분침이나 시침의 각도를 넘어서는 횟수를 세주면 될 것이다. 딱 여기까지라면 정말 Lv2인 이 문제에 알맞는 난이도라고 생각했을 것이다.
하지만 문제는 시침과 분침, 초침이 한 번에 겹치게 되면 한 번으로 세주어야 하는 데에서 발생했다. 위 접근법은 1초 내에 초침이 분침 또는 시침과 겹친 적이 있는지를 판별할 수는 있지만, 셋 모두가 동시에 겹쳤다는 것을 판단할 수는 없다. 분침-시침이 겹치는 것을 별도로 판별했다고 하더라도, 이 시점이 초침과 겹쳐지는 시점과 달라질 수 있기 때문에 정확하지 않다.

세 바늘이 동시에 겹쳤는지를 판단하기 위해서는 1초 내에서도 언제 겹쳤는지 정확한 시간을 계산하여 비교하던가, 바늘이 겹쳤을 때의 정확한 각도를 계산하여 비교할 수 있어야 한다.
나이브한 접근 - 실수 비교
이게 Lv 2라고? 하는 생각이 들어 다른 사람들의 풀이를 찾아보았다. 놀랍게도 대다수의 사람들이 무려 실수 비교를 통해 바늘이 겹치는 것을 검사하고 있었다. 세 바늘의 각도를 double로 표현하고, 이 각도가 서로 일치하는지를 검사한 것이다.
조금 세게 말하자면, 정말 말도 안되는 풀이라고 생각했다.
프로그래밍을 처음 공부할 때 배우는 것이 실수형의 한계이다. 컴퓨터는 0과 1로 한정된 비트 수를 사용하여 실수를 표현하기 때문에 실수를 정확하게 표현할 수 없고, 오차가 발생한다는 것은 누구나 알고 있다.
따라서 실수형을 다룰 때에는 정확한 값을 가지고 있을 것이라는 생각 자체를 하면 안된다. 다시 말해, 실수형에 == 연산은 해당 값에 부동 소수점 오차가 없다는 완벽한 근거 없이는 절대 해서는 안되는 연산이라는 것이다. 이로 인해 실수형은 대부분 비교 연산을 수행하거나, 일정 수준의 threshold를 두고, 해당 오차 범위 안의 값인지를 검사한다.
그런데 정확성이 중요한 코딩 테스트에서 실수형 비교를 통해 문제를 해결한다니, 말이 안된다고 생각했다.
이러한 방법을 사용한 풀이가 통과된 것은, 단순히 시침, 분침, 초침이 겹치는 시간이 12시 00분 00초 밖에 없기 때문이다. 이 때는 각도가 0이므로 소수점 오차가 발생하지 않는다. 만약 다른 각도에서 세 바늘이 겹치는 현상이 발생했다면, 이 코드들은 통과하지 못했을 것이다.
또, 정확히 12시에만 세 바늘이 겹친다는 것을 알고 있었다면 실수형 비교를 할 이유가 없다. 그저 시간이 12시 정각인지를 검사하는 것을 통해 훨씬 간단하게 체크할 수 있기 때문이다. 다시 말해, 각도를 실수로 표현하고, 이를 동등 비교하는 것은 이 문제 풀이에서 나와서는 안되는, 운으로 통과하는 케이스라고 생각한다.
구현으로 풀기
세 바늘의 각도를 비교해야 한다는 것에는 이견이 없다. 다만, 이를 실수형으로 나타내고 푸는 것이 위험하다는 것이다. 다행히도, 빡센 구현을 통해 부동 소수점 오차 걱정 없이 문제를 해결할 수 있다.
Fraction 클래스
이를 해결하기 위해서는 각도를 분수로 나타내면 된다. 앞선 포스트 자바로 분수 나타내기에서 다룬 Fraction 클래스를 이용하면 각도를 온전히 나타낼 수 있다. 몇몇 메서드가 이 문제에 맞춰 수정되었지만, 큰 뼈대는 같으니 설명 없이 코드만 첨부한다.
private static class Fraction implements Comparable<Fraction> {
public final long numerator;
public final long denominator;
public Fraction(int value) {
this(value, 1);
}
public Fraction(long numerator, long denominator) {
long gcd = gcd(Math.abs(numerator), Math.abs(denominator));
this.numerator = numerator / gcd;
this.denominator = denominator / gcd;
}
public Fraction add(int value) {
return new Fraction(numerator + value * denominator, denominator);
}
public Fraction add(Fraction other) {
long numerator = this.numerator * other.denominator + this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction subtract(Fraction other) {
long numerator = this.numerator * other.denominator - this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction multiply(Fraction other) {
long numerator = this.numerator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction divide(Fraction other) {
return multiply(other.inverse());
}
public Fraction inverse() {
if (numerator == 0) {
throw new ArithmeticException("Cannot inverse zero.");
}
return new Fraction(denominator, numerator);
}
public Fraction mod(int value) {
return new Fraction(numerator % (value * denominator), denominator);
}
public double value() {
return (double) numerator / denominator;
}
@Override
public boolean equals(Object object) {
if (this == object) return true;
if (object == null || getClass() != object.getClass()) return false;
Fraction other = (Fraction) object;
return numerator == other.numerator && denominator == other.denominator;
}
@Override
public int compareTo(Fraction f) {
if (equals(f)) {
return 0;
} else if (value() < f.value()) {
return -1;
} else {
return 1;
}
}
private static long gcd(long a, long b) {
if (b == 0) return a;
return gcd(b, a % b);
}
}
Clock 클래스
시계를 나타내는 Clock 클래스이다. 세 바늘의 각도와 현재 시간, 초침이 다른 바늘과 겹치는 연산을 수행해줄 클래스가 될 것이다.
먼저, 각 바늘이 초 당 몇 도나 회전하는지를 Fraction으로 나타내어준다.
시침은 360도를 12(시간)* 60(분) * 60(초) 만에 돈다.
분침은 360도를 60(분) * 60(초) 만에 돈다.
초침은 360도를 60(초) 만에 돈다.
시침은 360도를 12(시간)* 60(분) * 60(초) 만에 돈다.
분침은 360도를 60(분) * 60(초) 만에 돈다.
초침은 360도를 60(초) 만에 돈다.
private static class Clock {
private static final Fraction HOUR_APS = new Fraction(360, 12 * 60 * 60);
private static final Fraction MINUTE_APS = new Fraction(360, 60 * 60);
private static final Fraction SECOND_APS = new Fraction(360, 60);
}
다음으로, 현재 시간과 각 바늘의 각도를 Fraction으로 나타내어준다.
private Fraction time;
private Fraction hourAngle;
private Fraction minuteAngle;
private Fraction secondAngle;
생성자에서는 현재 시간을 입력 받고, 이에 맞게 각 바늘의 각도를 계산해준다.
여기서 중요하게 생각해야 할 점이 바로 초침이 시침이나 분침보다 빠르다는 점이다.
이는 초침이 각도 상 뒤에 있어야 (즉, 더 작은 각도를 가지고 있어야) 분침과 시침을 따라잡는 연산이 쉬워진다는 의미이다.
따라서, 분침이나 시침이 초침보다 더 작은 각도를 가지고 있다면, 한 바퀴를 추가로 회전시켜 (360을 더하여) 더 큰 각도를 가지고 있게 만들어준다.
public Clock(int time) {
this.time = new Fraction(time);
alignAngles();
}
private void alignAngles() {
hourAngle = HOUR_APS.multiply(time).mod(360);
minuteAngle = MINUTE_APS.multiply(time).mod(360);
secondAngle = SECOND_APS.multiply(time).mod(360);
if (minuteAngle.compareTo(secondAngle) <= 0) {
minuteAngle = minuteAngle.add(360);
}
if (hourAngle.compareTo(secondAngle) <= 0) {
hourAngle = hourAngle.add(360);
}
}
다음으로 구현할 메서드는 알람이 울리는 다음 시간으로 이동하고, 해당 시간을 반환하는 nextRing() 메서드이다.
public Fraction nextRing() {
...
}
초침이 분침과 시침을 따라 잡는 시간을 계산하기 위해서는, 각 바늘 사이의 각도와 초 당 얼마만큼의 각도를 초침이 따라잡는지를 알아야 한다.
초침이 분침과 시침을 따라잡는 속도는 각 바늘이 가지는 속도의 차이이므로 다음과 같이 나타낼 수 있다.
private static final Fraction HOUR_FOLLOW_APS = SECOND_APS.subtract(HOUR_APS);
private static final Fraction MINUTE_FOLLOW_APS = SECOND_APS.subtract(MINUTE_APS);
이를 이용하면, 초침이 분침과 시침을 따라잡는 시간은 다음과 같이 계산된다.
Fraction timeToNextHour = hourAngle.subtract(secondAngle).divide(HOUR_FOLLOW_APS);
Fraction timeToNextMinute = minuteAngle.subtract(secondAngle).divide(MINUTE_FOLLOW_APS);
이 두 시간 중 더 빠른 시간에 먼저 종이 울릴 것이므로, 다음과 같이 시간을 업데이트 해준다.
switch (timeToNextHour.compareTo(timeToNextMinute)) {
case -1: // 초침-시침 충돌
case 0: // 초침-시침-분침 충돌
time = time.add(timeToNextHour);
break;
case 1: // 초침-분침 충돌
time = time.add(timeToNextMinute);
break;
}
마지막으로 업데이트된 시간으로 바늘의 각도를 재조정하고, 시간을 반환해준다.
alignAngles();
return time;
nextRing() 메서드는 현재 시간에서 알람이 울리는지는 검사하지 않는다. 따라서 가장 처음 Clock 객체를 생성했을 때 알람이 울리는 시간인지를 판별해 줄 doesRing() 메서드도 하나 넣어준다.
public boolean doesRing() {
return secondAngle.equals(hourAngle.mod(360)) || secondAngle.equals(minuteAngle.mod(360));
}
각도를 실수형이 아니라 정수형을 갖는 분수로 표현했기 때문에 equals() 메서드를 사용해서 정확히 비교할 수 있다.
solution() 메서드
Clock 클래스가 준비되었으면 횟수를 세는 것은 쉽다.
입력받은 시간으로 Clock 객체를 초기화하고, 시간 범위 밖으로 나갈 때 까지 nextRing()을 호출하며, 그 횟수를 세주면 된다.
public int solution(int h1, int m1, int s1, int h2, int m2, int s2) {
int from = h1 * 60 * 60 + m1 * 60 + s1;
int to = h2 * 60 * 60 + m2 * 60 + s2;
Clock clock = new Clock(from);
int count = 0;
if (clock.doesRing()) {
count = 1;
}
while (true) {
double time = clock.nextRing().value();
if (time > to) return count;
count += 1;
}
}
마무리
분수와 시계의 구현을 통해 프로그래머스 PCCP 기출문제 아날로그 시계를 풀어 보았다.
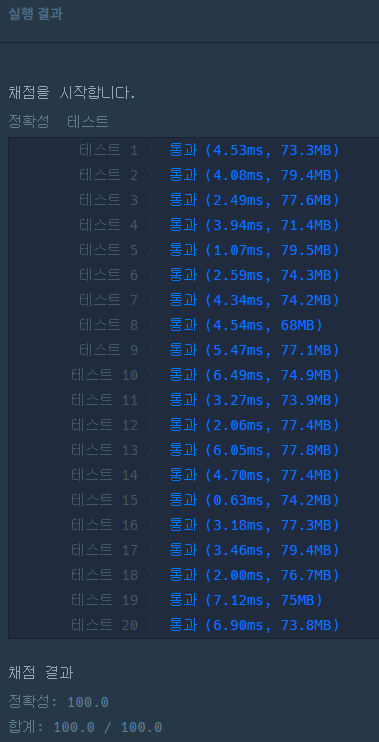
구현할 양이 많기는 해서 Lv 2는 아닌 것 같긴 하다.
내 생각이지만, Lv 2라고 매겨놓은 근거는 구현으로 푸는 것이 아니라 실제로 바늘이 언제 겹치는지는 손으로 미리 계산을 하고, 주어진 시간 범위 내에 겹치는 사건이 얼마나 발생하는지를 판별하라는 것 같다.
그런데 이 방법도 마찬가지로 초침과 분침, 초침과 시침이 얼마나 겹치는지는 계산할 수 있을 것 같은데, 초침-분침-시침이 모두 한 번에 겹치는 것이 12시 정각밖에 없다는 것을 어떻게 증명하는지를 사실 잘 모르겠다.
전체 코드
public class Solution {
private static class Fraction implements Comparable<Fraction> {
public final long numerator;
public final long denominator;
public Fraction(int value) {
this(value, 1);
}
public Fraction(long numerator, long denominator) {
long gcd = gcd(Math.abs(numerator), Math.abs(denominator));
this.numerator = numerator / gcd;
this.denominator = denominator / gcd;
}
public Fraction add(int value) {
return new Fraction(numerator + value * denominator, denominator);
}
public Fraction add(Fraction other) {
long numerator = this.numerator * other.denominator + this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction subtract(Fraction other) {
long numerator = this.numerator * other.denominator - this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction multiply(Fraction other) {
long numerator = this.numerator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction divide(Fraction other) {
return multiply(other.inverse());
}
public Fraction inverse() {
if (numerator == 0) {
throw new ArithmeticException("Cannot inverse zero.");
}
return new Fraction(denominator, numerator);
}
public Fraction mod(int value) {
return new Fraction(numerator % (value * denominator), denominator);
}
public double value() {
return (double) numerator / denominator;
}
@Override
public boolean equals(Object object) {
if (this == object) return true;
if (object == null || getClass() != object.getClass()) return false;
Fraction other = (Fraction) object;
return numerator == other.numerator && denominator == other.denominator;
}
@Override
public int compareTo(Fraction f) {
if (equals(f)) {
return 0;
} else if (value() < f.value()) {
return -1;
} else {
return 1;
}
}
private static long gcd(long a, long b) {
if (b == 0) return a;
return gcd(b, a % b);
}
}
private static class Clock {
private static final Fraction HOUR_APS = new Fraction(360, 12 * 60 * 60);
private static final Fraction MINUTE_APS = new Fraction(360, 60 * 60);
private static final Fraction SECOND_APS = new Fraction(360, 60);
private static final Fraction HOUR_FOLLOW_APS = SECOND_APS.subtract(HOUR_APS);
private static final Fraction MINUTE_FOLLOW_APS = SECOND_APS.subtract(MINUTE_APS);
private Fraction time;
private Fraction hourAngle;
private Fraction minuteAngle;
private Fraction secondAngle;
public Clock(int time) {
this.time = new Fraction(time);
alignAngles();
}
public boolean doesRing() {
return secondAngle.equals(hourAngle.mod(360)) || secondAngle.equals(minuteAngle.mod(360));
}
public Fraction nextRing() {
Fraction timeToNextHour = hourAngle.subtract(secondAngle).divide(HOUR_FOLLOW_APS);
Fraction timeToNextMinute = minuteAngle.subtract(secondAngle).divide(MINUTE_FOLLOW_APS);
switch (timeToNextHour.compareTo(timeToNextMinute)) {
case -1: // 초침-시침 충돌
case 0: // 초침-시침-분침 충돌
time = time.add(timeToNextHour);
break;
case 1: // 초침-분침 충돌
time = time.add(timeToNextMinute);
break;
}
alignAngles();
return time;
}
private void alignAngles() {
hourAngle = HOUR_APS.multiply(time).mod(360);
minuteAngle = MINUTE_APS.multiply(time).mod(360);
secondAngle = SECOND_APS.multiply(time).mod(360);
if (minuteAngle.compareTo(secondAngle) <= 0) {
minuteAngle = minuteAngle.add(360);
}
if (hourAngle.compareTo(secondAngle) <= 0) {
hourAngle = hourAngle.add(360);
}
}
}
public int solution(int h1, int m1, int s1, int h2, int m2, int s2) {
int from = h1 * 60 * 60 + m1 * 60 + s1;
int to = h2 * 60 * 60 + m2 * 60 + s2;
Clock clock = new Clock(from);
int count = 0;
if (clock.doesRing()) {
count = 1;
}
while (true) {
double time = clock.nextRing().value();
if (time > to) return count;
count += 1;
}
}
}
댓글 0
로그인이 필요합니다.
로그인

