7개 게시글

프로그래머스 > Java로 코테풀기
도넛과 막대 그래프 - Lv 2 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/258711?language=java
구현 중심의 문제로, 제시된 조건만 파악하면 쉽게 풀리는 문제였다.
문제에서 파악해야 하는 핵심 조건이 무엇이었는지를 알아보고, 이를 해결하기 위한 구현 과정을 살펴보자.
문제 풀이
문제에서는 도넛 묘양, 막대 모양, 8자 모양의 세 종류의 그래프를 제시합니다. 그리고 이 세 그래프에 속하지 않은 하나의 노드가 추가되어 모든 그래프를 연결합니다.
그래프 별 노드의 특징
먼저, 각 그래프에 속한 노드와 새로 추가한 노드의 특징을 살펴봅시다.
도넛 모양 그래프의 노드
도넛 모양 그래프의 모든 노드는 다음의 특징을 갖습니다.
하나의 나가는 간선과 하나의 들어오는 간선이 있습니다.
간선을 따라가다보면 자기 자신을 만나게 됩니다.
막대 모양 그래프의 노드
막대 그래프의 모든 노드는 다음의 특징을 갖습니다.
최대 하나의 나가는 간선과, 최대 하나의 들어오는 간선이 있습니다.
간선을 따라가다보면 막다른 노드에 도달합니다.
8자 모양 그래프의 노드
8자 모양 그래프의 모든 노드는 다음의 특징을 갖습니다.
하나의 들어오는 간선과 나가는 간선 또는 두 개의 들어오는 간선과 나가는 간선이 있습니다.
간선을 따라가다보면 두 개의 들어오는 간선과 나가는 간선을 갖는 노드를 만나게 됩니다.
새로 삽입된 노드
새로 삽입된 노드는 두 개 이상의 그래프를 연결하기 때문에 다음의 특징을 갖습니다.
들어오는 간선이 없습니다.
두 개 이상의 나가는 간선이 있습니다.
삽입된 노드 찾아 그래프 분리하기
위에서 살펴 본 노드의 특징을 활용하여 삽입된 노드를 찾아, 그래프들을 종류별로 분리할 수 있습니다.
삽입된 노드 찾기
새로 삽입된 노드의 특징 중 하나인 들어오는 간선이 없는 노드를 생각해 봅시다.
막대 모양 그래프의 시작 노드가 이러한 특징을 가질 수 있습니다. 그러나 나가는 간선이 두 개 이상이어야 한다는 점을 생각하면 이를 만족하는 노드는 새로 삽입된 노드 뿐입니다.
따라서 모든 노드를 순회하며, 들어오는 간선이 없고, 나가는 간선이 두 개 이상인 노드를 찾는다면, 해당 노드가 삽입된 노드임을 알 수 있습니다.
그래프 분리하기
삽입된 노드를 찾은 후에, 해당 노드와 연결된 간선들을 모두 끊으면 종류별로 명확히 분리된 그래프를 얻을 수 있습니다.
위 그림에서 알 수 있듯이, 삽입된 노드를 제거하면 왼쪽부터 8자 모양 그래프, 막대 모양 그래프, 8자 모양 그래프임을 쉽게 알 수 있습니다.
그래프 구분하기
그래프를 분리했으니 이제 각 그래프가 어떤 모양인지를 검사해야 합니다.
이 과정은 앞서 살펴본 노드의 특징을 활용하면 쉽게 할 수 있습니다.
임의의 한 노드로부터 출발하여 간선을 따라가다가,
막다른 노드에 도달한다면: 막대 모양 그래프
나가는 간선과 들어오는 간선의 수가 모두 2인 노드에 도달한다면: 8자 모양 그래프
출발 노드로 돌아온다면: 도넛 모양 그래프
여기서 주의할 점은, 8자 모양 그래프에 대한 검사를 도넛 모양 그래프 검사보다 우선 해야 한다는 것입니다.
8자 모양 그래프도 한 노드로부터 간선을 따라가다보면 자기 자신이 나오게 됩니다. 하지만 그 이전에 8자 모양 그래프의 중심 노드를 거쳐야 하기 때문에 이를 우선 검사하여 8자 모양 그래프와 도넛 모양 그래프를 구분합니다.
코드
이를 코드로 구현하면 다음과 같습니다.
import java.util.*;
import java.util.function.Function;
class Solution {
enum NodeType {
DONUT,
LINEAR,
EIGHT,
}
static class Node {
List<Node> outs = new ArrayList<>();
List<Node> ins = new ArrayList<>();
NodeType type;
}
private static Map<Integer, Node> constructNodes(int[][] edges) {
Map<Integer, Node> nodes = new HashMap<>();
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
if (!nodes.containsKey(u)) nodes.put(u, new Node());
if (!nodes.containsKey(v)) nodes.put(v, new Node());
Node from = nodes.get(u);
Node to = nodes.get(v);
from.outs.add(to);
to.ins.add(from);
}
return nodes;
}
private static int findInsertedNodeKey(Map<Integer, Node> nodes) {
for (int key : nodes.keySet()) {
Node node = nodes.get(key);
if (node.ins.size() == 0 && node.outs.size() >= 2) {
return key;
}
}
// Unreachable
return -1;
}
private static int removeInsertedNode(Map<Integer, Node> nodes) {
int insertedKey = findInsertedNodeKey(nodes);
Node inserted = nodes.remove(insertedKey);
for (Node node : inserted.ins) {
node.outs.remove(inserted);
}
for (Node node : inserted.outs) {
node.ins.remove(inserted);
}
return insertedKey;
}
private static Node getUnvisitedNext(Node node, List<Node> direction) {
for (Node next : direction) {
if (next.type == null) return next;
}
return null;
}
private static void mark(Node node, NodeType type, Function<Node, List<Node>> getDirection) {
do {
node.type = type;
node = getUnvisitedNext(node, getDirection.apply(node));
} while (node != null);
}
private static NodeType check(Node node) {
Node initial = node;
while (true) {
if (node.outs.size() == 0) {
mark(node, NodeType.LINEAR, n -> n.ins);
return NodeType.LINEAR;
} else if (node.ins.size() == 2 && node.outs.size() == 2) {
mark(getUnvisitedNext(node, node.outs), NodeType.EIGHT, n -> n.outs);
return NodeType.EIGHT;
}
node = getUnvisitedNext(node, node.outs);
if (node == null) {
// Unreachable
break;
}
if (node == initial) {
mark(node, NodeType.DONUT, n -> n.outs);
return NodeType.DONUT;
}
};
return null;
}
public int[] solution(int[][] edges) {
Map<Integer, Node> nodes = constructNodes(edges);
int insertedKey = removeInsertedNode(nodes);
int donut = 0;
int linear = 0;
int eight = 0;
for (Node node : nodes.values()) {
if (node.type != null) continue;
switch (check(node)) {
case LINEAR:
linear += 1;
break;
case EIGHT:
eight += 1;
break;
case DONUT:
donut += 1;
break;
}
}
return new int[] { insertedKey, donut, linear, eight };
}
}
02024. 08. 23.

프로그래머스 > Java로 코테풀기
안티세포 - Lv 4 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/86054
프로그래머스에서는 가끔씩 월간 코드 챌린지라는 대회를 한다.
지금까지 총 3회를 했는데, 이 문제는 그 중 마지막인 월간 코드 챌린지 시즌 3에 출제된 문제이다.
DP인 것 같다는 생각이 들긴 했지만 조금 특이한 형태의 DP라 시간이 좀 걸렸다. 시간 복잡도를 활용해 풀이에 접근하는 방식을 한 번 살펴보도록 하자.
문제 풀이
입출력을 다루는 것은 따로 다루지 않고, 안티 세포 배열 b에 대해서 만들 수 있는 서로 다른 배열 c의 개수를 구하는 것만 다루겠습니다.
c를 구해야 할까? 문제 단순화 하기
이 문제의 핵심은 c를 과연 구해야 하는지 여부를 파악하는 데 있습니다.
예를 들어서, 문제에서 주어진 안티 세포인 (1)(1)(1)(1)이 있습니다.
이 안티 세포를 (1, 1)(1, 1)과 같은 형태로 합치는 c는 몇 개가 존재할까요?
[1, 3] 하나밖에 없습니다.
또, (1)(1)(1, 1)을 만들기 위한 c는 몇 개일까요?
[3] 하나입니다.
감이 오시나요?
안티 세포가 합쳐질 수 있는 모든 경우의 수에 대해서,
해당 경우의 수를 만들어낼 수 있는 c는 유일합니다.
반대로, 서로 다른 배열 c는 다르게 합쳐진 안티 세포 결과를 만들어 내게 됩니다.
이는 다음의 두 특성 때문에 성립하게 됩니다.
세포가 합쳐질 때, 두 세포는 같은 값을 가지고 있다.
b의 인덱스 i는 항상 증가하는 방향으로 이동한다.
이에 따라, 세포가 합쳐질 때, c에 기록되는 i는 합쳐지는 세포의 마지막 인덱스가 되게 됩니다.
즉 같은 형태의 합쳐진 세포를 만들기 위해서 해당 세포 내의 다른 인덱스가 기록되는 일이 없다는 뜻이고,
결과 모양이 같으면 c 또한 같다는 결론에 이르르게 됩니다.
이 내용을 파악했다면, 문제를 단순화할 수 있습니다.
이제 문제는 가능한 c의 개수를 구하는 것이 아니라, 안티 세포가 합쳐질 수 있는 경우의 수를 구하는 문제가 됩니다.
시간 복잡도로 해법 추정하기
문제에서 a의 길이가 최대 200,000이므로, b의 길이의 최대도 200,000이 됩니다.
b의 길이를 N이라고 합시다.
배열의 원소를 적어도 한 번씩은 방문해야 하기에, O(N)은 필연적으로 소요됩니다.
이제 원소를 방문할 때마다 얼마만큼의 시간 복잡도를 소요할 수 있는지를 생각해 봅시다.
N의 최대가 200,000인만큼 한 연산에 O(N)이 걸리게 된다면 전체 시간 복잡도가 O(N²)이 되어 시간 초과입니다.
한 번의 연산 당 가능한 시간 복잡도는 O(logN) 혹은 O(1)이 됩니다.
O(logN) 가능성 살펴보기
저번 포스트, 행렬과 연산 - Lv 4 문제 풀이에서 언급했듯이, O(logN)은 특별한 시간 복잡도입니다.
이 문제에 이를 적용할만한 내용이 있을까요?
행렬과 연산 문제와는 달리, 이번 문제에는 그런 내용이 있습니다.
바로 "같은 값을 가지고 있는 안티 세포만 합쳐질 수 있다"라는 점 때문입니다.
안티 세포가 여러 번 합쳐지는 경우를 생각해 봅시다.
처음엔 1 두 개가 합쳐져 2가 만들어집니다.
그 다음엔 2 두 개가 합쳐저 4가 만들어집니다.
그 다음엔 4 두 개가 합쳐저 8이 만들어집니다.
그 다음엔 8 두 개가 합쳐저 16이 만들어집니다.
이처럼 합쳐지는 안티 세포의 숫자는 계속 두 배씩 커지게 됩니다.
다음과 같은 배열을 생각해 봅시다.
[64, 32, 16, 8, 4, 2, 1, 1]
가장 오른쪽에 있는 1을 가능한 만큼 합치는 경우에 모든 원소가 합쳐집니다.
이는 O(N)번이라고 할 수 있을 것입니다.
그러면 연산에는 최대 O(N)이 걸리는 것이 아닐까요?
문제의 조건 중 원소의 값은 10^9보다 작거나 같다는 점이 있습니다.
안티 세포가 합쳐질 수 있는 가장 큰 수는 10^9인 것입니다.
그리고 이를 만들기 위해서는 최대 log_2(10^9)인 약 30번의 합 밖에 소요되지 않습니다.
즉, log는 배열의 길이에 적용되는 것이 아니라, 배열 원소의 값에 적용되는 것이었던 것을 알 수 있습니다.
10^9는 배열 b의 최댓값이므로 log_2(max(b))라고 표기할 수 있습니다.
따라서 전체 시간 복잡도는 O(n log(max(b))가 됩니다.
이는 n과 max(b)의 최댓값을 넣어보면 약 600만의 수치로 계산되어, 충분한 시간 복잡도입니다.
원소 당 연산 생각하기
위에서 log의 가능성을 확인하였습니다.
log가 배열 원소의 값에 적용이 된다는 것은, 해당 원소가 합쳐질 수 있는 횟수가 최대 log(max(b)) 번이라는 의미입니다.
연산의 시간 복잡도를 O(log(max(b))로 유지하기 위해서는 세포를 합쳐서 원하는 합을 만드는 경우의 수를 구하는 시간 복잡도는 상수 시간이어야 합니다. 그래야 이를 log(max(b)) 번 반복해도 전체 시간 복잡도가 O(log(max(b))가 되기 때문입니다.
즉, 각 원소 별로 만들 수 있는 합에 대해서, 각 경우의 수를 가지고 있어야 합니다.
예를 들어 [1, 1, 1, 1]의 경우에는 다음과 같은 데이터를 생성해낼 수 있어야 합니다.
b[0] = 1 b[1] = 1 b[2] = 1 b[3] = 1
합:1, 경우의 수: 1 합:1, 경우의 수: 1 합:1, 경우의 수: 2 합:1, 경우의 수: 3
합:2, 경우의 수: 1 합:2, 경우의 수: 1 합:2, 경우의 수: 2
합:4, 경우의 수: 1
경우의 수 구하기
각 합을 만들어내는 경우의 수를 구하기 위해, 우선 위의 표를 어떻게 만들 수 있는지 합 별로 하나씩 살펴봅시다.
1. 합 1을 만드는 경우
이 경우는 해당 원소만으로 안티 세포의 합을 만들어낼 수 있습니다.
따라서 직전 원소로 만들 수 있는 모든 경우의 수가 해당 원소로 합 1을 만드는 경우의 수가 됩니다.
예를 들어, 위 표에서 마지막 1로 합 1을 만드는 경우의 수를 구하기 위해서는 직전 1인 세 번째 1로 만들 수 있는 모든 경우의 수를 더해주면 됩니다.
2. 합 2를 만드는 경우
이 경우도 위와 비슷하게 처리할 수 있습니다.
합을 2를 만들기 위해선 직전 안티 세포와 합쳐야 합니다.
이 때 경우의 수는 합쳐진 안티 세포들을 제외하고, 그 앞에 있는 안티 세포로 만들 수 있는 경우의 수가 됩니다.
예를 들어, 마지막 1로 합 2를 만드는 경우의 수는 직전에 있는 1로 1을 만드는 경우의 수와 같습니다.
3. 합 4를 만드는 경우
합 4를 만들기 위해서는 합 2를 두 개 합쳐야 합니다.
따라서 이 경우의 수는 현재 검사하는 원소로 2를 만들 수 있는 경우의 수와,
이 안티 세포 직전의 원소를 포함해 2를 만들 수 있는 경우의 수를 곱한 것이 됩니다.
예를 들어, 마지막 1로 합 4를 만드는 경우는,
마지막 1로 합 2를 만드는 경우의 수인 1과
여기에 포함되지 않으면서, 직전 원소인 두 번째 1로 합 2를 만드는 경우의 수인 1을 곱하여
1이 그 경우의 수가 됩니다.
논리 일반화하기
여기까지 왔으면 합 2, 4를 만들어낸 논리를 다음과 같이 일반화 할 수 있습니다.
합 1을 만드는 경우의 수는 쉽게 구할 수 있으므로 제외합니다.
합 n을 만드는 경우의 수 =
해당 원소로 합 n/2를 만드는 경우의 수 *
안티 세포 직전 원소로 합 n/2를 만드는 경우의 수
합쳐진 안티 세포 직전 원소 구하기
해당 원소로 합 n/2를 만드는 경우의 수는 재귀적으로 쉽게 구할 수 있습니다.
그런데 안티 세포 직전 원소는 어떻게 구할 수 있을까요?
이를 구하기 위해서는 원소별로 합과 경우의 수 외에 안티 세포의 시작 인덱스를 함께 넣어주면 됩니다.
즉, 이제 다음과 같이 데이터를 만들어 주면 됩니다.
전체 코드
위 내용을 종합하면, 다음과 같이 문제를 풀 수 있습니다.
import java.util.*;
public class Solution {
private static final int DIV = 1_000_000_007;
private static int sum(int a, int b) {
long sum = (long) a + b;
return (int) (sum % DIV);
}
private static class Count {
final long sum;
final int count;
final int offset;
public Count(long sum, int count, int offset) {
this.sum = sum;
this.count = count;
this.offset = offset;
}
}
private int solve(int[] b) {
List<Map<Long, Count>> counts = new ArrayList<>(b.length);
for (int i = 0; i < b.length; i++) {
Map<Long, Count> map = new HashMap<>();
counts.add(map);
long targetSum = b[i];
if (i == 0) {
map.put(targetSum, new Count(targetSum, 1, i));
} else {
map.put(
targetSum,
new Count(
targetSum,
counts.get(i - 1).values().stream()
.mapToInt(c -> c.count)
.reduce(Solution::sum)
.orElse(0),
i));
}
while (true) {
targetSum *= 2;
Count lastCount = map.get(targetSum / 2);
int prevOffset = lastCount.offset - 1;
if (prevOffset < 0) break;
Map<Long, Count> prevMap = counts.get(prevOffset);
if (!prevMap.containsKey(targetSum / 2)) break;
Count count = prevMap.get(targetSum / 2);
map.put(targetSum, new Count(targetSum, count.count, count.offset));
}
}
return counts.get(counts.size() - 1).values().stream()
.mapToInt(c -> c.count)
.reduce(Solution::sum)
.orElse(0);
}
public int[] solution(int[] a, int[] s) {
int[] answer = new int[s.length];
int offset = 0;
for (int i = 0; i < answer.length; i++) {
answer[i] = solve(Arrays.copyOfRange(a, offset, offset + s[i]));
offset += s[i];
}
return answer;
}
}
02024. 06. 22.

프로그래머스 > Java로 코테풀기
행렬과 연산 - Lv 4 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/118670
정확성과 효율성 테스트가 같이 있는 문제이다.
코딩 테스트에서 이런 문제를 만나게 되면 효율성 테스트의 조건을 먼저 보아야 한다.
효율성 테스트를 해결할 수 있는 풀이는 정확성 테스트도 해결할 수 있지만,
정확성 테스트를 해결할 수 있는 풀이는 효율성 테스트를 통과하지 못할 수 있기 때문이다.
만약 처음부터 정확성 테스트의 조건을 해결하는 풀이를 고민한다면,
한 문제를 두 번 풀어야 하는 상황이 발생할 수 도 있다.
따라서 효율성 테스트를 먼저 고민하고, 정 모르겠다 싶으면 정확성 테스트의 조건을 보도록 하자.
이번 포스트에서는 효율성 테스트에 대한 풀이만 다루겠다.
문제 풀이
제한 사항으로 시간 복잡도 유추하기
문제의 제한 사항을 살펴봄으로써 문제가 원하는 해답의 시간 복잡도를 유추해 봅시다.
제한 사항에 따르면 행렬의 크기는 최대 100,000입니다. 이를 N이라고 합시다.
또, 연산의 개수도 최대 100,000입니다. 이를 M이라고 합시다.
만약 하나의 연산에 대해 행렬 전체를 업데이트 해야 한다면 연산 한 번에 O(N)의 시간 복잡도가 소요되어, 전체 시간 복잡도는 O(MN)이 됩니다.
이는 최대 100억에 해당하는 수치로, 시간 복잡도 제한인 1억을 훌쩍 넘겨버립니다.
operations를 순회하며 연산을 하나씩 적용하는 것은 줄일 수 없는 시간 복잡도입니다.
O(M)은 이미 정해져있고, 여기에 곱해지는 시간 복잡도인 연산 하나당 소요되는 시간 복잡도를 줄여야 한다는 의미입니다.
M 자체로 이미 10만이기 때문에 연산 하나 당 소요되는 시간 복잡도를 O(1), 혹은 적어도 O(logN)으로 줄여야 합니다.
연산에 대한 시간 복잡도 생각하기
O(logN)은 특별한 시간 복잡도입니다.
O(logN)이라는 시간 복잡도를 만들어 내는 접근법들은 대부분 그 유형이 정해져 있습니다.
트리, 이분 탐색, 분할 정복 등이 있는데, 이들 모두 배열을 회전시키는 연산과는 딱히 연결성이 없어 보입니다.
따라서 연산에 상수 시간인 O(1)이 소요되는 것이 가장 그럴듯합니다.
시간 복잡도 기반으로 연산 접근하기
연산에 상수 시간이 소요된다면 아주 간단한 연산으로 해결된다는 의미입니다.
ShiftRow의 경우 숫자가 섞이는 것이 아니기 때문에 행렬에서 가장 윗 행이 어디인지를 추적하는 것으로 상수 시간 안에 해결이 됩니다.
문제는 Rotate입니다. 숫자들의 순서가 바뀌게 되므로 실제 숫자들이 어떻게 움직이는지를 추적해야 합니다.
이를 어떻게 상수 시간 안에 해결할 수 있을까요?
Rotate 연산
문제에서 주어진 회전 연산을 생각해 보면, 행렬의 겉에서만 숫자들이 회전합니다.
즉, 가장자리를 상하좌우 4개로 나누어 생각해보면, 한쪽 가장자리에서 빠진 숫자는 다른 가장자리로 들어가게 됩니다.
이는 LinkedList로 해결할 수 있습니다.
행렬의 상하좌우를 관리하는 LinkedList를 만들어, 회전 연산 때 원소 하나를 제거하고 다른 리스트로 넣어주는 방식입니다.
LinkedList는 가장 앞 원소와 가장 뒤에 있는 원소의 추가/삭제 연산에 대한 시간 복잡도가 O(1)이므로 상수 시간 안에 해결할 수 있습니다.
rotate 연산을 실제로 상수 시간 안에 해결할 수 있게 된 것입니다.
그런데 이 LinkedList를 구성하는 방법에는 다음과 같이 여러 가지가 있습니다.
이 중 어떤 방식으로 리스트를 구성해야 할까요?
Rotate 연산만 생각하면 어떤 방식을 채택하든 큰 상관이 없습니다.
그렇다면 ShiftRow 연산까지 생각해 봅시다.
ShiftRow 연산
앞에서 배열의 행 인덱스를 이용해 상수 시간 안에 연산을 해결했는데,
Rotate 연산을 해결하려다 보니 배열의 실제 구성이 바뀌게 되었습니다.
ShiftRow 연산은 모든 숫자들을 한 칸씩 아래로 내립니다.
이를 쉽게 구현하기 위해서는 LinkedList가 열 방향으로, 즉 세로로 구성되어 있어야 합니다.
이렇게 구현해 놓게 되면 ShiftRow 연산이 발생했을 시에 가장 왼쪽과 오른쪽 LinkedList는 마지막 숫자를 빼서, 자신의 가장 앞에 넣어주면 됩니다.
가운데 남은 숫자들의 경우 ShiftRow 연산이 발생하면 가장자리로 갈 수 있게 됩니다.
따라서 Rotate 연산에 포함될 경우를 대비해 미리 다음과 같이 LinkedList에 넣어줍니다.
이제 ShiftRow 연산은 가운데에 있는 LinkedList 자체를 한 칸씩 내려주면 됩니다.
이를 위해 가운데 LinkedList 전체를 또 다른 LinkedList로 감싸줍니다.
ShiftRow와 Rotate 연산을 모두 상수 시간 안에 처리할 수 있기 때문에, 연산을 처리하는 시간 복잡도는 O(M)이 됩니다.
전체 시간 복잡도는 행렬의 원소를 한 번씩 읽고 쓰는 O(N)과 연산을 처리하는 O(M) 중 더 큰 시간 복잡도가 됩니다.
이는 O(N + M) 으로 표기할 수 있습니다.
LinkedList 구성 살펴보기
위에서 구성한 LinkedList를 이용하면 Rotate와 ShiftRow 연산을 상수 시간 안에 할 수 있습니다.
Rotate 연산에는 다음의 LinkedList들이 관여합니다.
ShiftRow 연산에는 다음의 LinkedList들이 관여합니다.
구현하기
Matrix 클래스 만들기
행렬에 관련된 연산을 처리하기 위한 클래스 Matrix를 다음과 같이 작성해 줍니다.
private static class Matrix {
public final int w;
public final int h;
Matrix(int[][] rc) {
w = rc[0].length;
h = rc.length;
}
}
LinkedList 구성하기
Matrix 클래스는 이차원 배열 rc를 생성자에 입력받아, 위에서 살펴본 LinkedList로 구성해주어야 합니다.
이를 위해 왼쪽 left, 오른쪽 right, 그리고 가운데의 LinkedList를 가리키는 body를 다음과 같이 선언해 줍니다.
private final LinkedList<Integer> left = new LinkedList<>();
private final LinkedList<Integer> right = new LinkedList<>();
private final LinkedList<LinkedList<Integer>> body = new LinkedList<>();
이 세 LinkedList들은 생성자에서 다음과 같이 채워줄 수 있습니다.
for (int i = 0; i < h; i++) {
LinkedList<Integer> bodyRow = new LinkedList<>();
for (int j = 0; j < w; j++) {
if (j == 0) {
left.add(rc[i][j]);
} else if (j == w - 1) {
right.add(rc[i][j]);
} else {
bodyRow.add(rc[i][j]);
}
}
body.add(bodyRow);
}
ShiftRow 연산
ShiftRow는 세 LinkedList의 가장 마지막 원소를 제거하고, 가장 앞 원소에 추가해 주는 연산을 해주는 연산입니다.
void shiftRow() {
left.addFirst(left.removeLast());
right.addFirst(right.removeLast());
body.addFirst(body.removeLast());
}
LinkedList의 addFirst(), removeLast() 연산은 상수 시간이므로, shiftRow() 메서드 또한 상수 시간이 걸림을 다시 한번 확인할 수 있습니다.
Rotate 연산
Rotate는 가장자리에 있는 LinkedList들끼리 원소를 하나씩 밀어주는 연산입니다.
void rotate() {
LinkedList<Integer> firstBodyRow = body.getFirst();
LinkedList<Integer> lastBodyRow = body.getLast();
firstBodyRow.addFirst(left.removeFirst());
lastBodyRow.addLast(right.removeLast());
right.addFirst(firstBodyRow.removeLast());
left.addLast(lastBodyRow.removeFirst());
}
마찬가지로 모든 메서드가 상수 시간을 가져, rotate() 연산 또한 상수 시간임을 확인할 수 있습니다.
여기에서 주의해야 할 점이, left, right에서 bodyRow들로 원소를 보내는 작업의 순서가 더 빨라야 한다는 점입니다.
bodyRow에서 left, right으로 원소를 보내는 작업을 먼저 해주게 된다면, 행렬의 가로길이가 2인 경우 bodyRow는 빈 LinkedList가 되는데, 이때 NoSuchElementException이 발생하게 됩니다.
이차원 배열 변환
마지막으로, 연산이 종료된 행렬을 다시 이차원 배열로 변환시켜주어야 합니다.
이는 build() 메서드에 다음과 같이 작성합니다.
int[][] build() {
int[][] matrix = new int[h][w];
Iterator<Integer> leftIterator = left.iterator();
Iterator<Integer> rightIterator = right.iterator();
Iterator<LinkedList<Integer>> bodyIterator = body.iterator();
for (int i = 0; i < h; i++) {
matrix[i][0] = leftIterator.next();
matrix[i][w - 1] = rightIterator.next();
Iterator<Integer> bodyRowIterator = bodyIterator.next().iterator();
for (int j = 1; j < w - 1; j++) {
matrix[i][j] = bodyRowIterator.next();
}
}
return matrix;
}
이 부분을 작성할 때, get()을 사용하여 LinkedList의 원소에 접근하지 않도록 주의해야 합니다.
LinkedList는 ArrayList와 달리, get()에 O(N)의 시간 복잡도가 소요되기 때문입니다.
어차피 LinkedList의 원소들을 순차적으로 접근하므로 Iterator를 이용하여 원소 참조에 불필요한 시간을 소요하지 않도록 합니다.
solution() 메서드
solution 메서드에서는 주어진 rc를 이용해 Matrix를 생성하고,
주어진 연산을 모두 적용해 준 다음,
이차원 배열로 변환하여 반환합니다.
public int[][] solution(int[][] rc, String[] operations) {
Matrix matrix = new Matrix(rc);
for (String operation : operations) {
switch (operation) {
case "ShiftRow":
matrix.shiftRow();
break;
case "Rotate":
matrix.rotate();
break;
}
}
return matrix.build();
}
전체 코드
import java.util.Iterator;
import java.util.LinkedList;
public class Solution {
private static class Matrix {
public final int w;
public final int h;
private final LinkedList<Integer> left = new LinkedList<>();
private final LinkedList<Integer> right = new LinkedList<>();
private final LinkedList<LinkedList<Integer>> body = new LinkedList<>();
Matrix(int[][] rc) {
w = rc[0].length;
h = rc.length;
for (int i = 0; i < h; i++) {
LinkedList<Integer> bodyRow = new LinkedList<>();
for (int j = 0; j < w; j++) {
if (j == 0) {
left.add(rc[i][j]);
} else if (j == w - 1) {
right.add(rc[i][j]);
} else {
bodyRow.add(rc[i][j]);
}
}
body.add(bodyRow);
}
}
void shiftRow() {
left.addFirst(left.removeLast());
right.addFirst(right.removeLast());
body.addFirst(body.removeLast());
}
void rotate() {
LinkedList<Integer> firstBodyRow = body.getFirst();
LinkedList<Integer> lastBodyRow = body.getLast();
firstBodyRow.addFirst(left.removeFirst());
lastBodyRow.addLast(right.removeLast());
right.addFirst(firstBodyRow.removeLast());
left.addLast(lastBodyRow.removeFirst());
}
int[][] build() {
int[][] matrix = new int[h][w];
Iterator<Integer> leftIterator = left.iterator();
Iterator<Integer> rightIterator = right.iterator();
Iterator<LinkedList<Integer>> bodyIterator = body.iterator();
for (int i = 0; i < h; i++) {
matrix[i][0] = leftIterator.next();
matrix[i][w - 1] = rightIterator.next();
Iterator<Integer> bodyRowIterator = bodyIterator.next().iterator();
for (int j = 1; j < w - 1; j++) {
matrix[i][j] = bodyRowIterator.next();
}
}
return matrix;
}
}
public int[][] solution(int[][] rc, String[] operations) {
Matrix matrix = new Matrix(rc);
for (String operation : operations) {
switch (operation) {
case "ShiftRow":
matrix.shiftRow();
break;
case "Rotate":
matrix.rotate();
break;
}
}
return matrix.build();
}
}
02024. 06. 20.

프로그래머스 > Java로 코테풀기
쌍둥이 빌딩 숲 - Lv 4 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/140105
처음 그림을 봤을 때 생긴 건 스택으로 푸는 히스토그램 문제랑 비슷하게 생겼다고 생각했다.
제목에 쌍둥이가 들어가서 짝을 찾아야 하나 하는 생각이 들어서 그런 것도 있는 것 같다.
하지만 문제를 읽어보니 전혀 스택과는 관련 없어보였다. 오히려 처음에 히스토그램 문제를 접했을 때 떠올리는 점화식을 활용한 재귀적 접근으로 풀리는 문제였다.
문제 풀이
같은 높이를 가지는 빌딩 사이에는 그보다 높은 빌딩이 존재하지 않습니다.
이 조건에 집중해 봅시다.
이것에 따르면 빌딩들이 배치된 상태에서 가장 작은 빌딩을 배치하려고 할 때,
가장 작은 빌딩의 쌍은 항상 붙어 있어야 한다는 것을 알 수 있습니다.
예를 들어, 다음과 같이 빌딩이 배치되어 있습니다.
가장 작은 노란색 빌딩 쌍을 추가한다고 생각해봅시다.
다음의 경우는 불가능합니다.
반면, 다음과 같이 노란색 빌딩 쌍을 붙인다면, 이미 있는 건물 사이에 어떤 곳에 배치하던 가능한 경우가 됩니다.
위의 그림에서 알 수 있는 중요한 점은 노란색 건물을 가장 앞에 배치하는 경우가 아니면, 노란색 건물은 보이지 않는다는 것입니다.
이를 활용하면 문제를 풀기 위한 점화식을 세울 수 있습니다.
다음과 같이 상태를 정의해봅시다.
(n, c): n개의 건물 쌍을 배치했을 때, c개의 건물이 보이는 경우의 수
- (0, 0) = 1
- (0, c) = 0
- (n, 0) = 0
- c > n인 경우 (n, c) = 0
n개의 건물 쌍을 배치 하기 위해서는:
n-1개의 건물 쌍을 배치
가장 작은 건물 쌍을 어디에 배치할 것인지 정하기
가장 작은 건물 쌍의 위치와 이 건물 쌍을 제외한 건물들의 배치가 다르기 때문에 중복이 발생하지 않습니다.
또, 가장 작은 건물은 어떤 경우이던 항상 존재하므로 누락이 발생하지도 않습니다.
가장 작은 건물을 맨 앞에 배치하는 경우:
1개의 경우의 수가 있습니다.
보이는 건물의 수가 1개 늘어납니다.
가장 작은 건물을 다른 건물 사이에 배치하는 경우:
2(n-1)개의 경우의 수가 있습니다.
보이는 건물의 수는 늘어나지 않습니다.
이를 이용하면, n개의 건물을 배치했을 때 c개의 건물이 보이기 위해서는, 이전 단계인 n-1개의 건물을 배치했을 때:
c-1개의 건물이 보이는 경우하나의 건물이 더 보여야 하므로 가장 작은 건물을 맨 앞에 배치
1개의 경우의 수
c개의 건물이 보이는 경우보이는 건물의 수가 늘어나지 않아야 하므로 다른 건물 사이에 배치
2(n-1)개의 경우의 수
즉, 다음과 같이 점화식을 쓸 수 있습니다.
(n, c) = (n-1, c-1) + (n-1, c) * 2(n-1)
시간 복잡도
하나의 상태를 계산할 때 별도의 반복이 필요하지 않습니다.
따라서 상태의 개수에 해당하는 시간 복잡도가 소요게 되어 O(nc)의 시간 복잡도를 갖습니다.
문제의 조건에 따라 n과 c의 최댓값은 100이므로 매우 넉넉한 시간 복잡도입니다.
최댓값 조건이 1000이어도 충분한 시간 복잡도가 됩니다.
전체 코드
import java.util.Arrays;
public class Solution {
private static final int DIV = 1_000_000_007;
private static final int[][] mem = new int[101][101];
static {
for (int[] row : mem) {
Arrays.fill(row, -1);
}
for (int n = 0; n <= 100; n++) {
mem[n][0] = 0;
for (int c = n + 1; c <= 100; c++) {
mem[n][c] = 0;
}
}
mem[0][0] = 1;
}
public int solution(int n, int count) {
if (mem[n][count] != -1) return mem[n][count];
long sum = solution(n - 1, count - 1);
sum += (long) solution(n - 1, count) * 2 * (n - 1);
return mem[n][count] = (int) (sum % DIV);
}
}
원래 static 블럭을 잘 사용하지 않는데, 이번 문제에서는 solution() 메서드 자체를 재귀시킬 수 있어서 사용했습니다.
02024. 06. 19.
프로그래머스 > Java로 코테풀기
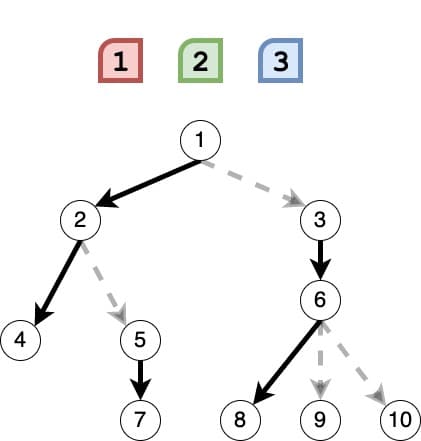
1, 2, 3 떨어뜨리기 - Lv. 4 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/150364
2023 카카오 블라인드의 문제이다.
트리 그림이 그려져 있지만 구현의 비중이 더 높았던 것 같다.
[취업과 이직을 위한 프로그래머스 문제 풀이 전략: 자바편]을 집필할 때 정말 신경 썼던 것이 가독성이다.
이 문제처럼 구현 비중이 높은 문제들을 특히 가독성을 생각하며 코드를 작성해야 한다.
" 읽기 쉬운 코드는 로직에만 집중할 수 있으므로 이해하기 쉽고, 실수가 있어도 쉽게 잡아낼 수 있습니다.
:: - [취업과 이직을 위한 프로그래머스 문제 풀이 전략: 자바편] 中 - ::
구현 문제의 풀이 코드는 문제에서 요구하는 로직을 다뤄야 한다.
로직이 제대로 구현되었는지를 파악하고, 실수를 줄이기 위해서는 가독성은 필수 요소이다.
문제 풀기
이 문제는 알고리즘적으로 설명할 것은 크게 없습니다. 풀이도 아주 직관적입니다.
문제의 조건을 만족하는 트리 구현
어떤 순서로 리프 노드들에 숫자가 떨어지는지 구하기
target을 만들 수 있는 방법이 있는지 검사하기
알고리즘보다는 구현에 초점이 맞춰진 문제인 만큼, 시간 복잡도를 따져보는 것은 의미가 없을 듯 하여 구현에 대한 내용만 다루겠습니다.
트리 구성하기
문제에서 edges가 이차원 배열로 주어지고, 이를 이용해 트리를 구성해야 합니다.
트리는 노드로 구성되어 있습니다.
가장 단순한 노드는 다음의 멤버 필드를 가지고 있을 것입니다.
index: 자신의 노드 번호.
children: 자식 노드들 리스트.
또, 다음의 메서드를 가집니다.
addChild(): 자식 노드 추가.
isLeaf(): 리프 노드인지 검사.
여기까지 코드
private static class Node {
public final int index;
private final List<Node> children = new ArrayList<>();
Node(int index) {
this.index = index;
}
void addChild(Node child) {
children.add(child);
}
void sortChild() {
children.sort(Comparator.comparingInt(n -> n.index));
}
private boolean isLeaf() {
return children.isEmpty();
}
}
이 문제의 노드는 조금 특별합니다.
여러 자식 노드들 중 하나의 자식만 참조할 수 있고,
한 번 참조한 이후에는 다음 자식 노드를 참조하게 됩니다.
또, 이 순서는 자식 노드의 index 순서를 따릅니다.
이에 따라 다음의 메서드를 정의합니다.
trigger(): 연결된 노드를 따라 내려갔을 때 도착하는 리프 노드를 반환. 한 번 호출 후에는 다음 자식 노드를 참조.
sortChild(): 등록된 자식 노드들을 index 순으로 정렬.
이 부분에 해당하는 코드
private int childIndex = 0;
Node trigger() {
if (isLeaf()) {
return this;
}
Node leaf = children.get(childIndex).trigger();
childIndex = (childIndex + 1) % children.size();
return leaf;
}
void sortChild() {
children.sort(Comparator.comparingInt(n -> n.index));
}
완성된 Node 클래스는 다음과 같습니다.
private static class Node {
public final int index;
private final List<Node> children = new ArrayList<>();
private int childIndex = 0;
Node(int index) {
this.index = index;
}
Node trigger() {
if (isLeaf()) {
return this;
}
Node leaf = children.get(childIndex).trigger();
childIndex = (childIndex + 1) % children.size();
return leaf;
}
void addChild(Node child) {
children.add(child);
}
void sortChild() {
children.sort(Comparator.comparingInt(n -> n.index));
}
private boolean isLeaf() {
return children.isEmpty();
}
}
문제에서 입력 받은 edges를 이용하여 Node로 구성된 트리를 만들어 주는 constructTree() 메서드를 다음과 같이 정의해 줍니다.
private static Node constructTree(int[][] edges) {
Node[] nodes = new Node[edges.length + 1];
for (int i = 0; i < nodes.length; i++) {
nodes[i] = new Node(i);
}
for (int[] edge : edges) {
nodes[edge[0] - 1].addChild(nodes[edge[1] - 1]);
}
for (Node node : nodes) {
if (node == null) continue;
node.sortChild();
}
return nodes[0];
}
이렇게 구성된 트리를 이용하면 숫자가 떨어지는 리프 노드의 순서를 구할 수 있습니다.
target 숫자를 만들 수 있는지 검사
리프 노드에 떨어지는 횟수가 너무 적거나 너무 많다면 해당 리프 노드에서 원하는 숫자를 만들 수 없습니다.
이를 관리하기 위해 노드별로 목표하는 target 숫자를 만드는 클래스 Target을 만들어줍니다.
Target 클래스는 다음과 같은 멤버 필드를 가지게 됩니다.
value: 해당 노드의 target 숫자
tries: 해당 노드에 숫자가 떨어진 횟수
이 두 값을 이용하면 다음의 연산을 할 수 있습니다.
addTry(): 해당 노드에 숫자가 떨어진 횟수 1 증가
isNotEnough(): 아직 target 숫자를 만들기에는 해당 노드에 숫자가 떨어진 횟수가 부족
떨어진 횟수 x 3이 해당 횟수로 만들 수 있는 최대 숫자
didTooManyTries(): target 숫자를 만들기에는 해당 노드에 숫자가 너무 많이 떨어짐
떨어진 횟수 자체가 해당 횟수로 만들 수 있는 최소 숫자
isSolved(): target 숫자를 만들 수 있을 만큼 해당 노드에 숫자가 떨어짐
여기까지 코드
private static class Target {
public final int value;
private int tries = 0;
Target(int value) {
this.value = value;
}
void addTry() {
tries += 1;
}
boolean isNotEnough() {
return value > tries * 3;
}
boolean didTooManyTries() {
return value < tries;
}
boolean isSolved() {
return !isNotEnough() && !didTooManyTries();
}
}
target 숫자를 만들기 위해 떨어뜨려야 하는 숫자 순서 구하기
위의 Target 클래스를 이용해서 각 노드별로 숫자를 떨어뜨리는 횟수를 구할 수 있었습니다.
이 횟수를 이용해 이 노드에 숫자를 어떤 순서로 떨어뜨려야 하는지를 구해 봅시다.
사전 순으로 가장 앞선 숫자들을 구해야 하므로, 3을 최대한 많이 사용하고, 그 다음으로 2를 최대한 사용해야 합니다.
그렇게 함으로써 1을 사용하는 빈도가 늘어나고, 사전순으로 앞서게 됩니다.
예를 들어, 숫자 4개를 이용하여 9을 구성해야 하는 경우를 생각해 봅시다.
2-2-2-3, 1-2-3-3 등 여러 조합이 나올 수 있습니다.
하지만 이 중 가장 사전 순으로 앞선 것은 3을 가장 많이 사용한 1-2-3-3입니다.
이 로직을 구현해 봅시다.
숫자를 떨어뜨릴 때에는 최소 1씩은 떨어뜨려야 합니다.
따라서 1은 각 떨어뜨리는 시도 당 미리 깔아 두고, 나머지 숫자를 분배합니다.
예를 들어, 위와 같이 4번의 시도로 9를 만든다면, 4번 각각의 시도에 미리 다음과 같이 1을 깔아 둡니다.
:: 1-1-1-1 ::
이제 남은 숫자인 5를 분배하면 됩니다.
이미 1을 모두 깔아 두었기 때문에 3을 최대한 많이 사용하기 위해서는 남은 숫자를 2로 나누어 그 몫을 계산합니다.
2를 최대한 많이 분배하여 3을 만들어야 하기 때문입니다. 같은 이유로, 2로 나눈 나머지는 2를 사용하는 횟수가 됩니다.
숫자를 떨어뜨리는 시도 당 1씩 깔아 두고, 나머지 숫자 remainder 구하기
remainder를 2로 나눈 몫이 숫자 3을 떨어뜨리는 횟수
remainder를 2로 나눈 나머지가 숫자 2를 떨어뜨리는 횟수
남은 시도들은 모두 숫자 1을 떨어뜨리는 횟수
여기에 해당하는 코드
int[] count = new int[3];
int remainders = value - tries;
count[2] = remainders / 2; // 숫자 3을 떨어뜨리는 횟수
count[1] = remainders % 2; // 숫자 2를 떨어뜨리는 횟수
count[0] = tries - count[1] - count[2]; // 숫자 1을 떨어뜨리는 횟수
이제 이 숫자들을 나열해 주어야 합니다.
배열로 만들 수도 있고, 리스트로 만들 수도 있을 텐데, 결정을 내리기 위해 이것들이 나중에 어떻게 사용될지를 생각해 봅시다.
각 리프 노드 별로 Target 클래스를 만들었고, 리프 노드를 방문하는 순서도 알고 있습니다.
또, 리프 노드 별로 사용되어야 하는 숫자들의 순서도 알고 있죠.
리프 노드를 방문하는 순서를 따라가면서, 사용되어야 하는 숫자들을 하나씩 사용하면 됩니다.
즉, 선입선출을 갖는 자료 구조인 큐를 사용하는 것이 적합해 보입니다.
위에서 구현한 로직을 이용해 큐를 구성하여 반환하는 solve() 메서드를 작성해 줍니다.
Queue<Integer> solve() {
int[] count = new int[3];
int remainders = value - tries;
count[2] = remainders / 2;
count[1] = remainders % 2;
count[0] = tries - count[1] - count[2];
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < count.length; i++) {
for (int j = 0; j < count[i]; j++) {
q.add(i + 1);
}
}
return q;
}
solution 메서드
마지막으로 이 모든 단계를 조합하여 문제를 해결해 줍니다.
private static boolean checkAll(Target[] targets, Function<Target, Boolean> map) {
for (Target t : targets) {
if (t.value == 0) continue;
if (!map.apply(t)) {
return false;
}
}
return true;
}
public int[] solution(int[][] edges, int[] target) {
Node tree = constructTree(edges);
List<Integer> leaves = new ArrayList<>();
Target[] targets = Arrays.stream(target).mapToObj(Target::new).toArray(Target[]::new);
do {
int leaf = tree.trigger().index;
leaves.add(leaf);
targets[leaf].addTry();
if (checkAll(targets, Target::didTooManyTries)) {
return new int[] {-1};
}
} while (!checkAll(targets, Target::isSolved));
List<Queue<Integer>> queues = Arrays.stream(targets).map(Target::solve).collect(Collectors.toList());
return leaves.stream().mapToInt(leaf -> queues.get(leaf).poll()).toArray();
전체 코드
import java.util.*;
import java.util.function.Function;
import java.util.stream.Collectors;
public class Solution {
private static class Node {
public final int index;
private final List<Node> children = new ArrayList<>();
private int childIndex = 0;
Node(int index) {
this.index = index;
}
Node trigger() {
if (isLeaf()) {
return this;
}
Node leaf = children.get(childIndex).trigger();
childIndex = (childIndex + 1) % children.size();
return leaf;
}
void addChild(Node child) {
children.add(child);
}
void sortChild() {
children.sort(Comparator.comparingInt(n -> n.index));
}
private boolean isLeaf() {
return children.isEmpty();
}
}
private static class Target {
public final int value;
private int tries = 0;
Target(int value) {
this.value = value;
}
void addTry() {
tries += 1;
}
boolean isNotEnough() {
return value > tries * 3;
}
boolean didTooManyTries() {
return value < tries;
}
boolean isSolved() {
return !isNotEnough() && !didTooManyTries();
}
Queue<Integer> solve() {
int[] count = new int[3];
int remainders = value - tries;
count[2] = remainders / 2;
count[1] = remainders % 2;
count[0] = tries - count[1] - count[2];
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < count.length; i++) {
for (int j = 0; j < count[i]; j++) {
q.add(i + 1);
}
}
return q;
}
}
private static Node constructTree(int[][] edges) {
Node[] nodes = new Node[edges.length + 1];
for (int i = 0; i < nodes.length; i++) {
nodes[i] = new Node(i);
}
for (int[] edge : edges) {
nodes[edge[0] - 1].addChild(nodes[edge[1] - 1]);
}
for (Node node : nodes) {
if (node == null) continue;
node.sortChild();
}
return nodes[0];
}
private static boolean checkAll(Target[] targets, Function<Target, Boolean> map) {
for (Target t : targets) {
if (t.value == 0) continue;
if (!map.apply(t)) {
return false;
}
}
return true;
}
public int[] solution(int[][] edges, int[] target) {
Node tree = constructTree(edges);
List<Integer> leaves = new ArrayList<>();
Target[] targets = Arrays.stream(target).mapToObj(Target::new).toArray(Target[]::new);
do {
int leaf = tree.trigger().index;
leaves.add(leaf);
targets[leaf].addTry();
if (checkAll(targets, Target::didTooManyTries)) {
return new int[] {-1};
}
} while (!checkAll(targets, Target::isSolved));
List<Queue<Integer>> queues = Arrays.stream(targets).map(Target::solve).collect(Collectors.toList());
return leaves.stream().mapToInt(leaf -> queues.get(leaf).poll()).toArray();
}
}
02024. 06. 17.

프로그래머스 > Java로 코테풀기
경사로의 개수 - Lv. 4 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/214290
2023년 현대 모비스 알고리즘 경진대회 예선 문제라고 한다.
현대 모비스에서 소프트웨어를 강조하기 위해 주최하는 경진대회라고 하는데 어마어마한 상품으로 상당히 화제였었다.
1위 상이 무려 아이오닉 5... 차 한대가 상품이었다.
2등상은 1,000만원 3등상은 500만원으로 역대급 대회였다.
하지만 그런 만큼 진짜 쟁쟁하신 분들이 나오셨다고...
2024년 현대 모비스 알고리즘 경진대회도 총 상금 1억 7천만원이 걸려 있고, 프로그래머스에서 6월 25일까지 접수받고 있다.
=> 2024년 현대 모비스 알고리즘 경진대회 접수
어쨌든 이 문제는 프로그래머스에서 Lv4로 등재되었고, 2차원 배열과 이동 가능한 조건이 주어졌을 때, 이동 가능한 경로의 개수를 찾는 문제이다.
문제 풀기
제한 사항으로 접근법 떠올려보기
문제에서 주어진 제한 사항은 다음과 같습니다.
3 ≤ grid의 길이 = n ≤ 8
3 ≤ grid[i]의 길이 = m ≤ 8
0 ≤ grid[i][j] ≤ 1,000
1 ≤ d의 길이 ≤ 100
1 ≤ k ≤ 10^9
그리드의 크기는 작은 반면, k의 크기는 10억으로 매우 크다는 것을 알 수 있습니다.
k는 d를 반복해야 하는 횟수이므로 k번에 해당하는 만큼 반복을 해야 할 것 같기는 한데, 그 값을 보니 k번 반복을 해서는 안됩니다.
그렇다면 log의 시간 복잡도를 가지는 분할 정복을 떠올릴 수 있습니다.
k를 반으로 나눠가며 연산하는 분할 정복이라면 O(logK)번 만에 k번에 해당하는 반복을 계산해낼 수 있을 것입니다.
이제 문제를 분할 정복에 맞도록 정의할 수 있는지를 확인하면 됩니다.
부분 문제 정의하기
주어진 문제를 분할 정복을 활용해 k번 반복되는 부분 문제로 만들어야 합니다.
문제에서 k번 반복되는 것은 d를 적용하는 횟수입니다.
따라서 d를 적용하는 횟수의 가장 최소 횟수인 1인 문제를 먼저 풀고, 이를 k번 반복하는 것으로 접근할 수 있습니다.
(x1, y1, x2, y2): (x1, y1)에서 (x2, y2)로 d를 이용하여 이동하는 경로의 수
(x1, y1, x2, y2)는 제 책 [취업과 이직을 위한 프로그래머스 코딩 테스트 문제 풀이 전략: 자바편]에서 소개한 문제를 나타내기 위한 표기법으로, 문제를 정의하기 위해 필요한 변수의 집합이라고 생각하시면 됩니다.
더 작은 부분 문제
그런데 위의 문제를 풀기 위해서는 경로를 파악해야 합니다.
이는 다시 부분 문제를 정의하여 다음과 같이 재귀적으로 해결할 수 있습니다.
(x1, y1, x2, y2, di): (x1, y1)에서 (x2, y2)로 d[di]~d[끝]을 이용해서 갈 수 있는 경우의 수 \
= (x1, y1, x, y, i) * (x, y, x2, y2, d.length - i) => 모든 x, y와 di <= i <= d.length에 대한 반복 합
(x1, y1, x2, y2, di)를 풀면, (x1, y1, x2, y2) = (x1, y1, x2, y2, 0)으로 구할 수 있게 됩니다.
이 부분에 해당하는 코드
private static final int DIV = 1_000_000_007;
private static final int[] dx = {1, 0, -1, 0};
private static final int[] dy = {0, 1, 0, -1};
private static int count(
int x1, int y1, int x2, int y2, int di, int[][] grid, int[] d, int[][][][][] mem) {
// Memoization
if (mem[di][x1][y1][x2][y2] != -1) {
return mem[di][x1][y1][x2][y2];
}
// 종료 조건
if (di == d.length) {
if (x1 == x2 && y1 == y2) {
return mem[di][x1][y1][x2][y2] = 1;
} else {
return mem[di][x1][y1][x2][y2] = 0;
}
}
// 재귀
int sum = 0;
for (int i = 0; i < 4; i++) {
int nx = x1 + dx[i];
int ny = y1 + dy[i];
try {
if (grid[ny][nx] == grid[y1][x1] + d[di]) {
sum += count(nx, ny, x2, y2, di + 1, grid, d, mem);
sum %= DIV;
}
} catch (IndexOutOfBoundsException ignored) {
}
}
return sum;
}
private static int[][][][] buildCountMatrix(int[][] grid, int[] d) {
int w = grid[0].length;
int h = grid.length;
// [i][x1][y1][x2][y2]: (x1, y1) -> (x2, y2)를 d[i] ~ d[끝]을 이용해 갈 수 있는 경우의 수
int[][][][][] mem = new int[d.length + 1][w][h][w][h];
for (int di = d.length; di >= 0; di--) {
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
Arrays.fill(mem[di][x1][y1][x2], -1);
for (int y2 = 0; y2 < h; y2++) {
mem[di][x1][y1][x2][y2] = count(x1, y1, x2, y2, di, grid, d, mem);
}
}
}
}
}
return mem[0];
}
부분 문제 시간 복잡도
(x1, y1, x2, y2, di)의 경우 재귀가 진행됨에 따라 반복되는 부분 문제이기 때문에 한 단계의 상태를 구하기 위한 시간 복잡도와 상태의 개수를 이용해 시간 복잡도를 계산할 수 있습니다.
하나의 상태를 구하기 위해서는 d의 길이만큼 반복하고, x, y에 대해서도 반복합니다.
1 <= d의 길이 <= 100
3 <= x, y, <= m = 8
주어진 조건이 위와 같으므로시간 복잡도는 **O(dm²)**이 되고, 최댓값을 대입했을 때 6,400이므로 이 부분 문제는 충분한 시간 복잡도를 가지고 있음을 알 수 있습니다.
분할 정복
(x1, y1, x2, y2)를 해결할 수 있으니, 이를 이용해 k번 반복하는 문제를 해결해야 합니다.
이 문제는 다음과 같이 정의할 수 있습니다.
(x1, y1, x2, y2, r): (x1, y1)에서 (x2, y2)로 d를 r번 이용하여 이동하는 경우의 수
= (x1, y1, x, y, r / 2) * (x, y, x2, y2, r / 2) => r이 짝수일 경우
= (x1, y1, x, y, r / 2) * (x, y, x2, y2, r / 2) * (x1, y1, x2, y2, 1) => r이 홀수일 경우
(x1, y1, x2, y2, 1) = (x1, y1, x2, y2)
모든 x1, y1, x2, y2에 대해 이를 반복한다면 답을 구할 수 있습니다.
그런데 문제가 있습니다. 이 부분 문제는 메모이제이션을 적용할 수 없다는 것입니다.
r의 크기는 최대 10억으로, 이는 메모이즈하기에는 너무 큰 값입니다.
모든 출발점과 도착점에 대해서 같은 연산을 해야 한다는 점을 생각하면 비슷하지만 조금 다른 접근 방식을 생각할 수 있습니다.
행렬 연산
한 점에서 다른 점으로 이동하는 경로의 수는 행렬로 표현할 수 있습니다.
사실, 이미 행렬로 표현되어 있습니다.
문제 (x1, y1, x2, y2)가 풀어낸 답이 바로 그 행렬입니다.
이 문제의 결과는 [x1, y1, x2, y2]의 4차원 배열이 됩니다.
이 배열의 각 원소는 (x1, y1)에서 (x2, y2)로 이동할 수 있는 경로의 수를 가지고 있습니다.
지금 우리가 구해야 하는 것은 (x1, y1)에서 출발하고, (x2, y2)에 도착하지만, 그 과정 중에 어떠한 좌표 (x, y)를 경유하면서 이동하는 경우의 수입니다.
이는 행렬의 곱셈과 같습니다. 즉, 행렬을 k번 거듭제곱하는 것으로 모든 좌표에 대해 같은 연산을 적용할 수 있게 됩니다.
이 부분에 해당하는 코드
private int[][][][] multiply(int[][][][] a, int[][][][] b) {
int w = a.length;
int h = a[0].length;
int[][][][] m = new int[w][h][w][h];
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
for (int y2 = 0; y2 < h; y2++) {
for (int x = 0; x < w; x++) {
for (int y = 0; y < h; y++) {
m[x1][y1][x2][y2] += (int) (((long) a[x1][y1][x][y] * b[x][y][x2][y2]) % DIV);
m[x1][y1][x2][y2] %= DIV;
}
}
}
}
}
}
return m;
}
private int[][][][] power(int[][][][] matrix, int power) {
if (power == 1) {
return matrix;
}
if (power == 2) {
return multiply(matrix, matrix);
}
int[][][][] result = power(power(matrix, power / 2), 2);
if (power % 2 == 1) {
result = multiply(result, matrix);
}
return result;
}
행렬 연산 시간 복잡도
한 번의 재귀 단계에 x1, y1, x2, y2, x, y에 대해서 반복합니다.
반복의 깊이는 log k이므로 전체 시간 복잡도는 **O(log k * m^6)**이 됩니다.
마무리
이제 결과 행렬에서 모든 원소를 순회하며 경로의 개수 합을 구해주면 됩니다.
이 부분에 해당하는 코드
public int solution(int[][] grid, int[] d, int k) {
int[][][][] matrix = buildCountMatrix(grid, d);
matrix = power(matrix, k);
int count = 0;
int w = matrix.length;
int h = matrix[0].length;
//noinspection ForLoopReplaceableByForEach Suppress for better readability.
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
for (int y2 = 0; y2 < h; y2++) {
count += matrix[x1][y1][x2][y2] % DIV;
count %= DIV;
}
}
}
}
return count;
}
전체 시간 복잡도
전체 풀이는 다음의 단계를 따라갑니다.
(x1, y1, x2, y2, di)를 해결하는 부분시간 복잡도: O(dm²)
행렬의 거듭제곱을 계산하는 부분시간 복잡도: O(log k * m^6)
경로 합을 구하는 부분시간 복잡도: O(m⁴)
따라서 전체 시간 복잡도는 O(dm²) + O(log k * m^6) + O(m⁴) = O((d + log k * m⁴)m²)이 되고,
최댓값을 고려했을 때 d < log k * m⁴d이므로 **O(log k * m^6)**이 됩니다.
제한 사항을 고려해 최댓값을 대입하면 약 784만이라는 값이 나와, 충분한 시간 복잡도라는 것을 알 수 있습니다.
전체 코드
import java.util.Arrays;
public class Solution {
private static final int DIV = 1_000_000_007;
private static final int[] dx = {1, 0, -1, 0};
private static final int[] dy = {0, 1, 0, -1};
private static int count(
int x1, int y1, int x2, int y2, int di, int[][] grid, int[] d, int[][][][][] mem) {
// Memoization
if (mem[di][x1][y1][x2][y2] != -1) {
return mem[di][x1][y1][x2][y2];
}
// 종료 조건
if (di == d.length) {
if (x1 == x2 && y1 == y2) {
return mem[di][x1][y1][x2][y2] = 1;
} else {
return mem[di][x1][y1][x2][y2] = 0;
}
}
// 재귀
int sum = 0;
for (int i = 0; i < 4; i++) {
int nx = x1 + dx[i];
int ny = y1 + dy[i];
try {
if (grid[ny][nx] == grid[y1][x1] + d[di]) {
sum += count(nx, ny, x2, y2, di + 1, grid, d, mem);
sum %= DIV;
}
} catch (IndexOutOfBoundsException ignored) {
}
}
return sum;
}
private static int[][][][] buildCountMatrix(int[][] grid, int[] d) {
int w = grid[0].length;
int h = grid.length;
// [i][x1][y1][x2][y2]: (x1, y1) -> (x2, y2)를 d[i] ~ d[끝]을 이용해 갈 수 있는 경우의 수
int[][][][][] mem = new int[d.length + 1][w][h][w][h];
for (int di = d.length; di >= 0; di--) {
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
Arrays.fill(mem[di][x1][y1][x2], -1);
for (int y2 = 0; y2 < h; y2++) {
mem[di][x1][y1][x2][y2] = count(x1, y1, x2, y2, di, grid, d, mem);
}
}
}
}
}
return mem[0];
}
private int[][][][] multiply(int[][][][] a, int[][][][] b) {
int w = a.length;
int h = a[0].length;
int[][][][] m = new int[w][h][w][h];
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
for (int y2 = 0; y2 < h; y2++) {
for (int x = 0; x < w; x++) {
for (int y = 0; y < h; y++) {
m[x1][y1][x2][y2] += (int) (((long) a[x1][y1][x][y] * b[x][y][x2][y2]) % DIV);
m[x1][y1][x2][y2] %= DIV;
}
}
}
}
}
}
return m;
}
private int[][][][] power(int[][][][] matrix, int power) {
if (power == 1) {
return matrix;
}
if (power == 2) {
return multiply(matrix, matrix);
}
int[][][][] result = power(power(matrix, power / 2), 2);
if (power % 2 == 1) {
result = multiply(result, matrix);
}
return result;
}
public int solution(int[][] grid, int[] d, int k) {
int[][][][] matrix = buildCountMatrix(grid, d);
matrix = power(matrix, k);
int count = 0;
int w = matrix.length;
int h = matrix[0].length;
//noinspection ForLoopReplaceableByForEach Suppress for better readability.
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
for (int y2 = 0; y2 < h; y2++) {
count += matrix[x1][y1][x2][y2] % DIV;
count %= DIV;
}
}
}
}
return count;
}
}
02024. 06. 17.

프로그래머스 > Java로 코테풀기
아날로그 시계 - Lv 2 문제 풀이 (실수 비교 안하기)
https://school.programmers.co.kr/learn/courses/30/lessons/250135
주어진 시간 범위 내에서 초침이 분침 / 시침과 겹치는 횟수를 세는 문제이다.
문제 이해하기
다음과 같은 조건들로 인해 제약 사항이 생긴다.
각 바늘은 연속적으로 움직인다.바늘이 겹치는 시간이나 각도가 실수이기 때문에 정확한 비교는 힘들다.
1초 안에 초침이 다른 하나의 바늘과 두 번 겹치는 경우는 없다.초침-분침, 초침-분침 과 같이 분침과 두 번 겹칠 일은 없다.
다만, 초침-분침, 초침-시침과 같이 서로 다른 두 바늘과 겹칠 수는 있다.
간단히 생각하면, 그냥 1초씩 시간을 흘려가면서 각 바늘의 각도를 계산해가면서 초침이 분침이나 시침의 각도를 넘어서는 횟수를 세주면 될 것이다. 딱 여기까지라면 정말 Lv2인 이 문제에 알맞는 난이도라고 생각했을 것이다.
하지만 문제는 시침과 분침, 초침이 한 번에 겹치게 되면 한 번으로 세주어야 하는 데에서 발생했다. 위 접근법은 1초 내에 초침이 분침 또는 시침과 겹친 적이 있는지를 판별할 수는 있지만, 셋 모두가 동시에 겹쳤다는 것을 판단할 수는 없다. 분침-시침이 겹치는 것을 별도로 판별했다고 하더라도, 이 시점이 초침과 겹쳐지는 시점과 달라질 수 있기 때문에 정확하지 않다.
세 바늘이 동시에 겹쳤는지를 판단하기 위해서는 1초 내에서도 언제 겹쳤는지 정확한 시간을 계산하여 비교하던가, 바늘이 겹쳤을 때의 정확한 각도를 계산하여 비교할 수 있어야 한다.
나이브한 접근 - 실수 비교
이게 Lv 2라고? 하는 생각이 들어 다른 사람들의 풀이를 찾아보았다. 놀랍게도 대다수의 사람들이 무려 실수 비교를 통해 바늘이 겹치는 것을 검사하고 있었다. 세 바늘의 각도를 double로 표현하고, 이 각도가 서로 일치하는지를 검사한 것이다.
조금 세게 말하자면, 정말 말도 안되는 풀이라고 생각했다.
프로그래밍을 처음 공부할 때 배우는 것이 실수형의 한계이다. 컴퓨터는 0과 1로 한정된 비트 수를 사용하여 실수를 표현하기 때문에 실수를 정확하게 표현할 수 없고, 오차가 발생한다는 것은 누구나 알고 있다.
따라서 실수형을 다룰 때에는 정확한 값을 가지고 있을 것이라는 생각 자체를 하면 안된다. 다시 말해, 실수형에 == 연산은 해당 값에 부동 소수점 오차가 없다는 완벽한 근거 없이는 절대 해서는 안되는 연산이라는 것이다. 이로 인해 실수형은 대부분 비교 연산을 수행하거나, 일정 수준의 threshold를 두고, 해당 오차 범위 안의 값인지를 검사한다.
그런데 정확성이 중요한 코딩 테스트에서 실수형 비교를 통해 문제를 해결한다니, 말이 안된다고 생각했다.
이러한 방법을 사용한 풀이가 통과된 것은, 단순히 시침, 분침, 초침이 겹치는 시간이 12시 00분 00초 밖에 없기 때문이다. 이 때는 각도가 0이므로 소수점 오차가 발생하지 않는다. 만약 다른 각도에서 세 바늘이 겹치는 현상이 발생했다면, 이 코드들은 통과하지 못했을 것이다.
또, 정확히 12시에만 세 바늘이 겹친다는 것을 알고 있었다면 실수형 비교를 할 이유가 없다. 그저 시간이 12시 정각인지를 검사하는 것을 통해 훨씬 간단하게 체크할 수 있기 때문이다. 다시 말해, 각도를 실수로 표현하고, 이를 동등 비교하는 것은 이 문제 풀이에서 나와서는 안되는, 운으로 통과하는 케이스라고 생각한다.
구현으로 풀기
세 바늘의 각도를 비교해야 한다는 것에는 이견이 없다. 다만, 이를 실수형으로 나타내고 푸는 것이 위험하다는 것이다. 다행히도, 빡센 구현을 통해 부동 소수점 오차 걱정 없이 문제를 해결할 수 있다.
Fraction 클래스
이를 해결하기 위해서는 각도를 분수로 나타내면 된다. 앞선 포스트 자바로 분수 나타내기에서 다룬 Fraction 클래스를 이용하면 각도를 온전히 나타낼 수 있다. 몇몇 메서드가 이 문제에 맞춰 수정되었지만, 큰 뼈대는 같으니 설명 없이 코드만 첨부한다.
private static class Fraction implements Comparable<Fraction> {
public final long numerator;
public final long denominator;
public Fraction(int value) {
this(value, 1);
}
public Fraction(long numerator, long denominator) {
long gcd = gcd(Math.abs(numerator), Math.abs(denominator));
this.numerator = numerator / gcd;
this.denominator = denominator / gcd;
}
public Fraction add(int value) {
return new Fraction(numerator + value * denominator, denominator);
}
public Fraction add(Fraction other) {
long numerator = this.numerator * other.denominator + this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction subtract(Fraction other) {
long numerator = this.numerator * other.denominator - this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction multiply(Fraction other) {
long numerator = this.numerator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction divide(Fraction other) {
return multiply(other.inverse());
}
public Fraction inverse() {
if (numerator == 0) {
throw new ArithmeticException("Cannot inverse zero.");
}
return new Fraction(denominator, numerator);
}
public Fraction mod(int value) {
return new Fraction(numerator % (value * denominator), denominator);
}
public double value() {
return (double) numerator / denominator;
}
@Override
public boolean equals(Object object) {
if (this == object) return true;
if (object == null || getClass() != object.getClass()) return false;
Fraction other = (Fraction) object;
return numerator == other.numerator && denominator == other.denominator;
}
@Override
public int compareTo(Fraction f) {
if (equals(f)) {
return 0;
} else if (value() < f.value()) {
return -1;
} else {
return 1;
}
}
private static long gcd(long a, long b) {
if (b == 0) return a;
return gcd(b, a % b);
}
}
Clock 클래스
시계를 나타내는 Clock 클래스이다. 세 바늘의 각도와 현재 시간, 초침이 다른 바늘과 겹치는 연산을 수행해줄 클래스가 될 것이다.
먼저, 각 바늘이 초 당 몇 도나 회전하는지를 Fraction으로 나타내어준다.
시침은 360도를 12(시간)* 60(분) * 60(초) 만에 돈다.
분침은 360도를 60(분) * 60(초) 만에 돈다.
초침은 360도를 60(초) 만에 돈다.
private static class Clock {
private static final Fraction HOUR_APS = new Fraction(360, 12 * 60 * 60);
private static final Fraction MINUTE_APS = new Fraction(360, 60 * 60);
private static final Fraction SECOND_APS = new Fraction(360, 60);
}
다음으로, 현재 시간과 각 바늘의 각도를 Fraction으로 나타내어준다.
private Fraction time;
private Fraction hourAngle;
private Fraction minuteAngle;
private Fraction secondAngle;
생성자에서는 현재 시간을 입력 받고, 이에 맞게 각 바늘의 각도를 계산해준다.
여기서 중요하게 생각해야 할 점이 바로 초침이 시침이나 분침보다 빠르다는 점이다.
이는 초침이 각도 상 뒤에 있어야 (즉, 더 작은 각도를 가지고 있어야) 분침과 시침을 따라잡는 연산이 쉬워진다는 의미이다.
따라서, 분침이나 시침이 초침보다 더 작은 각도를 가지고 있다면, 한 바퀴를 추가로 회전시켜 (360을 더하여) 더 큰 각도를 가지고 있게 만들어준다.
public Clock(int time) {
this.time = new Fraction(time);
alignAngles();
}
private void alignAngles() {
hourAngle = HOUR_APS.multiply(time).mod(360);
minuteAngle = MINUTE_APS.multiply(time).mod(360);
secondAngle = SECOND_APS.multiply(time).mod(360);
if (minuteAngle.compareTo(secondAngle) <= 0) {
minuteAngle = minuteAngle.add(360);
}
if (hourAngle.compareTo(secondAngle) <= 0) {
hourAngle = hourAngle.add(360);
}
}
다음으로 구현할 메서드는 알람이 울리는 다음 시간으로 이동하고, 해당 시간을 반환하는 nextRing() 메서드이다.
public Fraction nextRing() {
...
}
초침이 분침과 시침을 따라 잡는 시간을 계산하기 위해서는, 각 바늘 사이의 각도와 초 당 얼마만큼의 각도를 초침이 따라잡는지를 알아야 한다.
초침이 분침과 시침을 따라잡는 속도는 각 바늘이 가지는 속도의 차이이므로 다음과 같이 나타낼 수 있다.
private static final Fraction HOUR_FOLLOW_APS = SECOND_APS.subtract(HOUR_APS);
private static final Fraction MINUTE_FOLLOW_APS = SECOND_APS.subtract(MINUTE_APS);
이를 이용하면, 초침이 분침과 시침을 따라잡는 시간은 다음과 같이 계산된다.
Fraction timeToNextHour = hourAngle.subtract(secondAngle).divide(HOUR_FOLLOW_APS);
Fraction timeToNextMinute = minuteAngle.subtract(secondAngle).divide(MINUTE_FOLLOW_APS);
이 두 시간 중 더 빠른 시간에 먼저 종이 울릴 것이므로, 다음과 같이 시간을 업데이트 해준다.
switch (timeToNextHour.compareTo(timeToNextMinute)) {
case -1: // 초침-시침 충돌
case 0: // 초침-시침-분침 충돌
time = time.add(timeToNextHour);
break;
case 1: // 초침-분침 충돌
time = time.add(timeToNextMinute);
break;
}
마지막으로 업데이트된 시간으로 바늘의 각도를 재조정하고, 시간을 반환해준다.
alignAngles();
return time;
nextRing() 메서드는 현재 시간에서 알람이 울리는지는 검사하지 않는다. 따라서 가장 처음 Clock 객체를 생성했을 때 알람이 울리는 시간인지를 판별해 줄 doesRing() 메서드도 하나 넣어준다.
public boolean doesRing() {
return secondAngle.equals(hourAngle.mod(360)) || secondAngle.equals(minuteAngle.mod(360));
}
각도를 실수형이 아니라 정수형을 갖는 분수로 표현했기 때문에 equals() 메서드를 사용해서 정확히 비교할 수 있다.
solution() 메서드
Clock 클래스가 준비되었으면 횟수를 세는 것은 쉽다.
입력받은 시간으로 Clock 객체를 초기화하고, 시간 범위 밖으로 나갈 때 까지 nextRing()을 호출하며, 그 횟수를 세주면 된다.
public int solution(int h1, int m1, int s1, int h2, int m2, int s2) {
int from = h1 * 60 * 60 + m1 * 60 + s1;
int to = h2 * 60 * 60 + m2 * 60 + s2;
Clock clock = new Clock(from);
int count = 0;
if (clock.doesRing()) {
count = 1;
}
while (true) {
double time = clock.nextRing().value();
if (time > to) return count;
count += 1;
}
}
마무리
분수와 시계의 구현을 통해 프로그래머스 PCCP 기출문제 아날로그 시계를 풀어 보았다.
구현할 양이 많기는 해서 Lv 2는 아닌 것 같긴 하다.
내 생각이지만, Lv 2라고 매겨놓은 근거는 구현으로 푸는 것이 아니라 실제로 바늘이 언제 겹치는지는 손으로 미리 계산을 하고, 주어진 시간 범위 내에 겹치는 사건이 얼마나 발생하는지를 판별하라는 것 같다.
그런데 이 방법도 마찬가지로 초침과 분침, 초침과 시침이 얼마나 겹치는지는 계산할 수 있을 것 같은데, 초침-분침-시침이 모두 한 번에 겹치는 것이 12시 정각밖에 없다는 것을 어떻게 증명하는지를 사실 잘 모르겠다.
전체 코드
public class Solution {
private static class Fraction implements Comparable<Fraction> {
public final long numerator;
public final long denominator;
public Fraction(int value) {
this(value, 1);
}
public Fraction(long numerator, long denominator) {
long gcd = gcd(Math.abs(numerator), Math.abs(denominator));
this.numerator = numerator / gcd;
this.denominator = denominator / gcd;
}
public Fraction add(int value) {
return new Fraction(numerator + value * denominator, denominator);
}
public Fraction add(Fraction other) {
long numerator = this.numerator * other.denominator + this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction subtract(Fraction other) {
long numerator = this.numerator * other.denominator - this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction multiply(Fraction other) {
long numerator = this.numerator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction divide(Fraction other) {
return multiply(other.inverse());
}
public Fraction inverse() {
if (numerator == 0) {
throw new ArithmeticException("Cannot inverse zero.");
}
return new Fraction(denominator, numerator);
}
public Fraction mod(int value) {
return new Fraction(numerator % (value * denominator), denominator);
}
public double value() {
return (double) numerator / denominator;
}
@Override
public boolean equals(Object object) {
if (this == object) return true;
if (object == null || getClass() != object.getClass()) return false;
Fraction other = (Fraction) object;
return numerator == other.numerator && denominator == other.denominator;
}
@Override
public int compareTo(Fraction f) {
if (equals(f)) {
return 0;
} else if (value() < f.value()) {
return -1;
} else {
return 1;
}
}
private static long gcd(long a, long b) {
if (b == 0) return a;
return gcd(b, a % b);
}
}
private static class Clock {
private static final Fraction HOUR_APS = new Fraction(360, 12 * 60 * 60);
private static final Fraction MINUTE_APS = new Fraction(360, 60 * 60);
private static final Fraction SECOND_APS = new Fraction(360, 60);
private static final Fraction HOUR_FOLLOW_APS = SECOND_APS.subtract(HOUR_APS);
private static final Fraction MINUTE_FOLLOW_APS = SECOND_APS.subtract(MINUTE_APS);
private Fraction time;
private Fraction hourAngle;
private Fraction minuteAngle;
private Fraction secondAngle;
public Clock(int time) {
this.time = new Fraction(time);
alignAngles();
}
public boolean doesRing() {
return secondAngle.equals(hourAngle.mod(360)) || secondAngle.equals(minuteAngle.mod(360));
}
public Fraction nextRing() {
Fraction timeToNextHour = hourAngle.subtract(secondAngle).divide(HOUR_FOLLOW_APS);
Fraction timeToNextMinute = minuteAngle.subtract(secondAngle).divide(MINUTE_FOLLOW_APS);
switch (timeToNextHour.compareTo(timeToNextMinute)) {
case -1: // 초침-시침 충돌
case 0: // 초침-시침-분침 충돌
time = time.add(timeToNextHour);
break;
case 1: // 초침-분침 충돌
time = time.add(timeToNextMinute);
break;
}
alignAngles();
return time;
}
private void alignAngles() {
hourAngle = HOUR_APS.multiply(time).mod(360);
minuteAngle = MINUTE_APS.multiply(time).mod(360);
secondAngle = SECOND_APS.multiply(time).mod(360);
if (minuteAngle.compareTo(secondAngle) <= 0) {
minuteAngle = minuteAngle.add(360);
}
if (hourAngle.compareTo(secondAngle) <= 0) {
hourAngle = hourAngle.add(360);
}
}
}
public int solution(int h1, int m1, int s1, int h2, int m2, int s2) {
int from = h1 * 60 * 60 + m1 * 60 + s1;
int to = h2 * 60 * 60 + m2 * 60 + s2;
Clock clock = new Clock(from);
int count = 0;
if (clock.doesRing()) {
count = 1;
}
while (true) {
double time = clock.nextRing().value();
if (time > to) return count;
count += 1;
}
}
}
02024. 06. 09.
