43개 게시글
일상
실내 창틀에서 키운 다이소 상추 깻잎 첫 재배! (씨앗부터 키운 과정)
다이소에서 씨앗을 사서 심은지 어느덧 한 달 반.
처음부터 튼튼했던 깻잎은 물론, 상추도 꽤 자랐다.
이중창이라 방충망과 안쪽 샷시 사이에서 키우고 있는데 생각보다 잘 자라주고 있다.
아직 작지만 밥 먹을 때 쌈용으로 몇 장 뜯어봤다.
주문한 제육과 같이 먹어봤는데, 진짜 상추와 깻잎 맛이 나는 것이 당연하면서도 신기하게 느껴졌다.
6월에 구리로 이사하고 나서 레몬 나무를 키우기 위한 예행 연습으로 시작한 상추 깻잎 키우기가 어느 정도 결실을 맺은 것 같아 감회가 새롭다.
씨앗을 심기부터 지금까지의 과정을 정리해보고자 한다.
페트병 저면관수 (3월 21일)
투명한 페트병과 물티슈를 이용하여 물을 줄 필요가 없는 저면관수 시스템을 만들 수 있다는 유튜브 영상을 봤다.
지금은 브리타 정수기를 쓰지만 당시에는 탐사수를 시켜 먹고 있었기 때문에 페트명은 충분했다.
깻잎과 상추 씨앗을 뿌리고 흙을 살짝 덮은 뒤, 물을 한 번 주고 창가에 자리잡았다.
발아는 그늘에서 하는게 좋다고 하던 것 같은데 씨앗을 꽤 많이 뿌렸기 때문에 몇 개만 걸려라 식으로 그냥 창가에 두었다.
상추 발아 (3월 23일)
상추 씨앗이 이틀만에 먼저 발아했다.
조그맣던 상추가 다음날 되니 더욱 자랐다.
깻잎 발아 (3월 27일)
거의 일주일이 지나서야 깻잎이 발아했다.
너무 소식이 없어 상추만 키워야 하나 했는데 드디어 싹이 났다.
생각보다 싹이 많이 났다.
상추도 싹이 더 자랐고, 새로운 싹이 텄다.
계속 돌려주기
싹이 점점 자라면서 햇빛쪽으로 휘는 것이 보였다.
깻잎 싹은 비교적 키가 작아 크게 느껴지지 않았지만, 상추는 키가 커 너무 잘 보였다.
계속 페트병을 돌려가면서 너무 한 쪽으로 치우지지 않도록 했다.
1차 분갈이 (4월 22일)
상추가 싹도 먼저 나고 키도 더 잘커서 깻잎만 걱정하고 있었는데 시간이 지나면서 그렇지 않다는 것이 드러났다.
건강한 녹색으로 잎을 펼친 깻잎과 달리 상추는 흐물흐물하고 잘 자라지도 못했다.
투명 페트병이라 흙 옆면에 이끼도 끼었다.
식물의 성장에 방해가 되지는 않는다지만 신경 쓰이긴 했다.
과습의 영향일 수도 있을 것 같아 분갈이를 하기로 마음먹었다.
한 달 동안 물을 주거나 따로 신경쓰지 않아도 잘 자라주었지만, 이제는 진짜 화분에 옮겨 직접 물을 주며 키워보기로 했다.
레몬 나무의 예행 연습인걸 생각하면 그 편이 나은 것 같기도 했다.
우선 직접 만들었던 저면관수 페트병에서 식물을 빼주었다.
적상추 4개, 깻잎은 8개가 나왔다.
쿠팡에서 산 화분에 마사토를 깔고, 남아있던 다이소 상토와 기존에 있던 흙을 섞어 넣어주었다.
가지고 있던 흙이 부족하여 새 흙에 기존 흙을 같이 써야 했다.
그 다음 흙에 구멍을 조금씩 파 식물들을 심었다.
분갈이를 하고 나서 보니 흙의 높이가 많이 낮아보였다.
상추 또한 힘이 없는 것이 더욱 확연히 보였다.
상추가 아직 키가 작아 흙이 저렇게 낮으면 빛을 충분히 못 받을 여지가 컸다.
그러나 짧은 시간 안에 흙을 보충하는 분갈이를 한 번 더 하면 스트레스가 너무 클 것 같았다.
결국 일단은 상추가 분갈이에 적응할때까지 기다렸다가, 건강해지면 그 이후에 흙을 보충하는 분갈이를 한 번 더 하기로 했다.
지금은 상추가 너무 스트레스 받지 않게 반양지에 두었다.
2차 분갈이 (4월 30일)
일주일을 기다려 봤는데 상추는 회복할 기미가 보이지 않았다.
거름과 함께 영양소 있는 흙을 보충해주는 2차 분갈이를 해주고 경과를 조금 더 지켜보기로 했다.
새로운 흙은 배양토에 계란 껍질 가루, 린클 미생물 흙을 섞어 일주일동안 놔둔 흙이다.
저번처럼 식물들을 조심스레 분리하고, 새 흙을 기존의 흙과 잘 섞어가며 보충해 준 다음 다시 심어주었다.
상추가 힘이 없어 축 쳐져 있는데, 물을 주니 흙이 상추 위로 덮여 곤란했다.
이번에는 햇빛을 잘 볼수 있게 창가로 옮겨놨다.
확실히 흙의 높이가 높아지니 햇빛을 더욱 잘 받을 것 같다.
상추 소생
시간이 지나면서 상추가 점점 정신을 차리는 것 같았다.
맨눈으로 볼 때는 느낌인지 진짜 살아나는 건지 확실하지 않았는데 사진으로 보니 확실히 조금씩 살아나는 것 같다.
5월 2일에는 바닥에 붙어있던 상추가 조금 힘이 생겨 고개를 들기 시작했다.
5월 7일에는 잎이 넓어지고 힘이 더 생겼다.
5월 9일에는 대부분의 잎에 힘이 붙었다. 만졌을 때도 상추잎의 대가 튼튼하게 느껴졌다.
5월 13일에는 상추 옆에서 확실히 자리를 잡고 잎을 뻗어냈다.
5월 16일에는 노랗던 색도 건강한 녹색으로 바뀌면서 건강을 되찾았다는 신호가 확실히 보였다.
그리고 대망의 5월 17일. 오늘 아침에는 비가 온 뒤 맑게 갠 파란 하늘과 함께 건강하고 큰 잎들을 자랑하고 있었다.
상추도 건강해진 것이 확실하고, 깻잎 또한 점점 자라면서 아래쪽에 있는 잎이 햇빛을 잘 못 받고 있었다.
지금 집의 공간으로서는 화분을 넓히기에는 무리가 있다.
건강하지 않은 잎도 제거해주고 상추의 소생을 기념도 할 겸 아래쪽에 햇빛을 잘 못 받는 잎들을 뜯어서 먹어보았다.
린클과 계란 껍질 가루를 비료로 활용하는 것을 실제로 해보고 효과도 봤으니, 이사가고 나서의 린클 -> 비료 -> 수확 -> 린클 의 사이클이 어느 정도 검증됐다고 생각해도 될까?
02025. 05. 17.
웹
Footer를 페이지 하단에 고정하는 법
대부분의 웹페이지는 Footer가 있으며, 페이지 내용의 길이에 상관 없이 하단에 고정되어 있다.
내용이 짧으면 알아서 페이지의 하단에 붙고, 내용이 길다면 스크롤해야 보이는 Footer를 만들어보자.
페이지 준비
우선 다음과 같이 간단한 페이지 구조를 만들었다.
<body>
<header class="header">Header</header>
<div class="content">
Content
</div>
<footer class="footer">Footer</footer>
</body>
body {
margin: 0;
}
.header {
background-color: yellow;
}
.content {
background-color: green;
}
.footer {
background-color: skyblue;
}
Header, Content, Footer를 색으로 구분하였다.
실제 웹페이지에서는 Content 안에 내용이 들어가게 될 것이다.
내용이 짧아 Footer가 위로 붙어있는 모습을 확인할 수 있다.
조건
Footer가 페이지 하단에 고정되기 위해서는 다음의 조건을 만족해야 한다.
내용이 짧을 때는 Content가 길어져야 한다.단, 페이지를 넘어가게 길어져서는 안된다.
내용이 길 때에는 Content가 내용에 맞는 높이만큼 사용해야 한다.
즉, Content의 높이가 Footer를 하단에 고정하는 데 핵심이라고 할 수 있다.
구현
우선, body가 차지하는 높이 자체를 늘려 주어야 한다.
그래야 Content도 그 안에서 원하는 만큼 길이를 가질 수 있을 것이다.
최소 높이, 즉 min-height를 활용하면 내용이 짧을 때에만 효과를 낼 수 있을 것이다.
body {
margin: 0;
min-height: 100vh;
}
그 다음, Content가 body에서 남는 공간을 전부 차지하도록 해야 한다.
이를 위해 body는 flex로 설정하고, Content에는 flex-grow: 1을 준다.
body {
margin: 0;
min-height: 100vh;
display: flex;
flex-direction: column;
}
.content {
background-color: green;
flex-grow: 1;
}
이렇게만 하면 끝이다.
결과
내용이 짧을 때, Content가 늘어나 Footer가 하단에 고정된 것을 볼 수 있다.
스크롤바 또한 생기지 않는다.
내용이 길어 페이지를 넘어갈 경우, 정상적으로 스크롤바가 생겨 Footer는 페이지 아래로 밀려난다.
스크롤을 아래로 내려보면, Footer가 내용을 가리거나 하는 것 없이 하단에 잘 보여지고 있는 모습도 확인할 수 있다.
<body>
<header class="header">Header</header>
<div class="content">
Content
</div>
<footer class="footer">Footer</footer>
</body>
body {
margin: 0;
min-height: 100vh;
display: flex;
flex-direction: column;
}
.header {
background-color: yellow;
}
.content {
background-color: green;
flex-grow: 1;
}
.footer {
background-color: skyblue;
}
02025. 04. 22.
웹
이미지 hover 시 오버레이 보여주기
<div class="container">
<img class="image" src="https://picsum.photos/200" />
<div class="overlay">
Overlay content here
</div>
</div>
.container {
position: relative;
display: inline-block;
cursor: pointer;
}
.image {
display: block;
}
.overlay {
background-color: #000000ff;
color: white;
opacity: 0;
transition: opacity 120ms;
position: absolute;
top: 0;
left: 0;
right: 0;
bottom: 0;
/* 텍스트 가운데 정렬 */
display: flex;
align-items: center;
justify-content: center;
}
.overlay:hover {
opacity: 0.7;
}
이미지에 커서를 hover 했을 때 overlay content가 보여진다.
이미지의 크기에 따라 container의 사이즈도 변경된다.
이미지와, 이를 감싸는 컨테이너를 먼저 배치하고,
overlay 엘리먼트를 컨테이너 전체 면적을 차지하도록 absolute로 설정한다.
hover 시 opacity를 조정해주면 hover시에만 해당 내용을 보여줄 수 있게 된다.
:: 위 이미지에서 테스트해보자. ::
https://jsfiddle.net/rn3e4c5d/20/
02025. 01. 11.
일상
내가 생각하는 구글 최고의 복지 세 가지
2020년에 대학교를 졸업하고 6월에 구글 코리아에 입사했다.
그로부터 벌써 4년 반이 지났다.
팀도 여러 번 옮기고 프로젝트도 여러 개를 했지만 모든 기간 내가 생각하기에 최고라고 느낀 복지 세 가지가 있다.
이번 포스트에서 그 세 가지 복지를 짚어보고자 한다.
1. 자율 출퇴근
구글은 자율 출퇴근제이다.
출근 시간과 퇴근 시간이 정해져있아 않고 내 일정에 맞춰서 일하면 된다.
하루에 8시간 이상, 일주일에 40시간 이상 등의 최소 근무 시간도 없다.
이러한 자율 출퇴근은 내가 최고의 효율을 낼 수 있도록 많은 도움을 주는 복지라고 생각한다.
코딩 테스트 책 출판 이후 요즘 IT와의 인터뷰에서도 자율 출퇴근에 대해서 이야기 한 적이 있다.
https://yozm.wishket.com/magazine/detail/2460/
자율 출퇴근제를 활용하면 내 라이프 스타일에 맞게끔 업무 시간을 조정할 수 있다.
오후와 저녁에 약속이 많은 사람은 최대한 오전 시간을 활용해서 업무를 하고,
오전에 일정이 많은 사람은 오후와 저녁 시간대에 업무를 할 수 있다.
실제로 나는 한동안 야간이나 오전에 배드민턴을 치고, 점심 시간 끝나갈 때 쯤 출근하는 일과를 꽤 오래 유지했다.
구글에서는 이렇게 점심 때 돼서야 회사에 나오는 것을 존중해주는, 아니, 아예 신경 쓰지 않는 분위기이다.
또, 러시아워를 피함으로써 출퇴근 스트레스를 줄일 수 있다.
역삼에서 서울대입구쪽으로 이사오고 나서 출퇴근 거리가 늘었다.
가장 힘들었던 것은 지하철에 사람이 너무 많았다.
역삼에서 오피스 5분 거리에 살 때만 해도 아침에 일어나서 오피스에 금방 걸어가고, 퇴근하고 싶을 때 퇴근할 수 있었는데 이사오고 나니 출퇴근 할 때 사람이 너무 많아 힘들었다.
이 때문에 출퇴근 시간이 자연스레 늦어졌다.
출근 시간이 지나고 사람이 많이 없을 때 출근하고, 마찬가지로 퇴근 시간이 지나고 퇴근한다.
출퇴근할 때 받는 스트레스가 줄어드니 출퇴근도 할만 했다.
2. 음식
구글, 그 중에서도 구글 코리아는 음식이 맛있기로 유명했다.
구글 코리아 오피스에는 두 개의 식당이 있는데, 각 식당은 다르게 운영된다.
하나는 메인 디시 하나와 뷔페식으로 운영되는 사이드 디시들이 있다.
또 다른 하나는 라이스 메뉴나 누들 메뉴를 메인으로 제공하고, 반찬이 있는 식당이다.
메뉴도 매번 바뀌고, 양도 마음껏 먹을 수 있다.
특히 건강하게 먹으려면 얼마든지 건강하게 먹을 수 있고, 반대로 또 얼마든지 안 건강하게 먹을 수 있다는 점에서 그날그날 기분에 따라 맞춰 먹을 수 있다는 점도 큰 것 같다.
아침과 점심을 제공해주는데, 아침은 김밥이나 국밥처럼 간단하게 먹을 수 있는 메뉴 위주이다.
또, TGIT (Thanks God It's Thursday)가 별도로 운영된다.
이건 구글의 TGIF(Thanks God It's Friday)로 널리 알려져 있는데, 시차 때문에 한국에서는 목요일에 하는 것으로 바뀌었다.
여기서는 특별식처럼 맛있는 메뉴들이 종종 나온다.
맥주나 위스키처럼 술도 나오지만 나는 술을 별로 안좋아해서 잘 마시지는 않는다.
3. 사람
이건 정말 빼놓을 수 없는 복지이다.
구글에서 만나게 된 사람들은 전부 자신의 일에 열정을 가지고 있다.
말로는 매번 귀찮다, 집에 가고 싶다, 이런 거 왜 해야 하냐 하지만 막상 보면 "그래도 대충 할 순 없잖아?" 하면서 엄청난 능력을 보여준다.
단순히 코딩 뿐만 아니라 프로젝트 방향성이나 문제 파악, 해결 등 다방면으로 능력을 가진 사람들이 참 많다.
옆에 있는 이런 사람들을 보면 내가 어떤 역량이 부족한지를 확실히 깨닫게 된다.
구글 코리아에서는 직급에 관계 없이 "님" 호칭을 사용한다.
서로 존중하는 문화가 있기에 혼날 걱정 없이 모르는 것을 마음껏 물어볼 수 있다.
혹시나 가끔 답답해할까 걱정하며 조심스럽게 물어보면, 의자까지 끌고와 성심성의껏 설명해주며 코드 포인터까지 공유해준다.
해외에 있는 팀들과의 교류도 굉장히 많은 도움이 된다.
한국에 있는 팀원들이 모르는 것이 있으면 해외에 있는 팀원들에게 물어보고, 자세한 답변을 얻을 수 있다.
반대로 한국 팀이 더 잘 알고 있는 내용이 있으면 우리가 도움을 주기도 한다.
이렇게 서로 교류하며 다른 오피스에서 진행하는 프로젝트 이야기를 듣다보면 시야도 넓어지고 프로젝트 방향성도 점점 명확해지는 느낌이다.
최고의 복지는 동료다. 라고 했던가.
이러한 동료들이 있기에 나도 더욱 성장할 수 있고 회사도 점점 더 발전할 수 있는 것 같다.
02025. 01. 09.
Flutter
안드로이드 adb 무선 연결 디버깅하기
안드로이드는 adb (Android Debug Bridge)를 통해 디버깅 연결을 할 수 있다.
Flutter 뿐만 아니라 안드로이드 스튜디오로 진행하는 네이티브 안드로이드 개발도 adb를 통한다.
유선 연결하여 프로젝트를 실행하고 디버깅하는 것이 일반적이지만, adb는 무선 디버깅도 지원한다.
나는 휴대폰을 유선 충전하면서 프로젝트를 디버깅하는 경우가 많아 무선 디버깅을 애용한다.
안드로이드 무선 디버깅하기
무선 디버깅을 연결하는 방법을 살펴보기 전, 다음을 확인하자.
데스트탑에 adb가 설치되어 있어야 한다.cmd에 adb를 쳤을 때 adb로 할 수 있는 명령어 리스트가 출력돼야 한다.
안드로이드 폰에 개발자 모드가 활성화되어 있어야 한다.이 부분은 간단하고 검색하면 잘 나오므로 따로 다루지 않겠다.
안드로이드와 데스크탑이 같은 와이파이에 연결되어 있어야 한다.다른 네트워크에 연결되어있다면 무선 디버깅은 불가능하다.
1. 페어링 정보 생성
안드로이드 디바이스와 데스크탑을 연결하기 위해선 먼저 두 기기를 페어링 시켜 주어야 한다.
이를 위해 안드로이드에서 설정 > 개발자 옵션에 들어간다.
개발자 옵션에서 무선 디버깅을 활성화시킨다.
무선 디버깅을 클릭하여 들어가면 기기의 정보와 함께 다음과 같이 두 가지 페어링 옵션이 있다.
이 중 페어링 코드로 기기 페어링을 선택한다.
QR 코드 옵션은 터미널 환경에서 제공되지 않는 것 같다.
그러면 다음과 같이 페어링을 위한 코드와 IP 주소 및 포트가 표시된다.
이 정보는 앞서 표시된 기기 정보와 다르다는 것에 주의하자.
2. 페어링
이제 데스크탑으로 돌아와 명령 프롬프트(혹은 터미널)를 실행시켜준다.
adb pair <IP주소>:<포트>를 입력한다.
바로 위에서 확인한 페어링을 위한 IP 주소와 포트를 넣으면 된다.
정상적으로 입력했다면 위 스크린샷과 같이 성공 메시지가 출력된다.
다시 안드로이드를 확인해보면 페어링된 기기에 데스크탑이 표시되는 것을 확인할 수 있다.
그러나 아직 실제 연결은 되지 않은 상태이다.
페어링은 두 기기가 서로의 존재를 알게 해주는 것 뿐, 연결시키는 과정은 아니다.
adb devices 명령어로 연결된 안드로이드 디바이스를 확인해보면 아무것도 출력되지 않는다는 것을 알 수 있다. \
대신 한 번 존재를 확인시켜주었으니 다음에 무선 연결을 할 때에는 별도의 페어링 과정이 필요하지 않다.
3. 연결
실제 연결은 기기 정보를 이용해 adb connect <IP주소>:<포트> 명령으로 할 수 있다.
페어링에 사용했던 포트와 달리, 여기에 들어가는 정보는 무선 디버깅 화면에 표시된 기기 정보이다.
이를 수행하면 다음과 같이 무선 디버깅이 연결되었다는 알림이 뜬다.
이제 유선으로 연결한 것과 똑같이 프로젝트를 실행하고 디버깅할 수 있을 것이다.
02025. 01. 04.
일상
요즘 IT에 2024년 개발자 회고 글을 쓰며 느낀 점
https://yozm.wishket.com/magazine/detail/2907/
12월 27일에 내가 쓴 2024년 개발자 회고 글이 요즘 IT에 올라갔다.
개인적으로 올해는 더 나은 개발자가 되기 위해 깨달은 바가 조금은 있었기에 여기에 집중하며 글을 써보았다.
회고 글을 쓰면서 생각한 점을 여기에 풀어보고자 한다.
글의 방향 차이
지금까지 내가 써왔던 글은 정보 전달이 주 목적이었다.
처음 출판했던 코딩 테스트 책이나 지금 집필 중인 책, 그동안 요즘 IT에 기고했던 글이나 블로그에 올리고 있는 글까지 모두 내가 생각하는 것을 잘 전달하기 위한 글이었다.
회고 글도 큰 목적은 마찬가지이겠지만 조금 다르게 느껴졌다.
정보 전달보다는 내 경험을 공유하고, 여기서 배운 점을 전달하는 것이 위주가 되었다.
내가 알고 있는 것에 대해서 서술하는 것이 아니라 내가 새로 깨달은 것에 대해 이야기하려다보니 글을 쓰는 것이 어려웠다.
심지어 회사에서 배운 경험들은 구체적인 예시를 들 수도 없었기에 글이 점점 더 추상적으로 써지는 것 같았다.
2025년 목표에 대해서 쓸 때에도 마찬가지였다.
직접 경험해 본 것이 아니라 실험적으로 해보는 것이기에 구체적인 사례를 근거로 제시하기가 힘들었다.
그러나 이것은 이 글이 지금까지 써왔던 글과는 달리, 미래지향적인 글임을 의미한다.
그저 내 지식을 전달하는 것을 넘어서 내 생각을 정리하고 앞으로의 목표도 정할 수 있는 도전적인 성격의 글이었기에 매우 좋은 경험이 되었다.
AI와 개발자
최근 제미나이로 지뢰 찾기 사이트 만들기라는 포스트를 올렸다.
https://www.hyuni.dev/posts/1zUqcUuX7HcVp7NlSBMH
여기서 제미나이 2.0의 강력한 기능에 감탄했다.
확실히 AI가 코드를 작성하는 능력은 날이 다르게 발전하고, 웬만한 개발자들은 상대가 안될 것 같다고 느꼈다.
또, 요즘 IT에 쓴 개발자 회고 글에는 AI로 인해서 변한 것은 없다고 적었다.
이 생각은 아직도 같다.
개발자가 되기 위해서는 코드를 한 자 한 자 작성하는 것부터 공부하지만, 이것은 그저 가장 기초적인 역량일 뿐이다.
개발자는 그저 코드를 작성하는 것에서 멈춰서는 안된다.
아니, 오히려 코드를 작성하는 것은 그렇게 중요하지 않다.
실력 있는 개발자가 되기 위해서는 전체적인 흐름을 볼 수 있어야 한다.
프로젝트가 해결하고자 하는 문제를 이해하고, 그 원인을 파악해 해결할 수 있어야 한다.
프로젝트로 인해 파생되는 결과와 이것이 사용자에게 어떤 영향을 끼칠지에 대한 인사이트가 있어야 한다.
이것이 2024년 말에 깨달은 내가 생각하는 훌륭한 개발자의 지향점이고, AI의 등장으로 인해 이 지향점은 흔들리지 않는다.
그러나 나는 이러한 역량이 매우 부족하다.
프로젝트 규모가 조금만 커지거나 기술 스택이 복잡해지면 눈 앞의 일을 처리하기에 급급하다.
제대로 이해해보려고 시도하는 와중에 프로젝트는 빠르게 진행되어 놓치는 부분이 많다.
이를 보완하기 위해 문서를 작성하기 시작했다.
내가 이해한 바를 정리하고, 팀원분들이 이를 읽으면서 리뷰하는 과정에 잘못 이해하거나 놓치고 있는 부분이 있으면 금방 고칠 수 있다.
2025년에는 이러한 지향점을 바탕으로 조금 더 리더십과 프로젝트 인사이트가 있는 개발자가 될 수 있으면 한다.
02025. 01. 02.
일상 > 뉴욕 출장기
7일차 - 배터리 파크, 피자
뉴욕 출장의 마지막 날이다.
뉴욕 오피스의 팀원들과 자전거를 타고 맨해튼 남부까지 갔다.
오전 7시 30분 기상
마지막 날의 아침이 밝았다.
구름이 많이 끼고 날이 흐려 눈이 온 것 같은 분위기다/
오전 9시 30분 아침
역시 오피스에서 아침을 먹었다.
베이컨 오믈렛, 에그 스크램블, 소시지, 감자, 그리고 부리또이다.
부리또에는 베이컨과 계란, 치즈, 감자가 들어가있는 듯 하다.
사실 잘 기억이 안난다.
오후 5시 30분 자전거 타기
일과 후 뉴욕 팀원들이랑 자전거를 타기로 했다.
맨해튼 서쪽 강변을 따라서 남쪽으로 내려갔다.
자전거로 어느 정도 이동한 후 걷기 시작했다.
맨해튼 남서쪽에 위치한 복합 시설로, 상가와 지하철이 연결되어 있다고 한다.
들어가보지는 않았다.
오후 6시 40분 저녁
저녁으로는 피자를 먹었다.
Inatteso Pizzabar 라는 곳이었다.
세 판을 시켰는제 각 메뉴가 어떤 것인지는 정확히 기억나지 않는다.
그저 메뉴에 적힌 재료를 보고 추정만 해보았다.
오후 7시 30분 둘러보기
식사를 마치고 근처를 조금 더 둘러보았다.
해가 지고 있는데 이 시간까지 밖에 있어본 적이 없어서 무서웠지만 현지인이 함께 있으니까 크게 걱정되지는 않았다.
그런데 한 분에게 위험한 적 없었냐고 물어봤는데 갑자기 길 가다가 얼굴에 펀치를 맞은 적이 있다고 했다.
몇 년 전 이야기이긴 한데, 센트럴 파크 쪽에서 걷는 중에 한 커플의 남자가 갑자기 주먹을 날리고 웃으며 지나갔다고 했다.
확실히 이상한 사람은 많구나.
911 테러를 추모하기 위한 박물관이다.
오후 8시에 마감하는데 우리는 5분 전에 도착해서 얼른 밖에서 사진만 찍고 나왔다.
다시 오피스 근처로 왔다.
이렇게 늦게까지 밖에 나와 있다니.
생각보다 막 위험하다는 느낌은 들지 않았다.
뉴욕하면 치즈 케이크이다.
치즈 케이크로 유명한 매그놀리아 베이커리를 방문했다.
하지만 가장 인기 있는 오리지널 치즈 케이크는 다 팔리고 없어서 카라멜 피칸 치즈케이크를 샀다.
오후 10시 40분 공항 도착
인천행 비행기가 오전 1시이다.
2시간 반 정도 일찍 뉴어크 공항에 도착해서 탐승 수속을 했다.
팀원분이 비행기에서 잘 자라고 멜라토닌 초콜릿을 사다주셨다.
한 알에 1mg으로 적은 멜라토닌이 들어있는데 이런건 처음 먹어봐서 미지에 대한 두려움에 먹지는 않았다.
한국에 돌아와서 먹어봤는데 그냥 초콜릿이고 잠이 잘 오는 것도 모르겠다. 너무 소량인 듯 하다.
올 때 처럼 기내식을 맥주와 함께 먹었다.
이 때는 파우치는 안줬다.
두 번째 기내식이다.
저 오른쪽 위 초코 케이크가 부드럽고 맛있었다.
잠을 자다 깨다 하면서 심심할 때 책을 썼다.
팀원분들을 포함한 회사 사람들에게 보여주기는 부끄러웠지만 자리가 떨어져있어서 중간 중간 쓸 수 있었다.
이렇게 일주일간의 첫 뉴욕 출장이 막을 내렸다.
처음에 적응하는데 시간이 걸리고, 시간과 체력 한계 때문에 못 해본 것도 많지만 재미있고 유의미한 시간이었다.
특히 한국에서만 일을 하다가 미국에 나가 일을 하니 새삼 구글이라는 회사의 규모가 체감되었다.
내가 하고 있는 일도 그저 흘러가는 것이 아니라 조금 더 책임감을 가져야겠다는 생각과 함께, 형제 팀들에서 진행 중인 다양한 프로젝트를 보면서 시야도 넓어질 수 있었다.
이 때의 경험들을 기반으로 소프트웨어 엔지니어로서 발전시켜야 할 역량이 더욱 확실해진 느낌이다.
02024. 12. 30.
일상 > 뉴욕 출장기
6일차 - 브로드웨이 위키드 뮤지컬, 르뱅 쿠키, 스시
오랜만에 이어 쓰는 뉴욕 출장기..
사진을 보며 당시 기억을 떠올리면서 써본다.
특히 이 날은 요즘 화제의 영화 위키드의 현지 브로드웨이 뮤지컬 버전을 본 날이다.
이 포스트를 일찍 썼어야 하는데...
오전 8시 30분 르뱅 쿠기
르뱅 쿠키는 한국에서 크고 두꺼운 쿠키의 종류로 알려져 있지만, 사실 미국 뉴욕의 Levain Bakery라는 곳에서 파는 쿠키이다.
https://levainbakery.com/
이곳의 쿠키가 워낙 독특하고 맛있어서 한국에서 르뱅 쿠키 스타일의 쿠키를 따라 만들며 쿠키의 한 종류처럼 유행하기 시작했다.
Levain Bakery는 뉴욕에만 여러 종류가 있는데, 그 중 가장 큰 곳은 쿠키를 사기 위해 줄을 서서 기다려야 할 정도로 인기가 많다고 한다.
우리는 숙소에서 오피스를 가는 길에 작은 지점이 있어서 르뱅 쿠기를 포장해 오피스에서 아침과 함께 먹기로 했다.
오전 9시 아침
르뱅 쿠키를 포장해서 오피스에서 아침을 먹었다.
실외 테라스에 자리를 잡고 앉았는데, 쿠키가 있어서 나머지 음식은 그렇게 많이 담지는 않았다.
토스트와 스크램블 에그, 빵 하나와 작은 소시지 한 조각을 담아 왔다.
음료는 오렌지 주스이다.
뉴욕 오피스의 조망이 좋다고 들었고, 월요일에 오피스 투어를 하면서 봤지만 실외에서 아침을 먹으며 보는 경치는 또 달랐다.
완벽한 날씨에서 그늘진 곳에 자리를 잡아 완벽한 아침을 먹을 수 있었다.
아침을 먹고 있는 팀원들을 뒤로한 채 창피함을 무릅쓰고 셀카를 찍었다.
아침을 먹은 후 커피와 함께 르뱅 쿠키를 먹었다.
나는 다크 초콜릿 쿠키를 골랐는데 아주 달고 칼로리 높은 맛이었다.
한 번에 다 먹기는 힘들어서 조금 남겼던 것 같다.
오후 12시 점심
점심은 뉴욕 팀 사람들과 함께 피어 오피스에서 먹었다.
피어 오피스에 대한 내용은 이전에 작성했던 오피스 투어 포스트에서 찾아볼 수 있다.
https://www.hyuni.dev/posts/iGsBxcX6PtrYUDhd8t0k
나는 해물로 만든 전 같은 걸 먹었는데 간이 좀 이상했다.
모든 음식이 너무 짰다.
심지어 사진 왼쪽에 있는 샐러드조차 소금 범벅인듯 했다.
과일은 맛있었다.
오후 5시 30분 모모야 첼시
위키드 뮤지컬을 보러 가기 전 저녁으로 스시를 먹기로 했다.
브로드웨이로 가는 길에 있는 모모야 첼시 (Momoya Chelsea)라는 곳을 방문했다.
https://momoyanyc.com/chelsea.html
다 같이 먹을 수 있는 모듬 스시를 주문했는데, 정확한 메뉴는 기억이 안나니 사진만..
가장 인상 깊어서 기억에 남은 스시는 캘리포니아 롤이다. 모듬 스시 2에서 가장 오른쪽에 있는 빈약한 롤이 캘리포니아 롤이었던 것 같다.
한국에서의 캘리포니아 롤은 뭔가 가득가득 들어있어서 터질 것 같은 경우가 많은데 여기는 그렇지 않았다.
뉴욕이라 캘리포니아 이름이 들어간 것에는 힘을 뺀 건가 싶었는데, 검색해보니 원래 캘리포니아롤은 아보카도, 오이, 게 맛살만 들어간다고 한다.
4명이서 먹었는데 음식 값이 $158.96, 팁으로 $30를 내서 총 $188.96을 지불했다. 현재 환율로 약 27만 7천원이다.
오후 6시 50분 브로드웨이 극장
위키드(Wicked) 뮤지컬을 보러 브로드웨이로 향했다.
극장은 보안과 경비가 철저했다.
모든 입장객이 금속 탐지기를 통과해야 했다.
500석 이상의 좌석이 있는 브로드웨이에서 총기사고라도 났다간 대참사일 것이다.
위 사진에서 왼쪽 아래 노란색으로 표시된 곳에 앉았다.
이 위치의 좌석에서는 이 정도 뷰가 나왔다.
웅장한 무대 세팅이 들어가자마자 시선을 사로잡았다.
아무래도 영어라 모든 대사를 알아듣기는 힘들었지만, (특히 노래는 80% 이상 못 알아들었다) 내용은 따라갈 수 있었다.
2 부로 나뉘어 진행됐는데 상당히 재미있었고, 왜 사람들이 뮤지컬을 보러 다니는지 알 것 같았다.
뮤지컬 가격을 보기 전까지는...
브로드웨이 위키드 뮤지컬 가격
뮤지컬을 예매할 때 분명 가격을 들었다.
그런데 달러였는지 체감이 안됐었나보다.
나중에 한국에 들어와서 정산할 때 보니 정산해야 할 금액이 생각보다 많았다.
그렇게 쓴 게 없는 것 같은데 뭐지 하고 보니까 뮤지컬이 거의 전부였다.
당시 가격으로 $158.50 이었으니 20만원이 넘는 가격이다.
재밌긴 했지만... 그정돈가...?
이런 교양 문화와 멀리 떨어져 있는 나는 한 번으로 족한 경험인 것 같다ㅋㅋ
뮤지컬을 마지막으로 이 날은 마무리되었다.
02024. 12. 30.
프로그래밍
제미나이로 지뢰 찾기 사이트 만들기
제미나이 2.0은 매우 강력한 성능을 가지고 있다.
현재 2.0은 실험적으로 공개된 상태인데, 다음의 두 모델이 공개되어 있다.
무료 버전인 Gemini 2.0 Flash
유료 버전인 Gemini 2.0 Advanced
제미나이 2,0은 이전 버전에 비해서 자연어 이해는 물론, 코드 생성 능력도 비교할 수 없을 만큼 향상되었다고 느꼈다.
이전 버전의 제미나이는 코드를 생성했다 하면 다음 문제점 중 하나를 가지고 있었다.
컴파일 되지 않는 코드
이전 버전의 코드
원하는 기능이 누락된 코드
제미나이 2.0은 이러한 점들이 대폭 개선되어 몇 번의 코드 생성만으로 거의 모든 원하는 결과를 얻을 수 있게 되었다.
지뢰 찾기 만들기
제미나이 2.0의 향상된 기능을 테스트해보고자 지뢰 찾기를 만들어 보았다.
이번 경험으로 제미나이를 활용한 개발에 대한 감을 잡을 수 있을 것이다.
1. 첫 코드 생성
맨 처음 다음과 같이 살짝 무책임하게 보일 수도 있는 프롬프트를 입력했다.
" html / css / js로 지뢰찾기 만들어줘.
제미나이는 index.html, style.css, script.js 파일을 생성해 주었다.
이를 복사해서 넣어봤는데, 아무런 오류가 없었다..!
그리고 실행 화면도 놀라웠다.
상당히 깔끔하게 스타일을 입혀 놓았다.
배경 색과 지뢰 찾기 판의 색, 버튼 색까지 어색하지 않다.
기능도 잘 동작했다.
클릭으로 해당 칸 확인, 우클릭으로 지뢰를 표시할 수 있다.
왼쪽 위에는 첫 클릭 기준으로 게임 플레이 시간이 표시되며, 오른쪽 위에는 찾은 지뢰의 개수가 표시된다.
모든 지뢰를 다 찾으면 게임 승리 창도 띄워준다.
아래 난이도 버튼을 통해서 판의 크기를 조절할 수 있다.
Beginner는 9 x 9 칸에서 10개의 지뢰를,
Intermediate은 16 x 16 칸에서 40개의 지뢰를,
Advanced는 30 x 16 칸에서 99개의 지뢰를 찾아야 한다. (해보니 지뢰가 너무 많은 것 같아 75개로 줄였다)
지뢰도 매번 랜덤으로 심기 때문에 중복 게임이 발생하지 않는다.
2. 지뢰 찾기 판 가운데 정렬
그런데 한 가지 걸리는 것이 있다.
다른 난이도에서는 괜찮은데, Beginner일 때 지뢰 찾기 판이 왼쪽으로 치우쳐져 있다.
이것을 수정해달라고 요청해보자.
" Intermediate나 Advanced에서는 지뢰 찾기 판이 가운데 잘 있는데, Beginner에서는 왼쪽으로 치우쳐져있어. 제목이나 버튼 같은 다른 요소들은 괜찮은데 지뢰 찾기 판만 그래. 수정해줘.
제미나이 2.0은 성공적으로 원인을 찾아 수정 사항을 제시해 주었다. \
table {
border-collapse: collapse;
box-shadow: 0 0 10px rgba(0, 0, 0, 0.3);
background-color: #eee;
margin: auto; /* 이것을 추가하여 테이블을 중앙에 정렬 */
}
복사하기 편하게 전체 코드도 제공해 주었다.
제시된 수정 사항을 반영하여 다시 실행해보니, 원하는 대로 가운데에 지뢰 찾기 판이 정렬되게 되었다.
휠 클릭으로 인접 칸 열기
지뢰 찾기 게임에는 휠을 클릭하여 주변 지뢰를 모두 찾은 숫자 칸 주변을 자동으로 오픈하는 기능이 있다.
이를 구현하기 위해 다음과 같이 프롬프트를 추가로 입력했다.
" 원래 지뢰찾기는 다음과 같은 편의 기능이 있어. "공개된 숫자 칸에 마우스 휠 버튼으로 클릭한 경우, 만약 해당 숫자 칸으로 인한 지뢰에 전부 깃발 표시를 한 상태이면, 해당 숫자 칸 주변의 8칸 중 나머지 칸을 자동으로 클릭하여 오픈." 이 기능을 구현해줘
제미나이는 코드를 뱉었고, 이를 적용해 보았다.
안타깝게도 코드에는 문제가 있었다.
마우스의 휠 클릭이 아니라, 휠을 돌렸을 때 해당 기능이 동작했다.
사실 몇 번 해보니 휠을 클릭하는 것보다 돌리는게 훨씬 편하긴 했지만, 원하던 방향은 아니니 다시 프롬프트를 입력했다.
제미나이는 다음과 같은 대답을 하며 수정된 코드를 알려 주었다.
휠을 "돌렸을 때"가 아닌 "클릭했을 때" 기능이 동작하도록 수정해달라는 요청을 정확히 이해했습니다.
wheel 이벤트는 마우스 휠을 스크롤할 때 발생하기 때문에, 휠 클릭을 감지하려면 mousedown 이벤트를 사용하고 event.button 속성을 확인해야 합니다. event.button 값이 1이면 휠 클릭을 의미합니다.
script.js에서 다음과 같이 수정합니다.
그리고 이 코드를 적용하니 휠을 클릭했을 때 주변 칸이 열리는 기능이 정상적으로 동작하였다.
3. 제미나이 2.0을 써보니...
제미나이 2.0이 공개되면서 코드 생성 성능 또한 매우 강력해졌다.
이번에 특히 느낀 것은 다음의 네 가지다.
코드에 버그가 없다.물론 완벽히 없을 수는 없겠지만 이번 지뢰 찾기 정도 수준에서는 찾아볼 수 없었다.
코드를 확인하지 않고 그대로 복사 붙여넣기만 했는데도 원하는 기능이 만들어졌다.
기억력이 좋아졌다.여러 차례 대화가 오갔음에도 처음 생성했던 코드 기반으로 업데이트를 해 나갔다.
기능이 추가되면서 수정된 코드나 처음의 코드를 잊어버릴 법 한데 원하는 수정을 다 할 때까지 누락된 것이 없었다.
이해를 잘 한다.내가 원하는 것을 파악하고 코드로 옮겨 주었다.
휠 클릭과 굴리는 것을 혼동하기는 했지만, 기능 자체는 매우 잘 구현하였고, 수정을 요청했을 때 바로 알아듣고 성공적으로 수정하였다.
답변이 길어졌다.이전에는 답변이 조금 길어진다 싶으면 에러를 뱉고 뻗어버리는 경향이 있었는데, 지금은 상당히 긴 답변을 한다.
지뢰 찾기를 작성하면서 부분적으로 코드를 수정할 때에도 수정된 부분을 보여주고, 이어서 전체 코드를 한 번 더 보여주었다.
이렇게 강력해진 제미나이를 활용하면 코드 작성에는 확실히 신경을 덜 쓸 수 있을 것이다.
앞으로 더욱 프로젝트의 방향성과 논리적 사고에 집중하며 실력 있는 개발자로서의 역량을 키워나갈 수 있을 것 같다.
이번에 작성한 지뢰 찾기 코드는 내 깃헙 Playground 리포지토리에서 찾아볼 수 있고, 다음 링크에서 실제로 해볼 수 있다.
https://playground.hyuni.dev/minesweeper/
02024. 12. 27.
프로그래밍
SPA (Single Page Application)의 장단점 - 웹 퍼블리셔와 프론트엔드 개발자
웹 퍼블리셔라는 말을 들어본 적 있을 것이다.
이 용어는 디자인된 페이지를 그대로 HTML / CSS / JS로 옮기는 작업을 하는 사람들을 일컫는다.
얼핏 들으면 프론트엔드 개발자와 같은 역할인 것 같다.
실제로 이러한 인식 때문에 프론트엔드 개발자들이 백엔드 개발자보다 실력 없는 개발자라는 이야기가 많이 있었다.
그러나 웹 개발이 발전해 나감에 따라 웹 퍼블리셔가 없어지고 프론트엔드 개발자가 등장하게 된 데에는 이유가 있다.
이것을 이해하기 위해서는 과거의 웹 개발이 어땠는지 살펴보고, 웹 개발에 획기적인 전환점을 불러일크킨 SPA (Single Page Application)에 대해서 알아볼 필요가 있다.
과거의 웹 개발
전통적인 웹 개발은 백엔드 개발에 많은 부분 얽매여 있었다.
웹 사이트는 여러 개의 HTML 페이지로 구성된 MPA (Multi-Page Application) 형태였으며, 새로운 페이지를 요청할 때마다 서버는 매번 새로운 HTML 파일을 생성하여 브라우저에 전송했다.
즉, 모든 페이지의 렌더링이 서버에서 이루어지는 서버 사이드 렌더링 (Server-Side Rendering) 방식이었다.
이러한 구조에서 Javascript는 주로 폼 유효성 검사나 간단한 시각 효과를 위한 보조적인 역할에 머물렀다. 간혹 api 요청 등 비동기 작업이 있다고 하더라도 대부분의 로직은 서버에서 처리되었기 때문에, 프론트엔드 개발자의 역할은 상대적으로 제한적일 수 밖에 없었다.
과거 웹 개발 방식 (MPA)의 문제점:
느린 페이지 로딩새로운 페이지를 요청할 때마다 전체 페이지를 다시 로드해야 했기 때문에 속도가 느리고 사용자 경험이 좋지 않았다.
아예 새로운 페이지를 로딩하는 것은 감안하더라도, 페이지의 일부분만 업데이트 할 때도 페이지 전체를 새로 로드해야 했다.
높은 서버 부하모든 페이지 요청에 대해 서버가 전체 HTML을 생성해야 하므로, 서버 부하가 높고 많은 양의 데이터가 전송되어야 했다.
제한적인 상호작용사용자와의 상호작용이 많은 웹 애플리케이션을 구현하기 어려웠다.
부드러운 페이지 전환은 불가능했고, Javascript의 비중이 많은 페이지를 개발하는 것도 쉽지 않았다.
복잡한 상태 관리여러 페이지에 걸쳐 애플리케이션의 상태를 관리하는 것이 번거로웠다.
SPA의 등장
이러한 문제점을 해결하기 위해 등장한 것이 바로 SPA (Single Page Application) 이다.
SPA는 이름 그대로 단 하나의 HTML 페이지를 기반으로 하는 웹 애플리케이션이다.
(간혹 여기서 오해하는 경우가 있는데, 개발은 여러 HTML 페이지로 한다. SPA는 이를 webpack으로 묶어 하나의 HTML 파일로 빌드한다.)
React.js, Angular, Vue.js와 같은 프레임워크 및 라이브러리가 SPA를 구현하기 위해 대표적으로 사용되며, 최초 로드 시 하나의 HTML 페이지만을 받고, 이후에는 Javascript를 사용하여 동적으로 콘텐츠를 변경하는 클라이언트 사이드 렌더링 (Client-Side Rendering) 방식을 사용한다.
SPA는 사용자와의 상호작용에 따라 필요한 데이터만 서버로부터 비동기적으로 가져와(AJAX, Fetch API 등) 화면의 일부분만 업데이트한다.
따라서 전체 페이지를 다시 로드할 필요가 없기 때문에, 훨씬 빠르고 부드러운 사용자 경험을 제공할 수 있다.
SPA의 장점
빠르고 반응성 좋은 사용자 경험페이지 전체를 다시 로드하지 않기 때문에, 부드러운 화면 전환과 빠른 반응 속도를 제공한다.
서버 부하 감소필요한 데이터만 요청하고 클라이언트 측에서 렌더링을 수행하기 때문에, 서버 부하를 줄일 수 있다.
코드 재사용성 및 유지보수 용이컴포넌트 기반 아키텍처를 통해 코드의 재사용성을 높이고 유지보수를 쉽게 할 수 있다.
SPA의 장점은 그 무엇보다 사용자 경험이 크게 향상된다는 것에 있다.
버튼을 클릭할 때 마다 페이지 전체가 로딩되던 과거와 달리, 버튼을 누르자마자 페이지가 부드럽게 전환되고, 데이터가 로드되면 자연스럽게 보여주는 방식은 SPA를 사용하는 브랜드 자체를 더욱 친근하고 고급스럽게 만들었다.
SPA의 대표격인 리액트의 수요가 크게 증가했으며, 단순히 디자인 된 것을 코드로 옮기기만 하는 웹 퍼블리싱보다 더욱 높은 기술적 난이도가 요구되었다.
부드러운 사용자 경험이 안정적인 서비스만큼 중요해지면서 프로젝트에서 Javascript의 비중이 함께 증가했고, 재사용성 높은 컴포넌트를 설계하고 복잡한 프로젝트를 오류 없이 관리해나가는, "엔지니어"의 역량이 필요해진 것이다.
이 때 부터 퍼블리싱 보다는 더욱 사용자와 가까이서 그들을 이해하고, HTML, CSS, Js를 넘어 여러 라이브러리와 프레임워크를 활용하여 알맞는 기술적 솔루션을 구현해내는 프론트엔드 개발자가 등장하기 시작하고, 프론트엔드 기술도 한층 박차를 가해 발전하기 시작했다.
SPA의 단점
초기 로딩 속도초기에 모든 Javascript 파일을 로드해야 하기 때문에 초기 로딩 속도가 느릴 수 있다.
SEO (검색 엔진 최적화) 문제검색 엔진 크롤러가 Javascript를 실행하지 못하는 경우, 콘텐츠를 제대로 수집하지 못할 수 있다.
대부분의 최근 검색 엔진 크롤러는 SPA를 고려하여 Javascript를 실행한 후, 콘텐츠가 로드되면 크롤링을 한다.
보안클라이언트 측에서 많은 로직이 처리되기 때문에 보안에 더 신경 써야 한다.
높은 사용자 친화적 경험을 제공해서 각광받았던 SPA는 시간이 지남에 따라 그 단점 또한 부각되었다.
대부분의 단점들은 SPA가 발전해나감에 따라 같이 해결되었지만, 기술적 한계로 인해 그렇지 못한 것들도 있다.
초기 로딩 속도 같은 경우, 사이트 전체에서 사용될 코드를 전부 초기 로딩 시에 불러오기 때문에 느릴 수 밖에 없다.
한 번 로드된 이후부터는 매우 빠르게 페이지를 전환할 수 있다는 장점에 대한 트레이드 오프이다.
보안은 각별히 신경써야 한다.
대부분의 로직이 서버에서 돌아가던 과거와 달리, 클라이언트에서 돌아가는 로직은 전부 공개된 것이나 다름 없다.
SPA를 구동하기 위한 Javascript는 브라우저에서 실행되어야 하기 때문에 브라우저의 개발자 모드를 열어보면 전부 까볼 수 있다.
난독화 과정을 거치기는 하지만 마음만 먹으면 읽을 수 있기 때문에 안전하다고는 할 수 없다.
Javascript에서 사용하는 API 키나 비밀번호 같은 중요한 정보도 모두 공개되기 때문에 중요한 정보는 노출시키지 않도록 세심한 주의가 필요하다.
SPA는 분명 장점과 단점을 모두 가지고 있으며, 이러한 단점을 보완하기 위한 차세대 라이브러리와 프레임워크 또한 많이 등장했다.
그러나 사용자에게 더 나은 경험을 제공하고, 개발 생산성을 향상시킬 수 있는 잠재력이 크기 때문에, 현대 웹 개발의 핵심 기술로 자리 잡았다.
SPA의 단점을 보완하는 Next.js 등과 같은 프레임워크도 React.js 기반이므로 React.js와 SPA의 장단점을 명확히 파악한다면 Next.js가 어떤 문제를 풀기 위해 탄생했는지, 그로 인해 발생하는 Next.js의 장단점은 무엇인지 또한 자연스럽게 알 수 있을 것이다.
02024. 12. 27.
일상
나의 세 가지 글 쓰기 - 블로그, 요즘 IT, 그리고 책
나의 첫 번째 책 취업과 이직을 위한 프로그래머스 문제 풀이 전략: 자바편을 출간한 후로, 글을 자주 쓰게 되었다.
https://www.hyuni.dev/posts/qqK2tlLCrOyYAuahj8FY
https://www.hyuni.dev/posts/6DfarGbSppjAMB2AHkY6
확실히 책 하나를 목표로 잡고 달렸던 경험이 글을 쓰는데 있어서 큰 도움이 된 듯 하다.
나는 지금 세 군데 글을 쓰고 있다.
블로그
요즘 IT
책
이번 포스트에서는 이 세 매체에 대한 나의 생각을 정리해보고, 이를 기반으로 각 매체에 어떤 성격을 글을 위주로 쓸지를 정해보려 한다.
각 매체 성격 분석하기
우선 세 매체에서 다루는 글의 성격과 독자층에 대해 생각해보자.
1. 블로그
https://www.hyuni.dev
블로그는 온전한 나의 공간이다.
내가 작성하고 싶은 주제와 내용으로 마음껏 글을 쓸 수 있으며, 분량 제한도 없다.
심지어 지금 운영 중인 블로그는 개발까지 내가 하고 있어 블로그의 시스템과 연계한 글도 작성할 수 있다.
나만의 공간이고 별도의 홍보도 하지 않으므로 방문 수가 적어도 별로 신경 쓰이지 않는다. 오히려 그것이 당연하다고 생각한다.
한글로만 작성된 개발 블로그에 대한 수요는 그렇게 많지 않을 것이다.
이러한 성격의 블로그가 높은 조회수를 기록하기 위해서는 트렌딩한 주제를 들고 오거나 물량으로 승부를 봐야 할 것이다.
그러나 블로그 글의 주제를 찾으려 고군분투하며 스트레스 받고 싶지 않기 때문에 공유할만한 주제가 있을 때마다 기록해두고, 포스트로 작성하는 것이 좋을 것 같다.
블로그의 독자층은 매우 다양하다.
전문적인 정보를 검색하는 사람들도 있을 것이고, 프로그래밍 초기에 자주 접하는 에러를 검색하다가 내 블로그를 접하는 사람들도 있을 것이다.
이들의 공통점은 원하는 정보가 명확하다는 것이다.
길게 늘어진 정보 보다는 찾고자 하는 정보에 대한 답을 빠르게 얻을 수 있는 글을 선호한다.
2. 요즘 IT
https://yozm.wishket.com/magazine/@spaceship00/
요즘 IT는 구글 문서 기준 약 5 페이지 정도의 분량의 단편적인 글을 위주로 기고한다.
주제 제안 후 원고 집필을 하게 되고, 검토와 교정을 거친 후 요즘 IT에 등재된다.
요즘 IT의 장점은 독자층이 많다는 것이다.
내가 지금까지 요즘 IT에 기고한 4개의 글 중 가장 조회수가 적은 글도 조회수가 7천 이상이다.
요즘 IT는 주니어 레벨 독자층이 많은 듯 하다.
사실 나는 내가 기고한 글 중 위의 글이 개발자에게 있어서 가장 중요한 글이라고 생각한다.
논리적 사고로 문제를 해결하는 과정을 직접 따라가 보는 것은 논리적 사고의 흐름에 대한 시야를 틔워줄 수 있는 계기가 될 수 있을 것이라 생각하기 때문이다.
그러나 기고한 다른 글들, 이를테면 "코딩 테스트 준비 팁"이나 "코드 스타일의 중요성"과 같은 글이 훨씬 높은 조회수를 기록했다.
아무래도 이러한 글들은 조금 더 직관적이고 이해하기 쉬운 내용이어서 그런 것 같다.
3. 책
책에 들어가는 글은 가장 집중해서 써야 하는 글이다.
책은 한 번 인쇄 후에는 수정이 불가능하고, 분량도 매우 많다.
종이책이라는 현물을 만들어 내는 것이기에 리스크도 크고 도전적이다.
그러나 그만큼 따라오는 보상도 크다.
내가 이렇게 블로그와 요즘 IT에 글을 쓰고 있는 것도 첫 번째 책을 집필했기 때문이 크다.
글을 쓰는 것의 힘을 알게 되었고, 나의 생각을 글로 표현하는 것의 재미를 느끼게 되었다.
첫 번째 책을 쓸 기회를 얻지 않았다면 지금 이렇게 글을 쓰고 있는 시간에 나는 무엇을 하고 있었을까?
책은 확실한 독자층을 설정해 놓아야 한다.
그리고 그 독자들 입장을 최대한 생각하며 글을 작성해야 한다.
글은 독자들이 천천히 이해할 수 있도록 내용을 유기적으로 연결시켜 써서 그저 정보를 모아놓은 문서 덩어리가 되지 않도록 주의해야 한다.
앞으로 내가 쓸 글
세 매체의 성격이 매우 다르므로 각 매체에 쓸 글의 성격도 다를 것이다.
블로그가벼운 글
단편적인 정보 전달 글
블로그의 기능과 연계하여 쓰는 글
요즘 IT어느 정도 분량이 있는 글
나의 인사이트를 공유하는 글
개발자들에게 일반적으로 적용되는 글
책책의 주제와 유기적으로 연결되는 글
나의 경험을 상세하게 풀어 공유하는 글
블로그는 쉽게 쓸 수 있지만 나 혼자의 만족으로 끝나는 경우가 많다.
요즘 IT는 주제와 분량에 어느 정도 제한이 있지만, 조회수나 댓글 등으로 즉각적 피드백을 받을 수 있다.
책은 가장 오래 걸리고 분량도 많지만 그만큼 한 번 출간했을 때 얻을 수 있는 것이 크다.
노린 건 아니지만 어떻게 하다 보니 세 매체가 서로 균형을 이루게 되었다.
이제 블로그와 요즘 IT, 책 집필의 역할이 모두 정해졌으니 글을 쓸 일이 생겼을 때 주저하지 않고 알맞은 곳을 선택하여 쓸 수 있을 것이다.
02024. 12. 26.
Next.js
Server Component와 Client Component 구분하기
내 블로그는 Next.js로 돌아간다.
포스트의 내용 중 링크가 있으면 Open Graph로 보여주는데, 이를 통해 해당 링크의 제목, 이미지 등 대표적인 내용을 보여줄 수 있다.
링크에서 Open Graph의 내용을 가져오려면 네트워크 요청을 보내야 한다.
그렇기 때문에 server component에서는 async 컴포넌트로 데이터를 가져온 후 렌더링해서 보내준다.
if (href != null && href === children?.toString()) {
return <OpenGraphBlock url={href} />
}
:: 기존의 서버 사이드 Open Graph 렌더링 컴포넌트 ::
문제는 포스트를 쓰는 중 "미리보기"를 할 때 발생했다.
미리보기는 포스트의 내용을 서버에서 렌더링하는 것이 아니라 클라이언트에서 가지고 있는, 현재 작성 중인 내용을 가지고 렌더링한다.
같은 Open Graph 컴포넌트를 사용하면 클라이언트 사이드에서 async 컴포넌트를 호출하게 되는 것이다.
이는 다음과 같은 에러를 발생시켰다.
Application error: a client-side exception has occurred (see the browser console for more information).
클라이언트 사이드에서 async 컴포넌트를 렌더링할 수 없어서 생긴 에러였다.
이 에러가 발생하는 것은 진작 알고 있었지만 어차피 게시글은 나 혼자 쓰는 것, 그냥 조금 조심하면서 쓰면 되지 하는 마인드로 미뤄놨었다.
그러나 링크를 많이 사용할 포스트를 작성할 일이 생겨, 수정하기로 했다.
이를 해결하기 위해서는 현재 컴포넌트가 서버 사이드에서 렌더링 되는지, 클라이언트 사이드에서 렌더링 되는지를 알아야 했다.
typedef window == 'undefined'
방법은 매우 간단했다.
window가 정의되어 있는지를 확인하면 됐다.
서버 사이드의 경우 window 객체가 없기 때문에 그 타입이 undefined이다.
이를 활용하면 undefined인 경우 서버 사이드, 그렇지 않은 경우 클라이언트 사이드임을 알 수 있다.
if (typeof window == 'undefined') {
return <OpenGraphBlockServer url={href} />
} else {
return <OpenGraphBlockClient url={href} />
}
:: 렌더링 위치를 구분한 Open Graph 컴포넌트 ::
이제 게시글을 작성할 때에도 링크 포함 여부 상관 없이 미리 보기를 보면서 작성할 수 있게 되었다.
02024. 12. 25.

일상
구글 드라이브로 이미지 호스팅하기 (<img>용 링크 변환)
지금껏 블로그에 올리는 이미지들은 대부분 파이어베이스 스토리지를 사용하고 있었다.
파이어베이스 무료 요금제로는 용량과 대역폭 제한이 있기 때문에 이미지를 올릴 때 원본을 올리기가 망설여졌다.
휴대폰으로 찍은 원본 이미지 몇 장만 들어가도 전송량이 너무 커지기 때문에 유료 요금제로 바꿔야 하나 싶었다.
그런데 나는 구글 드라이브 5TB 용량을 구독하고 있다. (회사 복지 아님. 돈 내고 쓰는 중)
아직 이 중 1.5TB도 사용하고 있지 않다.
구글 드라이브에 블로그 용 이미지를 저장하고, 그 링크를 이용하면 용량이나 대역폭 걱정 없이 이미지를 마음껏 넣을 수 있을 것 같아 알아본 방법을 공유한다.
이미지를 블로그에 넣으려면 태그의 src 속성에 넣을 수 있어야 한다.
그러나 구글 드라이브는 웹에서 들어갔을 때 얻을 수 있는 링크가 이미지 파일 자체 링크가 아닌, 이미지 뷰어의 링크이기 때문에 태그에 직접 넣어줄 수 없고, 변환을 해주어야 한다.
구글 드라이브에 이미지 저장용 폴더를 만들고 태그용 링크를 얻는 것 까지의 과정은 다음과 같다.
1. 이미지 저장용 폴더 생성
나는 블로그에 들어갈 이미지를 호스팅할 것이기 때문에 Blog 폴더 아래에 Images 폴더를 생성해주었다.
이 폴더에 있는 이미지들은 모두 공개되어야 한다.
다음과 같이 폴더에 우클릭 -> 공유 -> 공유 를 선택해준다.
공유 다이얼로그가 뜨면 일반 액세스에 링크가 있는 모든 사용자를 선택해 뷰어 권한을 준다.
2. 이미지 업로드
생성한 Images 폴더에 들어가 공유할 이미지를 업로드한다.
나는 블로그를 작성하면서 찍은 스크린샷들을 올려놓았다.
Images 폴더가 공유되어 있기 때문에 이 안의 이미지들은 자동으로 공개되어 있는 상태이다.
3. 이미지 링크
이미지를 태그에서 보여주기 위해서는 우선 이미지의 id를 알아야 한다.
이를 위해 이미지에 우클릭 -> 공유 -> 링크 복사를 선택한다.
그러면 다음과 같은 링크가 생성된다.
https://drive.google.com/file/d/1iV4jl41tIfLpSvwZdPpxryO2nkcCIq8u/view?usp=drive_link
이 중 가운데 부분이 이미지의 id이다.
1iV4jl41tIfLpSvwZdPpxryO2nkcCIq8u
이 것을 다음 링크 뒤에 붙여준다.
https://lh3.googleusercontent.com/d/{이미지 id}
그러면 다음과 같이 태그 안에 넣을 수 있는 이미지 링크가 된다.
<img src="https://lh3.googleusercontent.com/d/1iV4jl41tIfLpSvwZdPpxryO2nkcCIq8u" />
게시글을 쓸 때마다 이미지 용량이 걱정이었는데, 이제 마음껏 올릴 수 있게 되어서 마음이 편하다.
다만 매번 링크를 변환해주어야 하는 것이 번거로운데, 게시글 작성하는 페이지에 간단하게 변환 툴 하나 넣어놓아야겠다.
02024. 12. 24.

일상
맥 미니 M4 지른 날 (+ 내 데스트 셋업)
플러터를 담당하고 있는 사이드 프로젝트에서 iOS 빌드가 필요한 순간이 찾아왔다.
맥북을 가지고 있는 다른 사람에게 부탁해도 되겠지만 언젠가 나도 직접 iOS 빌드를 해야 할 거라는 생각에 맥 미니를 구입하기로 결정했다.
맥북을 구입하지 않은 이유는:
비싸다.
나는 노트북으로 작업하지 않는다. 큰 모니터가 필요하다.
어차피 집에 데스크탑 세팅은 다 되어 있으니 맥 미니 본체만 사서 연결하면 될 것이다.
빌드용이니 M4 기본형이면 충분하고도 넘치겠지.
애플 스토어 여의도점
결심한 순간 바로 애플 스토어 여의도점으로 달려갔다.
가격도 알아보고, 픽업도 가능하다는 것도 확인하고 갔다.
직원분에게 맥 미니 M4 기본형을 주문하고, 결제를 하기 위해 폰을 꺼내는 순간, 삼성 페이는 안된다는 청천벽력같은 소리를 들었다.
한국에서 삼성 페이가 안된다니... 동네 편의점에서도 되는걸...
일부러 막아놓았다고 밖에 생각할 수 없다...
실물 카드도 없고, 계죄이체도 안된다고 했다.
대신 현금은 가능해서 ATM에서 뽑아오는 방법이 있다더라..
ATM에서 출금할 카드도 없고, 내가 사용하는 신한 ATM도 못찾겠어서 온라인 주문 후 픽업을 하기로 했다.
모바일로 애플 스토어에서 주문을 넣은 후, 오프라인으로 픽업하러 오는 시스템인데, 직원분 말로는 이게 처리되려면 빠르면 5분, 느리면 2시간 까지도 걸린다고 했다.
딱히 대안이 없으니 빠르게 처리되길 빌면서 주문을 넣고 앉아서 기다렸다.
마침 스토어에서 아이폰 카메라의 편집 기능을 알려주는 세션이 있어서 그걸 보면서 시간을 때우던 중, 정신 없는 문자가 왔다.
주문을 넣은 후 10분 ~ 15분 정도 된 것 같다.
곧 이메일로도 픽업 QR이 도착했다.
이걸 직원분에게 보여주고, 패스로 신분증 확인까지 한 후에 비로소 맥 미니를 받을 수 있었다.
맥 미니 개봉
얼른 집에 와 상자를 개봉했다.
이렇게 작고 깔끔한 상자에 포장되어 있다.
뒤에는 상세 정보와 씰을 뜯는 방향이 표시되어 있다.
저 방향대로 씰을 뜯으면 상자가 개봉된다.
드디어 개봉한 상자. 그림과 똑같이 생겼다.
상자에는 맥 미니 본체와 전원선만 들어있었다.
맥 미니 포트
맥 미니는 컴퓨터의 본체 역할이기 때문에 여러 포트가 앞 뒷면에 나뉘어 배치되어 있다.
앞면에는 C 타입 두 개와 오디오 포트가 있다.
키보드나 마우스, 헤드셋을 연결하는 용도겠지?
뒷면에는 전원과 랜선, HDMI, C 타입 포트 두 개와 썬더볼트 하나가 있다.
아래에는 포트는 아니지만 전원 버튼이 있다.
전원을 연결하면 커지는 게 아니라 버튼을 눌러야 켜지는가보다.
연결
초기 설정을 위해 전원과 랜선, 모니터에 연결 되어있는 C 타입 케이블을 꽂아주었다.
키보드와 마우스는 모니터를 통해 연결되어 있다.
역시 전원 버튼을 눌러야 하는지 케이블을 꽂는 것만으로는 반응이 없었다.
아랫면에 있는 전원 버튼을 꾹 눌러주니 불이 들어오면서 맥 특유의 부팅 알림 소리가 났다.
맥 미니에도 스피커가 있다는 사실을 처음 알았다.
어려움 없이 성공적으로 부팅할 수 있었다.
데스크 세팅
지금 내 책상은 다음과 같은 모습이다.
책상 위는 다음과 같이 구성되어 있다.
픽셀 태블릿
모니터 / 웹캠 / 키보드 / 마우스
맥북 미니
웹캠, 키보드, 마우스는 모니터에 연결 되어 있고, 모니터 아래에 KVM 스위치를 통해 윈도우 데스크탑과 업무용 맥북간 전환한다.
이제 맥북 미니가 생겼으니 전환할게 하나 더 늘은 셈인데, 내가 가진 KVM 스위치는 2개짜리이다.
선도 깔끔하게 유지할 겸 맥 미니는 직접 연결하지 않고 크롬 원격 데스크톱 (Chrome Remote Desktop, CRD)로 연결했다.
이제 세 개 장치 (윈도우 PC, 회사 맥북, 맥미니) 간 빠르게 전환하며 작업할 수 있는 환경이 되었으니 내가 이를 잘 활용할 수 있기를 기대해본다.
02024. 12. 22.

일상
티스토리를 떠난 이유
2024년 11월 13일, 6개월 간 28개의 포스트를 올렸던 티스토리를 떠났다.
처음 티스토리를 시작한 건 2024년 5월이었다.
여러 블로그 서비스들 중 티스토리를 선택한 것은 스킨의 자유도에 있었다.
티스토리는 커스텀 스킨 템플릿을 지원해서 내가 직접 html/css를 이용해 스킨을 꾸밀 수 있게 해주었다.
이에 홈페이지와 게시글 페이지 등을 내가 원하는 스타일대로 꾸밀 수 있었다.
그러나 단점이 너무나 명확해 시간이 지날수록 이러한 장점을 유지하기가 힘들었다.
내가 꼽는 티스토리의 대표적인 단점은 다음과 같다.
커스텀 스킨을 위한 코드 유지가 어려움
내가 원하는 서비스 지원 불가
로봇 댓글 도배
아예 블로그 서비스를 직접 개발하는 것이 낫겠다 싶은 만큼 체감됐던 티스토리의 문제점을 하나씩 짚어보자.
티스토리의 문제점
1. 커스텀 스킨을 위한 코드 유지가 어려움
티스토리는 커스텀 스킨을 제공하지만, 모든 페이지에 대한 스킨 내용을 한 파일에 몰아넣어야 한다.
홈페이지, 게시글 페이지, 게시글 목록 등 여러 페이지에 적용하기 위한 하나의 html 파일과 하나의 css 파일로 구성돼있다.
이렇기 때문에 재사용성이 매우 떨어지는 것은 물론, 작은 것 하나를 바꾸려고 해도 1000줄에 달하는 코드에서 매번 스크롤을 내리며 코드의 위치를 찾아야 했다.
js 처럼 동적인 것을 넣으려면 상황은 더욱 심각해졌다.
html에 넣자니 코드 작성부터 힘들다.
티스토리에서 지원하는 정적 파일 업로드를 이용하기엔 조금씩 수정할 때마다 새로 업로드를 하면서 외부에서 버전 관리를 해주어야 했다.
결국 파일이 커질수록 수정이 점점 더 어려워졌고, 어느 순간부터 사소한 변경마저도 너무 큰 일이 되면서 더 이상 스킨을 업데이트 하지 않게 되었다.
2. 내가 원하는 서비스 지원 불가
프로그래밍 관련 포스트가 많은 개발 블로그 특성 상, 시리즈로 포스트를 연재할 일이 많다.
그래서 카테고리 안에 시리즈로 여러 게시글을 묶을 수 있는 기능이 있었으면 했다.
이 외에도 티스토리에서 정해 놓은 시스템 기반의 블로그이기 때문에 자유도가 많이 떨어졌다.
3. 로봇 댓글 도배
이 댓글들이 티스토리에 가장 많이 정을 떨어뜨리게 했다.
티스토리에는 일정 주기 이상으로 포스트를 하면 광고를 개제할 수 있다.
이렇게 광고를 개제한 수익화 블로그를 운영하는 사람들이 다른 블로그에 들어가 댓글을 남기고, 자신의 블로그 유입을 늘리기 위한 댓글 로봇을 운영하는 것 같다.
달리는 댓글들이 전부 "내 블로그에도 방문했으니 자신의 블로그에도 방문해달라"라는 내용이었다.
이 의미도 없는 댓글들 중엔 심지어 광고를 클릭했으니 자기 광고도 클릭해달라라는 댓글들도 많았다.
내 블로그에는 광고가 없는데 말이다. 양심도 없지...
새로운 블로그로 이전
이런 이유들로 티스토리를 버리고 직접 블로그를 만들기로 했다.
새 블로그는 Next.js와 파이어베이스로 만들고, Vercel에서 호스팅 중이다.
배포하고 이전한지 한 달 정도가 지났는데, 생각보다 만족도가 높다.
직접 OpenGraph 세팅과 SEO용 메타 데이터 설정을 해서 그런지 구글 검색 결과에 블로그가 노출되어 있는 것을 보면 뿌듯하기도 하다.
아직 댓글이나 좋아요 등 티스토리 블로그 때에 비하면 없는 기능들도 있지만, 직접 만드는 블로그이니 걱정은 없다.
하나씩 만들다보면 언젠간 다 만들어져 있겠지.
02024. 12. 22.

프로그래밍
개발자와 글쓰기
프로그래밍과 글쓰기는 언뜻 비슷하면서도 다른 것 같이 느껴진다.
코드를 쓰는 것과 글을 쓰는 것.
둘 다 무언가를 쓰는 것이기 때문에 비슷한가 하면서도 막상 쓰는 것이 다르기 때문에 별개로 접근해야 하지 않나 싶기도 하다.
그러나 그 본질을 들여다보면 두 행위는 같고, 심지어 개발자라면 글쓰기 연습을 필수적으로 해야 한다고 생각한다.
물론 개발자가 깔끔하고 명확한 문서를 작성하기 위해서는 글쓰기 능력이 필요할 것이다.
하지만 그것보다 더욱 본질적인 세 가지 이유가 있다.
읽는 사람을 생각한다코드와 글은 모두 읽는 사람을 고려해서 작성해야 한다.
단순히 원하는 기능이 작동하기 위해 코드를 쓰거나, 말하고 싶은 내용을 담기만 하는 글쓰기는 이해하기 어렵다.
가독성을 따지기 위해 읽는 사람 입장에서 생각하는 연습을 한다면 좋은 코드나 글을 작성하는 것이 훨씬 쉬워진다.
논리적 근거를 생각한다글을 쓸 때 무언가 주장을 하기 위해서는 근거가 필요하다.
프로그래밍도 어떤 코드를 작성할 때 근거가 필요한다.
한 가지를 구현하더라도, 여러 방법을 비교해보고 장단점을 파악하여 프로젝트 상황에 가장 적합한 것을 논리적 근거와 함께 선택해야 한다.
비판적 사고를 한다."인용"은 글을 쓸 때 이름 있는 사람의 말을 빌려 주장을 뒷받침할 수 있다.
그러나 그 인용이 내가 쓰고 하는 글의 상황에 맞는지를 잘 따져봐야 한다.
프로그래밍도 마찬가지로 공신력 있는 문서의 주장을 근거로 삼기 위해서는 해당 문서의 상황과 현재 프로젝트의 상황이 얼마나 일치하는지를 생각해 봐야 한다.
상황이 다르다면, 해당 문서의 주장은 그저 참고용일 뿐이다.
나중에 이와 관련해서 요즘IT에 글을 써봐야겠다.
https://yozm.wishket.com/magazine/@spaceship00/
02024. 12. 15.

일상
오징어 게임2 구글 이스터에그 - 무궁화 꽃이 피었습니다 미니 게임
회사에서 20% 프로젝트로 진행하던 오징어 게임2 이스터에그가 이번 주 출시되었다.
[오징어 게임]이나 [오징어 게임2]를 검색하면 다음과 같이 오징어 게임 초대장이 표시된다.
이 초대장을 클릭하면 영희와 6명의 참가자들이 나타나고 무궁화 꽃이 피었습니다 미니 게임을 할 수 있다.
O를 누르면 참가자들이 영희를 향해 이동하고,
X를 누르면 그 자리에 멈춘다.
영희가 참가자들을 보고 있는 상태에서 움직이면 가장 앞에 있는 참가자가 탈락한다.
한 명이라도 통과하면 게임은 승리하지만, 모든 참가자를 통과시킬 수 있다면 더욱 좋은 일이 일어날지도..?
구글 오징어 게임 이스터에그: https://g.co/kgs/x7eqEpJ
02024. 12. 14.

일상
제미나이 이미지 생성 - 투슬리스 그리기
점심 시간에 회사 사람들과 이야기하다 제미나이의 이미지 생성에 대한 이야기가 나왔다.
제미나이의 이미지 생성은 생각보다 강력하다.
올해 8월 말, 구글의 이미지 생성 AI인 Imagen3가 제미나이에 적용되면서 제미나이를 이용해 Imagen3로 이미지를 생성할 수 있게 되었다.
당시에 테스트로 드래곤 길들이기의 투슬리스 이미지를 생성해 봤는데 애니메이션과 구분되지 않을 정도로 똑같은 모습을 구현했었다.
바로 회사 사람들과 다시 투슬리스 이미지를 생성해 보았다.
" 드래곤 길들이기의 투슬리스 그려줘
너무 잘 그려줬다.
독특한 장면을 연출하고 싶어 다음과 같은 프롬프트를 입력했다.
" 드래곤 길들이기의 투슬리스가 아이스크림을 먹는 모습을 그려줘
이 모습도 귀엽지만 아이스크림을 먹고 있는 모습을 보고 싶었다.
" 혓바닥이 나와있게 그려줘
혀는 내밀었지만 아이스크림을 핥고 있진 않다.
" 드래곤 길들이기의 투슬리스가 아이스크림을 들고 핥아 먹는 모습을 그려줘
굳이 혀를 대지 않아도 핥아 먹는다고 생각하나보다.
조금 더 자세한 프롬프트를 넣어 보았다.
" 드래곤 길들이기의 투슬리스가 아이스크림을 들고 혀로 핥아 먹는 모습을 그려줘. 혀가 아이스크림에 닿아 있어야 해
드디어 원하는 결과가 나왔다.
아이스크림을 들고 핥아 먹는 투슬리스이다.
만족스러운 결과였다.
이후에 색다른 모습을 보고 싶어 다음과 같은 프롬프트를 넣어 보았다.
" 투슬리스가 한복 입은거 그려줘
그리고 그 결과는 놀라웠다.
투슬리스가 너무 자연스럽게 한복을 입고 있었다.
제미나이의 이미지 생성... 강력하다.
전체 제미나이 프롬프트 링크: https://g.co/gemini/share/daef155056dd
02024. 12. 11.

일상 > 뉴욕 출장기
5일차 - 브런치, 허드슨 오피스, Sappe (2024년 9월 4일)
출장을 와서 가장 좋은 점 중 하나는 한국 팀이 하고 있지 않은 프로젝트에 대한 이야기를 듣기 쉽다는 것이다.
아무래도 한국에 있으면 우리가 하고 있는 프로젝트에 대한 이야기 위주로 대화가 흘러간다.
뉴욕에 오고 옆 팀 사람들이랑 이야기를 하다 보면 우리가 하고 있는 프로젝트가 저런 방식으로 발전될 수도 있다는 생각이 들며 시야가 넓어지는 느낌이 든다.
시야가 좁으면 발휘할 수 있는 창의력에도 한계가 생긴다.
이번 출장은 다양한 의견과 프로젝트를 보면서 내가 하고 있는 프로젝트가 어떻게 발전될 수 있을지, 어떤 게 부족한지에 대한 실마리를 잡는 좋은 계기가 된 것 같다.
오전 8시 30분 아침
같이 출장 온 일행과 함께 오피스 가는 길에 있는 브런치 가게를 방문했다.
La Bergamote라는 곳이다.
나는 Eggs Baltic을 주문했다. 에그 베네딕트랑 비슷한데, 구성이 조금 다르다고 한다.
음식이 준비되기 전에 커피를 먼저 주었다.
따뜻한 디카페인 아메리카노를 주문했다.
주문한 에그 볼틱이다.
색이랑 모양도 좋고, 맛도 맛있었다.
나는 반숙보다 조금 덜 익은, 개인적으로 안숙이라고 부르는 상태를 좋아하는데, 딱 그 정도 익힘 상태였다.
다른 분들에게 나온 메뉴들도 보면 전부 화려하다.
아마 왼쪽이 팬케익이고 오른쪽이 프렌치토스트인데, 내가 생각한 비주얼과 달라도 너무 달랐다.
내 머릿속의 팬케익은 얇은 팬케익에 시럽 뿌려져 있고 위에 버터 조각이나 올라가 있는 모습이었고, 프렌치토스트는 계란물 발라 구운 식빵일 뿐이었는데,
위에 올라간 과일과 베리가 색감을 더해줬기 때문일까, 전부 너무 맛있어 보였다.
오후 1시 허드슨 스퀘어 오피스에서 점심
뉴욕에는 전 날 방문한 4개 오피스 외에도 서쪽에 하나의 오피스가 더 있다.
허드슨 스퀘어에 있는 오피스인데, 지은 지 얼마 안 된 오피스라고 한다.
그리고 현지 팀원분이 여기에서는 다른 오피스 내 식당과는 달리 서빙까지 해주는 식당이 있다고 얘기해 주었다.
다만 이 식당은 예약이 필요한데, 자기가 마침 예약해 둔 것이 있어서 같이 가자고 해주었다.
식당 입구에서 예약을 확인하고 입장한다.
지금 예약 확인 중인 분이 뉴욕에 있는 팀원분이다.
예약이 확인되면 빈자리로 안내해 준다.
회사 식당에서 이런 시스템은 처음이긴 하다.
팀원분 말로는 아마 아래쪽에 월 스트리트가 있어서 그쪽 클라이언트와 미팅 용으로 만든 게 아닐까 한다고 한다.
확실히 지인 게스트가 아니면 정장을 입고 있는 사람들이 많은 것 같았다.
안내받아 앉은자리에 이 날의 메뉴가 출력되어 있었다.
신기하긴 했지만... 하나 빼고는 다 비건이거나 베지테리언이다.
어려운 영어의 이름을 가진 빵이다.
소스가 맛있었다.
뭔지 모르겠는 빨간 음료도 줬다.
알코올은 당연히 아니고, 주스도 아닌데, 무슨 베리로 만든 음료인 것 같다.
그냥 채소다.
나머지 세 개도 그다지 내 취향은 아니었다.
제일 왼쪽은 가지와 버섯이 있었고, 가운데는 익힌 당근이었다.
그나마 제일 오른쪽에 있는 생선이 제일 나았는데, 이마저도 너무 짰다.
원래 짠 거에 대해서는 관대한 편인데 상당히 짰다.
결국 여기는 신선함으로 오는 것이고 음식 보고 오는 건 아닌 걸로...
오후 6시 팀 저녁
뉴욕에 있는 팀원들과 팀 회식을 나갔다.
오피스 근처에 있는 Sappe라는 곳인데, 태국 음식점이다.
한국에서 출장 온 3명과, 뉴욕 현지에 있는 6명이 더해 총 9명이서 갔다.
온라인으로 메뉴를 보고 주문할 수 있었다.
https://www.sappenyc.com/
칵테일과 음식을 하나씩 주문하기로 했다.
나는 칵테일로 Boonrod라는 칵테일을 주문했다.
먹을 만 하긴 했지만 딱히 취향은 아니었다.
코코넛 시럽이 들어가서 그런지 감기약 맛이 나는 것 같았다.
음식으로는 Mama E-La라는 소고시 계란 국수 볶음을 주문했다.
다른 분들이 주문한 음식은 좀 많이 매운 경우가 있었는데, 이건 맵지 않고 달고 맛있었다.
팀 저녁 이후에는 각자 퇴근했다.
적당히 술을 마셔서 그런지 하루가 기분 좋게 마무리되었다.
02024. 10. 11.

일상 > 뉴욕 출장기
4일차 - 오피스, 브루클린 배드민턴 센터 (2024년 9월 3일)
미국의 휴일이 끝나고 오피스가 정상 운영되는 첫 날이다.
그동안 열심히 돌아다녔으니 이제부터는 본격적으로 일을 하면서 퇴근 후 남는 시간에 남은 관광을 조금씩 했다.
오전 7시 30분 기상
이 날은 하늘에 구름이 없었다.
며칠 새에 가을 하늘이 되어버렸다.
오전 8시 30분 오피스 아침
오피스에서 아침을 먹었다.
서치는 전 포스트에서 가본 오피스 중 9번가 오피스에 있다.
https://hyuni.dev/posts/iGsBxcX6PtrYUDhd8t0k
이 건물의 식당 중 한 곳에서 같이 출장 간 팀원분들과 함께 아침을 먹기로 했다.
여러 개의 코너가 있었다.
계란, 베이컨, 빵, 과일, 스무디 등등이 있었다.
다른 분꺼랑 비교했을 때 너무 채소가 없나 싶기도 하고...
오전 9시 10분 업무
아침 식사 후 일을 하러 이동했다.
우리 팀은 4층에 있었는데, 전날에는 위층부터 내려오다 첼시 오피스로 이동해서 처음 가보는 층이었다.
의도치 않게 효율적인 관광이 되어버렸다.
4층에는 커피와 스무디 코너가 있었다.
스무디는 원하는 재료를 선택하면 그 자리에서 갈아주는 시스템이었다.
가장 무난해보이는 재료들인 바나나와 망고를 선택하고, 아몬드 밀크를 베이스로 만들어 달라고 했다.
나중에 현지 분들한테 물어보니 깔끔하게 잘 만들었다고 했다.
바나나를 넣으면 다 맛있어진다고 한다.
4층에는 레고 라운지 공간이 있었는데, 한쪽 벽면에 레고 조립품이 깔려있었다.
라운지 가운데 있는 책상 중간에는 레고가 들어있는 홈이 파여 있어 책상에 앉아서 조립할 수 있게 해두었다.
위층으로 통하는 사다리도 뚫려있었는데, 이 날은 사람이 많아 차마 시도해보지는 못했다.
전날 4층을 왔었다면 무조건 올라가봤을 것이다.
오후 1시 30분 점심
업무를 하다가 점심을 먹으러 갔다.
이 건물에도 식당이 여러 군데 있는데, 그 중에 나는 햄버거를 주는 곳으로 갔다.
원하는 빵 종류랑 패티를 고르면 그걸 준비해주고, 거기에 기타 채소나 소스를 추가해 먹는다.
햄버거를 만들고 계란과 함께 김치도 있길래 받았다.
오후 5시 브루클린 배드민턴 센터
그래도 명색이 구글 코리아 배드민턴장인데 뉴욕 오피스의 배드민턴을 경험해보아야 했다.
이미 출국 전 뉴욕 클럽장과 이야기해 운동할 수 있는지를 물어봐놓은 상태였다.
원래라면 오피스 근처에서 운동을 한다고 하는데, 그곳이 공사중이라 브루클린까지 가야 하고, 그래서 사람이 많이 안모일 수도 있다고 했다.
그래도 그 분도 어지간히 운동을 하고 싶었는지 어떻게 어떻게 사람을 모아서 6명이서 배드민턴 모임이 성사되었다.
5시부터 6시 반까지 한 시간 반동안 한 코트를 대관했다.
나는 그 날 7시 30분에 다시 오피스로 돌아가 회의를 해야 했기 때문에 딱 적당한 시간이었다.
브루클린 배드민턴 센터는 꽤 규모가 있었는데, 총 7면의 코트가 있었고, 천장도 높았다.
탈의실도 있었다.
샤워 시설이나 음료를 파는 곳은 없는 듯 했다.
문제는 출근할 때 배드민턴복을 안챙겨왔다.
위에는 입고 있었는데, 운동 바지가 없었다.
체육관에서 팔지도 않아서 긴 바지를 걷어 붙이고 쳐야 했다.
오후 7시 45분 오피스
원래라면 6시 반까지 운동을 마무리하고 7시 30분까지 오피스에 돌아와서 회의에 들어갔어야 했는데...
6시 반에 다음 팀이 안와서 시간을 확인 못하고 배드민턴장에서 늦게 출발하게 되었다.
오피스 건물에 가서도 저녁이라 정문이 닫혀있어 입구를 못찾아 건물을 세 바퀴를 돌았다.
결국 회의에 늦어버렸다ㅠ
분명 전 날 들어왔던 입구였는데, 너무 많은 곳을 돌아다녀서 인지를 못한 것 같았다.
이렇게 뭔가 우당탕한 공식적 첫 날이 지나갔다.
02024. 10. 10.

일상 > 뉴욕 출장기
3일차 - 구글 오피스 투어 (2024년 9월 2일) - 스압 주의
관광을 위한 주말이 지나 월요일이 되었다.
문제는 한국의 월요일은 평일이었지만, 이 날 미국은 노동절로 인한 휴일이었다는 점이다.
오피스를 가도 사람이 없고, 밥도 안 줘서 같이 출장 간 다른 분들은 오피스에 굳이 가지 않는다고 하셨다.
하지만 뉴욕 오피스가 처음인 나에게는 다른 사람들 눈치 안 보고 오피스를 마음껏 돌아다니며 구경할 수 있는 날이었다.
워낙 뉴욕 오피스가 좋다는 이야기를 많이 듣고, 오피스들이 일렬로 쭉 붙어 있어서 둘러보고 일을 하기로 했다.
위 사진의 가장 왼쪽에 있는 오피스는 있는지 몰랐는데, 오피스를 둘러보면서 알게 됐다.
오전 10시 30분 출발
호텔에서 조식을 먹고 출근 준비를 해서 10시쯤 호텔을 나섰다.
오피스 가는 길
첫 목적지는 내가 속한 서치 팀의 주요 업무 공간인 Google NYC - 9th Avenue, 9번가 오피스이다.
뉴욕 맨해튼은 격자 구조로 도로가 나있어서 Street와 Avenue의 번호를 이용해 주소를 쉽게 알 수 있다.
호텔이 오피스와 멀지 않아 도보로 15분 정도 걸린다.
역시나 맨해튼 거리의 대명사답게 그리드의 어느 경로로 이동해도 같은 시간이 걸린다.
10시 50분 9번가 오피스
오피스에 도착했다.
휴일이라 정문이 닫혀있어서 어디인지도 모를 쪽문으로 들어갔다.
총 16개 층으로 구성되어 있었고, 16층 테라스는 휴일이라 닫은 것 같아 14층부터 보면서 내려오기로 했다.
층 수가 많은 만큼 식당도 많았는데, 여기 있는 식당들은 평일에 일하면서 방문하니 이번 포스트에서는 생략하겠다. (식당 외에 쓸게 너무 많다)
MK (마이크로 키친)
구글에는 마이크로 키친이라고 하는 간식이나 음료들을 가져다 먹을 수 있는 공간이 있다.
오피스를 들르고 가장 처음 한 것은 MK에 어떤 간식이 있는가를 확인하는 것이었다.
이렇게 통에 작게 포장된 여러 군것질할 것들이 들어있었다.
바로 피넛 M&M을 꺼내 먹었다.
미국에서 나는 여러 과자들이 있다.
먹어보지는 않았다.
체다 버니라는데 맛있어보이기는 하지만 상당히 살찔 것 같은 이름과 비주얼이다.
사진에 보니 비스킷 하나에 130kcal 라는 듯..?
놀랍게도 김이 있었다.
이름도 gimme이었다.
궁금하긴 했지만 별로 좋아하지 않는 아보카도가 있어서 패스했다.
간식들 중에 이 두 가지를 시도했다.
감자칩은 무난하고 맛있었지만, 프로틴 바는... 한 입 먹고 버렸다.
땅콩버터와 초콜릿 맛이 나기는 했지만 그보다 훨씬 텁텁하고 사료 같은 느낌이 강해서 먹을 수가 없었다.
오피스에는 여러 개의 MK가 있다.
MK 간 구비해놓는 품목은 거의 같은데, 꾸며 놓은 방식은 조금씩 다르다.
이 MK는 과일을 메인으로 진열해 놓았다.
여러 종류의 음료수도 있다.
레모네이드를 좋아해서 이번 출장 내내 꽤 마셨다.
다른 음료들은 시도해봤지만 영 별로였다.
티 종류가 많았는데, 맛이 없는 건 아니지만 너무 맛이 약해서 깔끔하다고 하기에도 애매하고 맛있다고 하기에도 애매한 맛.
오피스 둘러보기
뉴욕 오피스에서는 안마 의자가 이렇게 밖에 나와있었다.
서울 오피스의 안마 의자는 어두운 공간에 좀 더 프라이빗하게 있는데, 여기는 복도 중간에 있어 나 같은 사람들은 쓰기 힘들 듯...
대신에 밖에 뷰를 보면서 할 수 있다는 것은 좋은 점 같다.
MK 근처에 커다란 곰 인형이 한 자리를 차지하고 있었다.
오피스가 매우 커 계단이 많았는데, 그 중 하나에 이렇게 인테리어가 돼있었다.
밖을 보면서 커피를 마시거나 수다를 떨 수 있는 공간이 꽤 많았다.
층이 높고 뷰가 좋아 많이 찾을 것 같다.
한쪽 벽면에 식물들을 놓은 복도이다.
가까이서 보니 화분에 심긴 식물들을 배치해 놓은 것이었다.
관리가 힘들 것 같은데 보기에는 좋아 보였다.
계단과 사다리
오피스 내에서 다른 층으로 이동할 수 있는 계단들이 있다.
물론 한국에서도 화재 대피를 위한 계단이 있어 계단으로 이동할 수 있지만, 그건 오피스 밖으로 나가서 계단을 타는 것이다.
여기서 살펴보는 건 건물 설계 자체부터 여러 층을 통과하는 계단을 만들어 놓은 경우들이다.
이 계단은 내 기억상 8층, 9층, 10층을 통과했던 것 같다.
9층과 10층 사이에는 해리포터의 9와 3/4 승강장을 패러디한 9와 3/4층의 작은 공간이 있었다.
오피스를 돌아다니다보면 이렇게 중간에 다른 층으로 가는 길이 나온다.
워낙 층이 넓어서 구석 구석 계단을 놔두는 것 같다.
사진 오른쪽을 보면 킥보드가 있는데, 넓은 오피스를 빠르게 돌아다니기 위해 층 별로 킥보드가 구비되어 있어 실내에서 타고 다닐 수 있다.
이 계단은 나선형 계단이었다.
야외 테라스
대부분의 테라스는 닫혀 있었지만, 열리는 테라스를 발견해서 나갔다.
하늘도 맑고 그늘도 져 밖에 있기 딱 좋았다.
한산하고 평화로운 분위기가 좋다.
서울 오피스에는 야외 테라스가 없어서 이렇게 실외에서 뉴욕을 내려다볼 수 있는 공간이 있다는 게 부러웠다.
오후 1시 30분 첼시 오피스
9번가 오피스는 너무 커서 모든 층을 다 돌아보다가는 끝이 없을 것 같았다.
위에서 몇 개 층만 봤는데도 어느덧 2시간 반이 흘러버려서 얼른 다른 오피스로 이동했다.
다음으로 간 오피스는 바로 옆 건물인 첼시 오피스이다.
첼시 오피스는 꽤 유명한 관광지인 첼시 마켓이 있는 건물 위에 있다.
건물 층수가 높지 않아 금방 둘러볼 수 있을 것 같았다.
구석에 아늑해보이는 방이 있었다.
화면이 좀 작긴 한데 다 같이 뭔가 틀어놓고 보면 좋을 것 같기도?
오피스 식당
첼시 오피스에도 식당이 있었다.
건물 외관도 그렇고, 붉은 벽돌로 만든 벽이 메인 컨셉인 것 같다.
식당이 총 3층까지 있었는데, 위에는 사람이 일하고 있는 것 같아 더 이상 올라가지는 않았다.
한국에서 뉴욕 오피스에 대한 이야기를 들었을 때 오피스가 연결되어 있다고 했다.
건물에 대한 감이 없는 상태에서 들어서 어떻게 연결되어 있다는 건지 몰랐는데, 첼시 오피스의 안내도에 나와 있었다.
첼시 오피스의 4층이 옆 건물과 연결되어 있었다.
이걸 발견하고 목적지는 저 통로가 됐다.
(지금 발견했는데, 아래에 피어 오피스와 4개 건물 아래에 있는 조그마한 오피스가 그려져 있다. 피어 오피스는 나중에 발견해서 가봤지만 450W15 오피스는 못 가봤다)
라운지로 가는 길에 발견한 포토 스팟
통로를 찾으러 가는 길에 표지판과 수상하게 생긴 공간을 발견했다.
당시에는, 그리고 지금 이 사진을 올리면서 이게 오피스에서 어디쯤인지 찾아볼 때만 해도 이 공간은 그저 사진 찍기 좋았던 공간일 뿐이었다.
그런데 지금 여기를 찾아보니... 가보지 못했던 다른 오피스와 연결해 주는 통로였다.
심지어 Oreo Way Skybridge라는 이름도 가지고 있는 나름 이름 있는 다리였다.
이 사실을 알고 나니 뭔가 더욱 당시 경험이 특별하게 느껴진다.
밖에서 사람들이 저 다리를 찍을 때 나는 저 안에 있었다니...!
좌우에 이 다리가 잇는 두 건물이 보이고, 멀리에 하이라인으로 추정되는 다리에 사람들이 지나다니는 것이 보인다.
저기에 나랑 마주 보고 서로 사진을 찍은 사람이 있을 수도 있지 않을까?
의자와 휴대폰을 옮겨가며 사진을 여러 장 찍었다.
평일에 사람들 있을 때는 상상도 못 할 일이지만 지금은 오피스에 나 밖에 없다.
구글 오피스에는 잘 꾸며져 있는 곳이 많아 휴일에 오피스를 방문할 맛이 난다.
뭔가 평소에는 북적이는 관광 스팟에 나 혼자 있는 느낌이랄까.
라운지
첼시 오피스에는 큰 라운지도 있었다.
햇빛도 잘 들고 인테리어도 좋아 분위기가 있었다.
라운지 한쪽에 있는 식물들로 둘러싸인 바 테이블이다.
오피스 인테리어는 누가 하는 걸까. 편안한 느낌이 들어 좋다.
테이블 중간에 놓인 핫 소스가 사람들이 여기서 식사를 많이 한다는 것을 알려준다.
도서관 같은 느낌이 나서 뉴욕 공립 도서관에 못 간 걸 위안 삼을 겸 설정샷을 찍었다.
다리도 아파서 여기서 잠시 앉아서 메일 온 것들 확인 정도만 하며 잠시 쉬었다.
오후 2시 5분 첼시 오피스 -> 8510 오피스
첼시 오피스에 들어간 지 30분이 지나고, 8510 오피스로 향하는 다리를 발견할 수 있었다.
이 다리는 오레오 다리처럼 예쁘지는 않았지만 그래도 나름 뭔가를 갖다 놓기는 했다.
라운지가 있어서 업무 중간에 커피를 들고 와 이야기를 할 수도 있고, 밖을 보며 업무를 할 수도 있다.
다리에 돈비이블 벨트를 찬 곰이 있었다.
오후 2시 10분 8510 오피스
8510 오피스에 가자마자 나온 것은 하이 라인 카페였다.
하이 라인은 뉴욕의 관광 명소 중 하나인데, 오피스와 연결되어 있다는 이야기를 들었다.
나는 가보지 않았지만 아마 8510 오피스 건물이 연결되어 있어서 이름을 따온 게 아닐까 한다.
나는 휴일에 가서 바리스타가 없었지만, 평소에는 여기서 커피를 받아갈 수 있다.
하이 라인 카페에서는 식사로 스시가 나오는 코너가 있다. (들리는 소문으로는 그렇게 맛있지는 않다고 한다)
확실히 9번가 오피스에 있을 때보다 강가 쪽으로 나오다 보니 풍경이 많이 좋아졌다.
위 사진에서 강가에 보이는 공원이 Little Island라고 불리는 뉴욕의 관광 명소이다.
하이 라인 카페를 지나 오피스 안쪽으로 조금 더 들어오자 리셉션 공간이 나타났다.
여기서 소름 돋는 경험을 했다.
당시에는 너무 깜짝 놀라 소리 지를 뻔했다. 아래 영상을 보면 그 이유를 알 수 있다. (깜놀 아님)
https://www.youtube.com/watch?v=h2Pv-W4BzV8
영상에 나오지만, 아무 생각 없이 복도를 지나가고 있는데 옆에서 사사사삭 하는 소리가 들렸다.
대수롭지 않게 지나가려 하는데 그 소리가 나를 따라오는 것이다..!
옆을 봤더니 웬 사람 형상이 있어서 너무 놀라버렸다.
이 영상은 한 번 놀란 후 재연한 거라 침착하다.
특이한 컨셉의 방이 있었다.
자연이 컨셉이었는데, 여기서 힐링하라는 용도인 것 같다.
다리가 아팠어서 들어가서 조금 앉아있었다.
식물들은 다 진짜로 관리되고 있는 것 같았고, 스피커에서 새소리가 났다.
새소리는 너무 반복적이라 오래 있긴 힘들었다.
오후 2시 40분 점심 포장
여기까지 둘러본 후 점심을 먹으러 갔다.
나는 내가 오피스를 다 돌아본 줄 알았다.
그래서 이게 마지막 오피스라는 생각으로 주린 배는 움켜잡고 아픈 다리는 이끌면서 힘겹게 돌아다녔다.
그리고 마지막(이라고 생각한) 오피스를 다 돌아본 후에야 늦게 점심을 먹으러 간 것이다.
점심은 첼시 마켓으로 갔다.
여기서 점심을 포장해서 오피스에 가서 먹을 생각이었다.
출장을 같이 간 분들 중 한 분의 와이프분이 첼시 마켓에서 해산물, 특히 랍스터와 굴이 괜찮다고 하셔서 랍스터를 시도해 보기로 했다.
이왕 왔으니 랍스터 한 마리를 통째로 찐 것을 주문했다.
랍스터 포장된 것을 받고 다시 8510 오피스로 돌아갔다.
문제는 여기서 발생했다.
점심을 먹기 위해 적당히 강가 뷰이면서 음료도 구비되어 있는 MK를 찾다가 옆 건물에 구글이 적혀 있는 것을 발견한 것이다.
옆 건물은 강으로 삐져나와있는 건물이었기 때문에 무조건 강가 뷰인 MK가 있을 것이 자명했다.
3킬로의 맥북을 지고, 랍스터 포장을 들고 정말 너무 배고프고 힘들었지만 언제 또 뉴욕을 와보겠냐는 마음으로 버텼다.
오후 3시 15분 피어 오피스
대로를 하나 지나면 바로 오피스라 거리는 멀지 않았다.
맨해튼은 피어가 굉장히 많다.
그중 하나에 구글 오피스가 있다는 사실이 새삼 신기했다.
건물 밖에 구글이라고 쓰여있고, 직원들은 여기로 출입했다.
내가 8510 오피스에서 발견한 구글 문구도 이 문이었다.
오피스 입장
입구 안쪽에는 배지를 태그하고 들어갈 수 있는 계단과 에스컬레이터가 있었다.
이 오피스는 상당히 넒직하게 구성되어 있었다.
얼른 점심 먹을 곳을 물색해야 했지만 그래도 둘러보는 걸 참을 수는 없었다.
외부 게스트들을 위한 라운지 공간이 있었다.
클라우드 마케팅 팀에서 클라이언트 초청했을 때 사용하는 공간인 것 같았다.
이런 식으로 컨퍼런스 홀도 마련되어 있었다.
식당과 연결된 곳에 테라스가 있었는데, 콘으로 막혀있어 들어가 보지는 못했다.
치우고 들어갈까 잠시 고민을 해보긴 했는데 차마 실행하지는 못하겠더라.
드디어 점심
결국 주변을 도는 시큐리티 분한테 물어봐 나름 뷰가 괜찮은 MK를 찾았다.
창과는 거리가 있어 뷰가 살짝 아쉽긴 했지만 어차피 뷰 많이 봤고 이제는 진짜 먹을 때였다.
이때가 3시 30분이다.
랍스터는 손질이 잘 돼있어 먹기 편했고 맛있었다.
전에 먹었던 랍스터는 사람들이 내장이 맛있다고 하는 말을 잘 이해 못 했는데, 이건 맛있었다.
살도 많았다.
버터 소스를 같이 줬는데, 나는 그냥 먹는 게 더 맛있었다.
업무 시작
먹으면서 좀 쉰 후에, 이제는 일할 장소를 찾아보았다. 조건은 밥 먹을 때와 마찬가지였다:
MK가 근처에 있어야 함
강 뷰가 보여야 함
그러다 오피스 안쪽에서 완전 강가로 창이 나있는 공간을 발견했다.
뉴저지까지 쭉 보이는 강 뷰였다.
사람들이 보트를 타고 수상 스포츠를 즐기는 모습을 평화롭게 감상할 수 있었다.
MK도 멀지 않아 완벽한 스팟이었다.
여기에 노트북을 펼치고, 충전기를 꽂고 일을 시작했다.
오후 5시 30분 - 다시 8510 오피스로
피어 오피스에서 어느 정도 일을 하다 보니 밖에 뷰가 좀 심심해지기 시작했다.
강 뷰가 좋지만 층이 낮고 사람이 별로 없어 평화에서 오는 지루함이 느껴졌다.
8510 오피스의 고층으로 가서 업무를 이어가기로 했다.
피어 57을 둘러서 사람들이 조깅을 많이 했다.
나도 8510 오피스로 돌아가는 길에 그 길을 따라 둘러가 보았다.
전에 8510 오피스에 왔을 때는 첼시 오피스에서 넘어온 거라 저층부에 있었다.
고층에 오니 식당을 발견할 수 있었다.
여기서 작업을 하려고 하는 순간, 충전기를 피어 오피스에 두고 왔다는 것을 깨달았다.
바로 다시 가기는 힘들어서 일을 하다 중간에 가지러 갔다 왔다.
역시나 뷰는 좋았다.
고층 뷰이고, 강도 보이면서 차와 사람들도 잘 보이는 만족스러운 뷰였다.
여기도 MK가 근처라 편했다.
MK에 샌드 아트가 있었다.
해볼까 하다가 그냥 뒀다.
오후 7시 스타벅스 리저브
오피스 근처에 큰 스타벅스 리저브가 있었다.
여기서 기념으로 작은 컵을 샀다.
이 컵을 계산하러 갔는데, 직원이 컵을 떨어뜨려 산산조각을 냈다.
새 걸로 다시 계산해 줘서 나는 상관없었지만 괜히 마음이 안 좋았다.
저렇게 되면 월급에서 까이는 걸까?
오후 7시 30분 호텔 복귀
오피스 투어를 마치고 호텔로 돌아왔다.
오피스가 너무 크고 많아서 첫날 박물관을 돌아다닌 것 이상으로 힘들었던 것 같다.
실제로 이 날 걸은 걸음은 2만보로 출장 중 가장 많이 걸은 날이다.
사진에는 9월 3일로 나오지만 시차 때문이고, 뉴욕 시간으로는 9월 2일 걸은 걸음이다.
정말 힘들었지만, 뉴욕의 오피스를 어떤 방해도 없이 둘러볼 수 있었던 훌륭한 하루였다.
02024. 10. 09.

일상
1일차 - 센트럴 파크, 자연사 박물관 등 (2024년 8월 31일)
12시가 넘어 호텔 체크인 한 후 자고 일어난 실질적 뉴욕 첫날이 밝았다.
이 날은 토요일이어서 센트럴 파크 쪽을 돌아다녀볼 계획이었다.
오전 6시 기상
역시 정반대의 시차에 낯선 환경인 것이 시너지를 일으켜 늦게 잔 것이 무색하게 일찍 눈이 떠졌다.
그리고 어제보다 밝아진 뉴욕의 뷰가 반겼다.
호텔의 뷰에 감명받아 뷰만 몇 장을 찍었는지 모르겠다.
사진을 찍고, 오늘 계획을 세우고 하다보니 시간이 조금 더 지나 아침이 제대로 밝았다.
뷰가 너무 아까워 평소에 하지 않는 설정샷도 찍어보았다.
이제 휴대폰 배터리가 바닥나기 전에 얼른 충전용 어댑터를 사러 나가야 한다.
오전 7시 어댑터를 찾아서
아침 일찍 어댑터도 살 겸 뉴욕 거리도 둘러볼 겸 밖으로 나왔다.
나오면서 호텔 조식 운영 시간을 보았는데, 7시가 되기 직전이라 빨리 사 오면 되겠다 생각하고 조식은 먹지 않고 나갔다.
뉴욕 거리 둘러보기
당시에는 "와 건물들 예쁘다!" 하고 찍었는데 지금 보니 역시 거리가 더럽긴 하다..ㅋㅋㅋ
실제로 뉴욕 거리에서는 냄새가 많이 난다.
기본적으로 쓰레기 냄새가 베이스로 깔려 있고,
중간중간 오줌 냄새가 난다.
거기에 가끔 약물 냄새가 강력한 한 방을 날린다.
문제는 이 "중간중간"과 "가끔"의 빈도가 생각보다 자주 발생한다.
나는 이 냄새 때문에 첫날은 거의 밥을 넘기기 힘들었다.
이름만 들어본 Best Buy도 봤다. 오픈 전이라 들어가 보지는 못했는데 한국에선 볼 수 없는 픽셀 제품을 판매하고 있었다.
지하철도 보여 들어가 보았다. 사실 조금 무서웠는데 날도 밝았고, 맨해튼이니 괜찮겠다 싶었다.
어찌 되었든 한 번은 타보아야 하니 구경만 하고 나오자는 생각이었다.
지하철역에 들어가 보니 메트로 카드 자판기가 있었다.
버스와 지하철을 7일간 탈 수 있는 패스를 끊었다.
어댑터
결론적으로 어댑터는 못 찾았다.
220v로 변환해 주는 건 아무 데도 없었다.
그나마 대안으로 찾은 게 The Home Depot이라는 데에 있는 멀티탭이었다.
이렇게 110v짜리 콘센트에 꽂으면 USB C 타입 하나 A 타입 하나, 110v 세 개로 출력해 주는 멀티탭인데, 이 중 USB C 타입만을 위해 이 멀티탭을 사야 했다.. 그래도 충전할 수 있다는 것에 만족...
오늘 길에 CVS에서 일회용 면도기 2세트와 내가 묻히고 들어올 거리 냄새를 호텔 방에서 지워줄 방향제를 사 왔다.
호텔 조식
이제 휴대폰을 충전할 겸 호텔 조식도 먹고, 좀 쉬면서 하루를 시작할 준비를 해야 한다.
조식은 생각보다 괜찮았다.
위 사진의 왼쪽부터:
사과 주스
계란 완숙
스크램블 에그
햄
감자
호밀빵 같은 거에 누텔라
도넛
후르츠
과일들이 다 하나에 담겨있어 후르츠처럼 맛이 다 섞인 게 살짝 아쉬웠지만 나름 각 과일의 맛도 잘 나고 만족스러웠다.
방에 올라와 다시 뷰 사진을 찍으면서 충전되기를 기다린다. 이때가 오전 8시였다.
오전 11시 자연사 박물관
자연사 박물관은 센트럴파크 왼쪽에 위치한 박물관이다.
원래 계획은 자연사 박물관을 두 시간 정도 둘러보고, 오후 한 시쯤에 점심을 포장하여 센트럴 파크 위쪽에 있는 관광 지점들에 가서 낭만 있게 점심을 먹을 생각이었다.
하지만 예상치 못한 자연사 박물관의 방대한 규모에 짓눌려 이 계획은 전면 철폐해야 했다.
자연사 박물관에 대한 내용을 쓰다 보니 포스트가 너무 길어져 별도의 포스트를 작성하였다.
https://hyuni.dev/posts/xqj8mhTDg9DezzRv8PQs
이 포스트에서는 간략히 소개하겠다.
입장
정문부터 규모가 남다르다. 이때 박물관 보려면 하루종일 걸린다는 걸 눈치챘어야 했는데..
자연사 박물관은 구글과 제휴되어 있어서 무료 입장권을 받을 수 있었다.
이렇게 제휴된 박물관이 몇 군데 있는데 출장 왔을 때 최대한 찍어볼 계획이었다.
관람
동물들, 지구, 암석, 광물, 공룡 등등 관람할 게 너무 많아 후기글에도 다 담지 못했다.
밀림에서 사는 동식물 위주로 전시되어 있는 작은 전시관이었다.
뱀, 박쥐, 새 등의 동물이 박제되어 있었다.
나무위키에 대표 사진이 바로 이 티라노사우르스인 듯한다.
이 외에도 스테코 사우르스, 트리케라톱스 등의 공룡들이 전시되어 있었다.
더 자세한 자연사 박물관 후기는 다음 포스트에서 다루었다.
https://hyuni.dev/posts/xqj8mhTDg9DezzRv8PQs
오후 2시 40분 점심
자연사 박물관을 돌아다니는 것이 너무 힘들어 박물관 매점에서 점심을 먹었다.
콜라는 뚱캔 정도 되는 양인 것 같았고, 샌드위치는 무난했다.
버펄로 치킨 랩은 셀러리가 들어있어서 두 입 정도 먹고 버렸다.
초콜릿 쿠키는 나중에 호텔에 돌아가 먹었는데 아주 맛있었다.
오후 3시 센트럴 파크
점심을 빠르게 먹고 메트로폴리탄 박물관을 향해 센트럴 파크를 가로질러 갔다.
원래는 센트럴 파크 위쪽을 돌아볼 예정이었지만 자연사 박물관에서 시간이 너무 지체되고, 다리가 버텨줄 것 같지 않았다.
Belvedere Castle에서 바라본 Turtle Pond이다.
거북이는 못 보고 오리들은 있었다.
구름이 조금 끼기는 했지만 날씨가 나쁘지 않았다.
무엇보다 도심에서 나는 냄새가 여기에서는 덜해서 좋았다.
Cleopatra's Needle이라 불리는 오벨리스크이다.
이집트에서 세워진 이후 1881년에 뉴욕으로 옮겨졌다고 한다.
메트로폴리탄 박물관에 거의 도달했을 때 등장하는 Greywacke Arch이다.
조금 기다리면 뒤에 사람이 없을 때를 노려 사진을 찍을 수 있었지만 다리가 너무 아파 서 있는 시간을 조금이라도 단축시켜야 했다.
오후 3시 30분 메트로폴리탄 박물관
센트럴 파크를 가로질러 드디어 메트로폴리탄 박물관에 도착했다.
자연사 박물관에 비견될만한 엄청난 규모...
지도에서도 봤지만 실물로 보니 정말 컸다.
그나마 다행인 건 여기는 역사와 예술 위주의 전시라 크게 흥미 있을 것 같진 않았다.
금방 보고 나오면 괜찮겠지...라는 생각을 하며 가는 순간!
기부 요구
어떤 남자가 불러 세우더니 이름이 뭐냐고 물었다.
손에 뭔가를 가득 들고 있어서 느낌이 싸했지만 인파가 많은 곳이라 안전할 것 같아 말해주었다.
영어로 발음하기 힘든 이름이라 되묻더니 갑자기 Sweetie라고 부른다고 하더니 멋대로 사인해 주겠다고 한단다.
내 이름도 아닌 것을 적고 사인이라고 받으라고 하더니 QR이 있다고 찍어보란다.
너무 의심스럽다. 요즘 세상에 누가 아무 QR이나 찍을까.
뭐냐고 물어보니 뭐를 위해 몇 달러를 기부하는 거라고 한다.
바로 됐다고 하고 무시해 버렸다.
뒤에서 나를 불렀는데 미국이라 좀 무서웠지만 인파가 많은 곳이라 괜찮겠지 하면서 지나쳤다.
그리고 나중에 박물관에서 나올 때는 이쪽 길로 오지 않았다ㅋㅋ
입장
여기는 자연사 박물관과는 다르게 깔끔했다.
그런데 눈을 사로잡는 문구가 있었다.
LINEAGES KOREAN ART AT THE MET이라는 문구가 벽에 있었다.
다른 건 안 보더라도 저건 봐야겠다는 생각을 하며 입장권을 위한 줄을 섰다.
줄이 길었지만 생각보다 빨리 빠져 금방 입장권을 받을 수 있었다.
이 박물관도 회사와 제휴가 되어 있어 무료로 입장 가능했다. 회사 만세! (한국도 좀...)
관람
메트로 폴리탄 박물관은 이렇게 예술품 위주의 전시가 많았다.
덕분에 적당히 넘어갈 수 있었다.
중간에 이런 큰 광장이 있었는데, 여기를 기준 삼아서 관람하면 되겠다고 생각했다.
하지만 나중에 보니 이런데가 한 두 군데가 아니었다..
다른 광장에는 이렇게 이집트풍의 건축물이 있었다.
사람들이 줄을 서서 사진을 찍었는데, 나는 너무 힘들어서 옆에서만 찍고 지나갔다.
결국 메트로폴리탄 박물관은 절반도 못 보고 나왔다.
더 이상 늦어지면 몸도 봇 버틸뿐더러 해가 져 어두워질 것 같았다.
뉴욕의 무서운 이야기를 전해 들은 한국인에게 어두운 뉴욕 밤거리는 공포였다.
오후 5시 파이브 가이즈
버스를 타고 파이브 가이즈를 먹어보러 갔다.
한국 파이브 가이즈와 비교해보고 싶다는 이유였는데 큰 문제가 두 가지 있었다.
나는 한국의 파이브 가이즈를 먹어본 적이 없다
두 파이브 가이즈의 차별점은 감자인데, 감자를 안 시켰다
결국 비교는 없이 파이브 가이즈 첫인상이 되어버렸다.
여기는 특이하게 땅콩 무한리필이었다.
오피스가 있는 역삼역 근처에 바스버거가 있는데, 거기에서는 감자칩이 무한리필이다.
그 감자칩이 너무 맛있어서 계속 퍼다 먹는데, 여기서는 땅콩이 그런 포지션인가 보다.
왼쪽에서 메뉴를 보고 주문하고, 오른쪽에서 번호를 불러주면 받는 구조이다.
주문할 때 서브웨이처럼 들어갈 재료들을 선택해야 한다.
나는 치즈 버거에 토핑은 All the way에서 버섯을 빼달라고 하였다.
치즈버거니 당연한 건가..?
야채가 없었고 버섯이 많았다. 분명 버섯 빼달라고 했는데...
버거도 기름졌지만 포장지에도 기름이 가득 묻어있었다.
이게 미국인가...
거리에서 나는 냄새로 속이 안 좋았는데 버거마저 너무 기름지니 더 먹을 수가 없었다.
반쯤 먹고 매장을 나섰다.
오후 6시 호텔 복귀
호텔로 돌아와서 좀 쉬면서 다음 날 계획을 세웠다.
오늘 못 가본 곳을 갈지 아니면 원래 계획대로 할지를 고민했다.
고민은 오래가지 않았다.
오늘 너무 많이 걸었다.
내일은 좀 쉴 수 있는 계획을 세우면서 자연사 박물관에서 사 온 초콜릿 쿠키를 먹었다.
출장에서의 마지막 휴일을 위해...
02024. 10. 08.

일상
교보 문고에서 내 책 2쇄본을 찾았다 (집필 / 출판 후기)
2023년 2월 24일, 내 인생 첫 책이 출간되었다.
길벗 출판사에서 기획 출판으로 출간한 [취업과 이직을 위한 프로그래머스 코딩 테스트 문제 풀이 전략: 자바 편]이다.
1쇄로 3,000권을 발행했는데, 그로부터 1년 반 후인 2024년 8월 19일에 2쇄를 발행하게 되었다.
오늘 회사 지인의 결혼식을 참석한 후, 몇 명이서 교보 문고를 들르게 되었는데 문득 내 책의 현황이 궁금했다.
마침 2쇄를 찍은 지도 얼마 안 되기도 했고, 2쇄를 1쇄가 완전히 나가기 전에 찍어서 교보 문고에 몇 쇄의 책이 있는지가 궁금해졌다.
실제로 서점에 전시되어 있는 모습도 보고 싶었다.
교보 문고의 도서 검색으로 책의 위치를 찾았다.
이런 식으로 책의 제목과 저자 이름, 출판사와 출판일, 가격 등의 책 정보와 함께 도서의 위치가 그림과 함께 출력된다.
여기에 적혀 있는 출판일인 2023. 02. 23은 초판 발행일이다.
추가적으로 발행한 부수인 건 상관없이 출판일 기준인 것 같은데, 생각해 보니 그게 말이 되는 듯..
여하튼 해당 위치로 가서 책을 발견할 수 있었다.
내 책 두 권이 자바 코너에 꽂혀있는 것을 발견했다.
평대 하단에서는 책을 못 찾았는데,
누군가 평대 하단에서 꺼내서 보고 벽면 하단에 꽂아놨거나,
누군가 평대 하단에 있는 책을 사갔거나...!
개인적으로는 후자면 좋겠지만 일단 뭔가 책이 물리적으로 움직이고 있다는 생각을 하니 새삼 신기했다.
(심지어 두 권 중 왼쪽에서는 자세히 보면 펼쳐서 접힌 흔적을 발견했다. 누군가는 펼쳐보았다!)
서점의 책을 확인해 보니 2쇄 발행된 책이었다.
서점에서 2쇄 책을 처음 보기도 했고, 같이 간 회사 친구들이 반응을 너무 잘해줘서... 기념사진을 한 장 찍었다.
내 책도 발견하고 기념사진도 찍은 김에 집에 돌아와 새벽 감수성을 빌어 집필과 출간 과정에 대한 후기를 남겨보고자 한다.
출간 후기
2022년 4월 중순 즈음에 처음으로 출판사와 연락을 시작하고, 샘플 원고와 계약을 거쳐 6월 중순에 본격적으로 집필을 시작했으니 약 9개월에 걸친 집필이었다.
책을 쓰기 위한 기간으로는 짧다면 짧다고 할 수 있는 이 기간 동안 600페이지가 넘는 책을 쓰는 일은 생각보다 쉽지 않았다.
P가 벌린 일은 내면의 작은 J가...
내 다른 게시글에서도 언급했지만, 사실 이전에도 몇 번씩 책을 써보려고 시도했던 적이 있었다.
https://hyuni.dev/posts/qqK2tlLCrOyYAuahj8FY
하지만 나는 극 P의 MBTI이다. 마음이 이끄는 대로 행동한다.
가슴이 시켜서 책을 써보는 것을 시작했다가, 열정이 식어서 그만두고, 다시 가슴이 시키는 다른 주제로 처음부터 다시 시작하는 것을 반복했다.
결국 초반을 넘어가는 것이 없었고, 책은 정말 꾸준하고 집필에 대한 열망이 있는 사람들만이 쓰는 것이라 생각하게 되었다.
그러다 출판사에서 작가를 모집한다는 소식을 듣자, P의 주도하에 지원해 버리게 되었다.
강제성이 부여되자 중간에 열정이 식어도 그만둘 수가 없었다.
출판사와 계약은 했고, 책은 써야 하니 내면에 존재하는 작은 J가 자기도 존재함을 알려왔다.
하기 싫다는 생각, 귀찮다는 생각은 묻어두고 해야 한다는 생각을 갖게 되었을 때 책이 써졌다.
사실 이런 부정적인 생각은 컴퓨터 앞에 앉기 전까지만 있었고, 막상 글을 쓰기 시작하면 집중이 잘 되고 잘 써졌다.
즉 책상에 앉기까지가 문제였던 것인데, 밍기적 하는 나를 내면의 작은 J가 억지로 끌어다 앉힌 것이다.
한 번 앉고 글을 쓰기 시작하면, P는 거기에 동화되어 다시 열정이 되살아나는 듯했다.
생각해 보면 이때까지의 나의 삶은 다 이런 형태로 진행된 것 같다.
하고 싶은 게 생기면 바로 일을 벌이고, 여기에 강제성이 있다면 어떻게든 해결하려고 하는 과정에서 성장하는 것 같다.
물론 강제성이 없어서 중간에 엎는 것도 모두 나를 성장시켜 준 과정이라고 생각한다.
아예 시도조차 하지 않고는 그 작업이 어떤 느낌인지, 어떤 생각으로 임해야 하는지를 알 수 없다.
조금씩이라도 해보는 것 하나하나가 경험이 되고 쌓인다.
책을 쓸 때의 마음가짐
주변에 개발자를 준비하는 사람들이 많이 있었다.
개발에 뜻이 있는 소수도 있었지만 대부분 개발자의 균형있는 워크 라이프 밸런스, 컴퓨터만 있으면 어디서든지 할 수 있는 자율성 등에 현혹된 경우였다.
그런데 모두들 공통적으로 대우 받는 개발자가 되기 위해서는 코딩 테스트를 필수로 준비해야 한다는 것을 알고는 있지만, 코딩 테스트에 대한 장벽을 너무 높게 느꼈다.
프로그래밍 공부도 어려운데 코딩 테스트는 더 난이도 있고 어려운 것이라 생각하는 것이다.
여기에는 일부 동의한다.
코딩 테스트는 당장 눈에 보이는 개발보다 확실히 공부할 맛이 안나고 해봤자 별로 쓸데도 없는 것 처럼 느껴진다.
하지만 개발자는 열심히 작성한 코드를 엎고 고쳐 쓰고, 다시 엎고 고쳐쓰는 과정을 통해 프로젝트에 눈에 띄는 변화는 없어도 본인은 한 단계씩 성장한다.
코딩 테스트를 공부하는 것도 당장은 어렵고 성취감이 적을지라도 그 과정에서 알게 되는 여러 알고리즘과 자료 구조, 시간 복잡도와 효율성, 특히 그 무엇보다 문제를 파악하고 해결해 나가는 사고의 성장이 분명히 일어난다.
코딩 테스트를 단순히 코딩 테스트 문제에서 정답이 뜨는 코드를 작성하기 위한 과정이라고 생각하면 안된다.
문제를 해결하는 코드 중에서도 더 좋은 코드, 더 언어를 잘 활용한 코드를 작성하려고 시도하고 노력하는 것으로 우리는 성장할 수 있다.
나는 코딩 테스트 책을 쓸 때 이러한 관점에서 집필했다.
읽으면 쉽게 이해할 수 있도록 가독성을 최대한 신경 쓰고, 자바의 특징을 잘 살린 코드를 보여주려 고군분투했다.
나는 이 부분이 내 책이 시중의 다른 책에 비해 갖는 강점이라 생각하고, 그렇기 때문에 이 강점을 더 잘 살리기 위해 좋은 코드에 더 집착했다.
개발자를 준비하는 사람이라면 이 책은 여러 번 읽어볼 만한 가치가 있다고 자부한다.
물론 단순히 코딩 테스트용 지식을 이해하기 위해 여러 번 읽는 것은 아니다.
책 중간 중간에 나의 사고 방식에 대한 내용, 코드를 작성할 때 신경 쓴 점들, 언어의 특징을 살려서 작성한 코드들이 있다.
이런 부분들을 보다 보면 내가 말하고자 하는 좋은 코드는 무엇인지, 그리고 스스로 생각하는 좋은 코드가 무엇인지에 대한 고민을 자연스럽게 할 수 있을 것이다.
다음 책을 쓰기로 했다
책을 쓰는 과정은 힘들지만 절대 싫지는 않았다.
공식적으로 출판된 책의 저자가 된다는 설렘을 주었고,
평소에 생각만 해오던 나의 의견과 학습 방향을 스스로 정리하게 해주는 기회였으며,
내 글이 세상 밖으로 나온다는 흔한 이야기에 그만큼 진실된 감정이 담겨있기에 흔해질 수 있었다는 것을 깨닫게 해 주었다.
무엇보다 글을 쓰는 것이 재미있었다.
책을 쓰면서 글을 쓰는 것이 프로그래밍이랑 비슷하다는 생각을 했다.
내가 생각하는 내용을 정리하고, 표현하고, 그 과정에서 읽는 사람들이 잘 이해할 수 있을지를 고민해야 한다는 집필과 프로그래밍의 공통점이 글을 쓰는 것에 대한 심리적 장벽을 많이 낮춰주었다.
그래서 글을 써보고 싶은 주제가 떠올랐을 때 대략적인 목차를 구성해 길벗에 전달했다.
다행히 길벗에서도 주제를 마음에 들어 해 주셔서 목차와 분량 등만 이야기하고 다음 책을 집필하기로 계약했다.
이렇게 또 P가 한 건 벌여놨으니 이제 J가 힘내서 작업을 마무리해야지...
02024. 10. 03.

일상 > 뉴욕 출장기
2일차 - 그랜드 센트럴 스테이션, 모마 미술관, 서클라인 크루즈 (2024년 9월 1일)
뉴욕에 온 지 실질적 이틀차.
아직 일요일인 만큼 열심히 놀러 다녀야 하지만 어제의 빡센 일정 때문에 이 날은 좀 쉬엄쉬엄 할 수 있는 일정을 짰다.
브라이언트 공원 -> 그랜드 센트럴 스테이션 -> 모마 미술관 -> 크루즈 관광으로 이어지는 루트이다.
모마가 10시 30분 오픈이고, 크루즈 예약을 3시에 했기 때문에 모마 가기 전 혼자 둘러볼 수 있는 것들은 최대한 둘러보고, 모마를 본 후 호텔에 들러서 쉬면서 휴대폰을 충전하고, 크루즈에 가는 일정이다.
오전 7시 30분 기상
언제나처럼 호텔에서 바라본 뷰로 하루를 시작한다.
크루즈를 타러 가기로 한 날인데 날씨가 심상치 않다.
걱정되는 마음으로 호텔 조식을 먹으러 이동.
조식 구성은 전날과 다르지 않다.
다만 이번에는 다른 공간에서 먹었는데, 호텔 2층에 테라스가 있었다.
야외 분위기라 쾌적하게 먹을 수 있었다.
오전 9시 브라이언트 공원
뉴욕에 가면 브라이언트 공원을 꼭 들러야 한다는 말이 많았다.
마침 그랜드 센트럴 스테이션을 가는 길에 있길래 들러보았다.
처음 본 브라이언트 공원은 생각보다는 작았다.
브라이언트 공원 뒤쪽에는 도서관이 있는데, 이 도서관이 인테리어가 이쁘게 되어있는 듯해서 가보고 싶었으나 일요일엔 안 열었다..ㅠ
나중에 안 사실이지만, 이 도서관은 예약을 해야 입장할 수 있다고 한다.
예약하지 않은 나는 열었어도 못 가는 거였으니 오히려 다행...
공원을 둘러보는데 역시나 누군가가 의자에 앉아 약물을 피우고 있었다.
뉴욕에서는 꽤나 자주 보이고 냄새도 많이 나는 약물...
전날 거리를 돌아다니며 그래도 많이 익숙해진 나는 자연스럽게 빨리 지나쳐갔다.
오전 9시 10분 그랜드 센트럴 스테이션
브라이언트 파크에서 얼마 걷지 않아 그랜드 센트럴 스테이션에 도착했다.
정문에 긴 줄이 있었는데, 설마 줄을 서야 하는 건가 했는데 아마 극장 줄인 것 같았다.
내부가 생각보다 넓고 길 찾는 게 어려웠다.
딱히 내부 지도도 없어서 무작정 걸어 다니는 수밖에 없었다.
큰 기차역이라고 해서 서울역 정도 생각했는데, 그보다 훨씬 크고 복잡한 듯했다.
그랜드 센트럴 스테이션의 유명한 관광 명소 Whispering Gallery이다.
볼록하게 생긴 천장은, 시공 당시에는 의도하지 않았지만 한쪽 끝에서 이야기하는 소리를 모아 반대쪽에 효과적으로 전달하는 구조라고 한다.
실제로 여러 명이서 온 사람들은 시도해 보는 것 같았는데, 나는 혼자 가서 해보지는 못했다.
한참을 돌아다니니 드디어 메인 공간이 나왔다.
큰 공간에 한쪽에는 매표소, 다른 한쪽에는 기차를 탈 수 있는 승강장이 있었다.
동쪽과 서쪽에는 각각 Easy Balcony와 West Balcony라고 하는 구조물과 아래층으로 내려가는 계단이 있었다.
웬만큼 둘러보고 나서 모마에 가기 전 좀 쉬기로 했다.
지하로 내려가면 나오는 상가들 중에서 tartinery를 들러보기로 했다.
시트러스 스퀴즈라는 이름의 오렌지, 자몽, 레몬을 갈아 만은 주스를 시켜보았다.
말 그대로 오렌지와 자몽을 섞은 맛이었는데 매우 셨다.
평소에 신걸 잘 먹는 편이라 나름 맛있게 먹었다.
다만 별로 시원하지 않은 건 조금 아쉬웠다.
오전 10시 15분 모마 미술관
길을 헤맬 것을 감안해서 일찍 출발했더니 오픈 전에 모마에 도착했다.
아직 오픈 전인데도 사람들이 입장 줄을 서있었다.
모마는 현대 미술관답게 앞서 방문한 다른 두 박물관과 비교해 깔끔했다.
왼쪽이 매표소, 오른쪽이 입장이었다.
회사 제휴로 공짜 입장!
가장 기분 좋은 순간이다.
티켓을 받으면 다시 입장을 위한 줄을 서야 한다.
줄이 금방금방 빠져 빠르게 입장할 수 있었다.
입장은 했어도 아직 오픈 전이라 대기해야 했다.
이때가 10시 20분이라 약 10분 정도 대기했었다.
그래도 대기를 위해 의자와 소파 등을 많이 마련해 놔서 편하게 대기할 수 있었다.
갑자기 현대 카드 로고가 보여 멈출 수밖에 없었다.
현대 카드를 통해서 한국의 미술품들 몇 점이 모마에 전시된 듯하다.
그리고 둘러보았는데...
역시나 나는 현대 미술에는 영 흥미가 없는 것 같다...
더 이상 있다가는 크루즈로 바로 가야 할 것 같아 빨리 호텔에서 쉬면서 크루즈에 갈 준비를 하는 게 나을 것 같았다.
마지막으로 모마 스토어에서 기념품을 샀다.
한국에서는 삼성페이의 힘으로 카드를 하나도 들고 다니지 않아도 됐지만, 여기에서는 무려 4개의 카드를 들고 다녀야 했다.
내 신용 카드, 법인 카드, 메트로 카드, 호텔 키를 모두 들고 다니기 위해서 샀다.
사실 색깔이 구글 색이랑 비슷해서 샀다.
하얀색으로 깔끔하고 이쁘게 생겨 샀다.
사놓고 멍청하게도 크루즈에는 안 가져갔다.
오후 12시 20분 점심
점심으로는 호텔 근처에서 피자를 먹었다.
조각 피자를 파는데 받아서 서서 먹거나 가져가는 매장이었다.
치즈 피자 하나, 페퍼로니 피자 하나, 콜라 한 캔을 주문했는데, 피자 두 조각에 $5도 안 했던 것 같다.
피자는 얇고 크고 간은 조금 짠 편이었다.
내 앞에 있던 사람이 핫 소스를 뿌리다 피자 한 조각을 그대로 떨어뜨려서 혹시라도 눈 마주칠까 조심히 먹었다.
오후 2시 40분 타임 스퀘어 부근
크루즈를 타러 가기 위해 타임스퀘어에서 버스를 타야 했다.
문제는 버스 정류장이 어디인지를 모르겠고, 버스도 안 왔다.
사람과 자동차가 심각하게 많아 I인 나에게는 너무 기가 빨리는 거리였다.
어디서나 나는 약물 냄새는 덤이었다.
아무리 기다려도 버스는 안 오고, 시간은 속절없이 흐르고...
크루즈에 늦지 않게 가야 하는데 애가 탔다.
다행히 한참 걸어서 다른 정류장을 찾아 버스를 탈 수 있었다.
타임스퀘어의 첫인상은 별로 좋지 않게 남아버렸다.
오후 3시 15분 서클 라인 크루즈
발권 / 탑승
늦지 않게 크루즈에 도착해서 티켓을 받았다.
내가 예매한 크루즈는 서클 라인 Best of NYC이다.
맨해튼을 한 바퀴 도는 크루로, 맨해튼의 서쪽에서 출발하여 반시계방향으로 돌며 2시간 30분 동안 관광한다.
중간에 자유의 여신상도 볼 수 있고, 맨해튼 전체를 돌기 때문에 마음 편하게 관광하려고 선택했다.
나중에 확인해 보니, 맨해튼을 한 바퀴 도는 경로가 구글 지도에 확실하게 남아있었다.
덕분에 크루즈가 어떻게 이동했는지가 머릿속에 각인되었다.
나는 프리미어는 전용 좌석이 있다고 해서 뷰를 더 잘 보기 위해 프리미어 티켓을 끊었다.
위 사진에서 보이는 붉은색 좌석이 프리미어 전용 좌석이고, 초록색이 일반 좌석이다.
보면 알겠지만 큰 차이 없다.
굳이 차이라면 배가 맨해튼을 반시계 방향으로 돌기 때문에 맨해튼은 좌측 창문으로 보인다.
하지만 막상 자유의 여신상은 오른쪽에서 보인다. \
결국 거기서 거기...
나는 프리미어 좌석 중 창가 자리에 앉을 수 있었다.
관광
분명 아까 타임스퀘어에서만 해도 날씨가 흐렸는데 갑자기 맑아졌다.
심지어 모마에 있을 때는 비까지 왔었는데?
갑자기 맑아진 걸까 아니면 모든 구름이 맨해튼에 모여있는 걸까.
날이 점점 좋아진다.
저 멀리 고층 빌딩에 둘러싸인 베슬도 보인다.
이번 출장에 가보지는 못했지만 멀리 서라도 봤으면 됐지 뭐...
맨해튼은 강을 끼고 있어 중간중간 부두(pier)가 매우 많다.
부두에는 순서에 따라 숫자로 이름이 붙어있는데, 위 사진은 Pier 40을 지날 때이다.
요트 한대가 유유히 지나가는 모습이 평화로웠다.
저 멀리 고층 빌딩들이 보이기 시작한다.
세계 무역 센터 (World Trade Center)가 있는 월 스트리트이다.
사진 속 오른쪽에 가장 높이 뾰족하게 솟아난 건물이 세계 무역 센터이다.
그리고 배가 드디어 자유의 여신상을 지나갔다.
자유의 여신상만 단독으로 찍은 사진도 있지만, 이 사진이 더 당시의 분위기가 있는 것 같다.
날씨는 매우 좋았고, 2층 뒤의 좌석에는 사람들이 사진을 찍느라 분주했다.
나는 배 왼쪽에 있었고, 자유의 여신상은 오른쪽에서 보이기에 자리에서 일어났는데, 이때를 기점으로 여기저기 돌아다니기 시작했다.
호텔에서 비축해 둔 체력으로 배 안을 돌아다니면서 사진을 찍는 도중, 충격적 이게도 1층으로 가면 배 앞으로 나갈 수 있는 것을 발견했다.
1층으로 나오니 앞에 걸리는 것 없이 배가 진행하는 방향으로의 시야가 뻥 뚫려있었다.
이때부터 크루즈 끝까지 계속 여기에 서있었다.
크루즈는 환상적이었지만, 프리미어 티켓은 정말 가치가 없었다...
날씨도 좋아 밖으로 나간 후부터 사진을 미친 듯이 찍기 시작했다.
뉴욕에서 찍은 대부분의 사진은 크루즈에서 찍은 사진이다.
위 사진은 왼쪽에 테란의 불 탄 배럭 같은 게 있길래 찍어보았다.
햇빛이 강렬하여 선글라스를 착용했다.
저 멀리 오른쪽에 펩시 콜라 로고가 있길래 마침 들고 있던 펩시 콜라를 들고 찍었다.
날씨와 뷰, 바람과 강물, 지나가는 배까지 너무 평화롭고 환상적이었다.
무엇보다 여기서는 거리에서 나는 이상한 냄새들이 나지 않았다.
강을 기점으로 맨해튼과 다른 지역이 나누어지다 보니, 지역의 색깔 차이가 확실했다.
섬인 만큼, 다리가 매우 많았다.
어디를 찍던 자랑할만한 사진이 나왔는데, 맑은 날씨의 하늘이 하드캐리했다.
한국은 지금 글을 쓰고 있는 9월 20일까지도 한여름이지만, 뉴욕은 하늘만큼은 이미 가을이었다.
그냥 오래되고 녹슨 다리 같지만 맑은 날씨와 평화로운 분위기에 뉴욕 버프까지 받으니 고풍스러워 보였다.
또 다른 다리.
이 다리는 더 크고 현대적으로 생겼다.
다리를 지나면 이렇게 걸리는 것 하나 없이 시야가 확 트인다.
멍하게 바람과 물을 만끽할 수 있었다.
고층 건물들이 보이기 시작한다.
센트럴 파크 기준으로 위쪽은 할렘가여서 우리가 여행 가면 보통 절대 가지 말라는 위험지역이다.
위쪽 사진은 그보다 조금 내려온 곳으로, 센트럴 파크 기준 왼쪽, Upper West Side이다.
현지인 말로는 이 지역은 부자촌이라 매우 살기 좋고 안전하다고 한다. (아시안 기준으로는 안 찾아봐서 모르겠다)
확실히 뭔가 건물들이 예쁘다.
밖에 있었는데 거의 도착했으니 모두 실내로 들어오라고 했다.
드디어 맨해튼 한 바퀴를 전부 돌아 출발 위치로 되돌아왔다.
후기
최고였다.
비록 편하게 관광하려고 예약한 2시간 30분짜리 크루즈에서 2시간 동안을 서있었지만, 그만한 가치가 있었다.
평소에 잘 남기지 않는 후기도 정성껏 남겨주었다.
가운데 Hyuni_K가 내가 남긴 리뷰이다.
당시에 남긴 리뷰에도 프리미어는 사지 말고 앞에 실외로 나가라고 했다.
내 위의 리뷰는 나처럼 좋은 날씨에 가서 아주 기분 좋아 보이지만, 안타깝게도 아래에 있는 리뷰는 날씨의 혜택을 받지 못했나 보다.
맨 아래 리뷰는 나래이터에 대해 불평하고 있지만 나는 나래이션을 안 들어서 잘 모르겠다.
들어보려고 시도는 해봤는데, 워낙 빠르게 말하기도 하고 방송을 타고 나오는 거라 거의 못 알아들었다.
Circle Line Cruise... 나중에 갈 일 있으면 꼭 기억해 둬야겠다.
오후 7시 저녁
저녁으로는 맥도날드를 가봤다.
한국의 맥도날드와 비교해보고 싶었다.
전 날의 파이브가이즈는 한국에서 안 먹어본 안일함과 뉴욕의 거리 냄새로 인한 매스꺼움 때문에 실패했지만, 맥도날드는 많이 먹어봤으니 비교할 수 있으리라 생각했다.
내부는 생각보다 너무 똑같이 생겼다.
심지어 키오스크도 똑같이 생겼다.
자세히 보고 영어가 쓰여있는 걸 모른다면 그냥 한국의 맥도날드인 줄 알 것 같다.
뭔가 미국만의 햄버거가 있는지 찾아봤지만 잘 모르겠어서 그냥 비교용 빅맥을 시켰다.
여기는 빨대를 준다!
종이 빨대이긴 한다.
감튀는 똑같이 생겼다.
맛도 비슷한 것 같다.
다른 음식은 다 간이 세던데 막상 맥날 감튀는 한국이 조금 더 짭조름한 것 같다.
똑같이 생겼다.
버거도 똑같다.
심지어 소스 많이 안 넣어주는 것까지 똑같다.
원래 빅맥에는 소스가 많이 없나?
맛도 똑같았다.
마무리
크루즈를 앉아서 탔으면 괜찮았겠지만 계속 서있어서 전혀 휴식이 안 됐다.
다음 날을 위해 일찍 쉬기로 했다.
02024. 09. 20.

일상
뉴욕 자연사 박물관 다녀온 후기
자연사 박물관은 센트럴파크 왼쪽에 위치한 박물관이다.
원래 계획은 자연사 박물관을 두 시간 정도 둘러보고, 오후 한 시쯤에 점심을 포장하여 센트럴 파크 위쪽에 있는 관광 지점들에 가서 낭만있게 점심을 먹을 생각이었다.
하지만 자연사 박물관을 돌아다니며 말도 안되는 계획이라는 걸 깨닫기 까지는 얼마 걸리지 않았다..
입장
자연사 박물관까지는 버스를 타고 이동했다.
아침에 사둔 메트로카드가 바로 한 역할 해주었다.
정문을 들어서자 바로 웅장한 공룡 뼈가 나타났다.
생각보다 흥미로울 것 같은 예감이 들었다.
회사와 박물관이 제휴돼있어서 무료로 입장할 수 있었다.
General Admission이 가장 기본적인 입장료인데, 이 가격만 해도 3만원에 달하는 것을 생각하면 상당한 듯?
General Admission에 더해 추가적인 관람을 할 수 있는 패스들이 있는데, 해볼까 하다가 그냥 이걸로 만족하기로 했다.
그런데 이것만 해도 볼게 너무 많아서 나중에는 안하길 천만 다행이라는 생각이 들었다.
관람
상당히 많은 전시관이 분류별로 있었다.
동물들
이런식으로 꽤 퀄리티 좋게 박제된 동물들이 전시돼있다.
뭔가 얼굴이 너무 억울해보이는 호랑이.
귀가 안보여서인가 눈이 순해보여서인가.
눈이 순해서인 것 같다.
파충류관은 상대적으로 다른 전시관들에 비해 약한 듯 했다.
박제보다는 모형이 많았고, 모형도 모형 티가 좀 많이 났다.
그래도 이런 건 멋있었다.
이 외에도 지역별, 시대별, 종류로 전시관이 나뉘어있는데, 너무 많고 넓다.
꼭 충분한 시간을 확보해놓고 와야 할 듯 한다.
지구와 우주
빅뱅부터 시작해서 지구가 어떻게 형성됐는지, 암석들이 어떻게 변형되는지 등에 대한 내용들이 있었다.
달의 형성 과정에 대한 이론 중 하나도 이렇게 전시돼있었다.
달이 하루만에 생겼다니 놀라웠다.
나무가 땅에 묻혀 오랜 시간이 지나며 결정화된 모습이다.
실제로 만져볼 수 있게 전시되어 있는데, 매우 단단하고 돌 같은 촉감이다.
문명과 문화
여러 문명과 거기에서 발전된 문화들에 대한 내용도 전시되어있다.
이쪽은 크게 관심이 없어서 사진만 몇 장 찍고 빠르게 넘어갔다.
뼈와 화석
다양한 동물들이 진화한 흔적을 뼈에서 찾는 내용들이 전시되어 있었다.
이처럼 동물의 뿔의 형태에 따른 분류를 해놓기도 했다.
이미 멸종된 동물의 뼈를 모아 복원시켜 놓은 모습이다.
중간 공동
여기가 나왔을 때 조금 절망스러웠다.
진짜 오래 걸으면서 많이 봤는데 이 곳에 도달하니 아직 반도 못보고 훨씬 많이 남았다는 것 같았다.
그리고 이대로는 안되겠다 싶어서 박물관 팜플렛을 챙겨 아직 보지 않은 전시관 위주로 돌아다니기 시작했다.
공룡
개인적으로 자연사 박물관의 메인이라고 생각한 공룡!
이 공룡관에 진입한게 무려 오후 1시 40분이다.
두 시간 안에 보고 센트럴 파크에서 점심을 먹자는 내 계획은 다른 전시관들에서 장장 2시간 30분을 소요하며 무너져 내렸다.
공룡들의 전시 상태는 좋았다.
확실히 흥미롭게 전시해놓았다는 생각이 든다.
거북이의 조상인 공룡이겠지?
거북이의 얼굴 뼈가 저렇게 생긴 걸 처음 알았다.
얘도 거북이 조상인가..?
다른 관에서 목과 꼬리가 매우 긴 공룡을 만났다.
목이 상당히 길어서 꼬리와 함께 찍을 수가 없다
파노라마로 겨우 찍었다.
목이 너무 길어 전시관 밖으로 나가있다.
전시관 밖으로 나가니 드디어 머리가 보인다.
모든 공룡 중에 가장 유명한 티라노사우르스에서 기념샷을 찍었다.
지금 찾아보니 나무위키에 있는 티라노사우르스 사진(오른쪽)이 바로 이 티라노사우르스인 듯 하다.
최근에 티라노사우르스가 사실 입술이 있어서 이빨이 안보였을 것이라는 주장이 나와 사실 귀여운 (순하진 않았겠지만) 생물이었다는 인식이 생기기도 했다.
광물
공룡도 봤겠다 배가 너무 고프고 다리도 아파 이제 밥을 먹으러 가야겠다는 생각이 들던 찰나, 광물관을 발견했다.
저 안에서 빛나는 광물과 보석이라는 글자를 보고 차마 지나칠 수 없었다.
빨리 보고 나오자는 생각으로 들어갔다.
이렇게 많은 광물들을 잘 화려하게 전시해 놓았다.
엘바이트(Elbaite)가 뭔지, 전기석(Tourmaline)이 어떤 뜻인지는 모르겠지만 예쁘다.
같은 광물을 베이스로 하더라도 어떤 성분이 섞이느냐에 따라 다른 색이 나올 수 있다고 한다.
여기서부터는 정말 몸이 한계에 다다라 되돌아왔다.
점심
어디 나갈 힘도 없고 배도 고파 그냥 자연사 박물관 안에 있는 매점에서 점심을 해결하기로 했다.
콜라와 버팔로 치킨 랩, 샌드위치, 초콜릿 쿠키이다.
콜라는 한국에서 파는 캔보다 길어서 양이 꽤 됐다. 뚱캔 정도 되나?
샌드위치는 무난한 맛이었지만 랩이 함정이었다.
셀러리가 들어있어서 먹기 힘들었다. 결국 두 입 정도 시도해보고 그대로 쓰레기통으로 들어갔다.
초콜릿 쿠키는 나중에 호텔에 돌아가서 먹었는데 매우 맛있었다.
후기
진짜 너무 고되다.
만만하게 보고 갔다가 엄청난 규모에 무릎을 꿇었다.
사실 중간에 배고파서 매점에 갔는데, 줄이 너무 길어 포기했었다.
만약 자연사 박물관을 간다면 매점에 사람 없을 때 미리 음식을 사놓던가 해서 (반입이 되는지는 모르겠다) 중간에 앉아서 먹으면서 쉬는 시간을 필히 갖길 바란다.
제대로 보면 4시간은 훌쩍 간다.
나는 관심 없는 전시관은 대충 보고 했는데도 3시간 반이 걸렸다..
이 포스트에 생략된 사진만 해도 이 백장이 넘는다.
하지만 그만큼 방대한 전시관이 있고, 퀄리티도 매우 좋아 동물이나 공룡, 역사 등을 좋아하는 사람들은 꼭 한 번 가볼만한 곳인 듯 한다.
02024. 09. 13.

일상 > 뉴욕 출장기
0일차 (2024년 8월 30일)
입사 후 4년 3개월 만에 처음으로 출장이 잡혔다.
지금 하고 있는 프로젝트와 관련하여 뉴욕에 일하고 있는 팀과 얘기할 거리가 많은데 한국에서는 시차 때문에 효율이 떨어졌기 때문에 같은 프로젝트를 하고 있는 세 명이 함께 가게 된 출장이었다.
8월 30일 금요일 밤에 인천에서 출발해서 뉴욕 시간으로 9월 7일 오전 1시 비행기로 돌아오는 일정이었는데,
첫 출장 + 첫 뉴욕 시너지로 매우 들뜬 마음이었다. 하지만 그와 함께 총이나 약물 등 무서운 이야기도 많이 들어서 조심히 다녀와야겠다는 생각도 함께 들었다.
월~금 출장으로, 출장 이전 토요일, 일요일을 붙여서 관광을 하기로 했다. 이 신난 마음은 출장을 가서도 변하지 않아 7일간 무려 1,400장이 넘는 사진을 찍고 오게 된다...
첫 출장의 기억을 더 잊기 전에 사진들을 돌아보며 기억을 회상하는 포스팅을 해보고자 한다.
오후 7시 30분 공항 도착
같이 출장 가시는 분이 오피스가 있는 역삼역을 들러 인천 국제공항에 가셔주신다 하여 감사하게도 차를 얻어 타게 되었다.
또 다른 팀원분은 여행용 캐리어를 빌려주셔 편하게 짐을 넣어갔다 올 수 있었다.
이 두 분이 아니었으면 공항 버스를 알아보고, 배낭 하나 메고 힘들게 다녀올 뻔... 감사합니다 여러분
공항에 도착해서 저녁을 먹었다. 제육을 먹고 싶었지만 다 떨어져 해물 순두부찌개를 먹었다.
순두부찌개는 맛있었는데 밥이.. 좀 별로였다. 마치 밥을 지은 다음 물로 한 번 헹궈서 맛을 다 빼버린 느낌?
오후 9시 30분 출국
좌석
9시 반 비행기를 탑승했다.
우리는 에러프레미아라는 항공사를 이용했다.
이코노미 프리미엄이라는 좌석이 있어서 이코노미보다는 쾌적하지만 비즈니스만큼 비싸지는 않았다.
운 좋게 1열 좌석을 예약할 수 있었다.
확실히 이코노미보다 좌우 간격이 넓어 옆 사람과 부딪힐 일이 없었고, 레그룸도 넓었다.
항공사 기념품
에어프레미아의 이코노미 프리미엄은 등받이와 리클라이너도 다른 항공사보다 더 많이 기울어진다고 한다.
이코노미 프리미엄 출시 이후 선착순으로 아로마티카와 콜라보한 기념품을 주었다. (돌아올 때는 못 받았다)
오렌지 향이 나는 스킨케어 제품들이었는데, 립밤은 안 써봤고, 세럼은 향이 좋았고, 크림은 향이 내 취향이 아니었다.
기내식
총 두 번의 기내식이 제공되었다.
첫 번째 기내식으로는 비빔밥을 받았다.
다른 하나는 소고기로 만든 뭐시기였는데 기내식 소고기는 별로일 것 같아 비빔밥을 선택했다.
그릇이 작아 한 번에 비비지는 못하고 참기름만 전체적으로 뿌린 후 부분적으로 고추장을 뿌려 덮밥처럼 먹었다.
디저트로 나온 저 초코 케이크가 부드럽고 달아 맛있었다.
먹고 빨리 자게 맥주를 마셨다.
한참 자고 일어나자 그다음 기내식이 나왔다. 사진에 기록된 시간 기준으로 8시간 반 만에 나온 것 같다.
돼지고기로 만든 뭐시기를 받았다. 다른 하나는 뭐였는지 잘 기억이 안 난다.
밥은 없고 양념된 돼지고기와 감자가 있었다.
당근은 생이었으면 먹었을 텐데 삶은 당근이라 먹지 않았다.
왼쪽 위에는 감자 샐러드가 아니라 코울슬로다.
자몽 주스가 맛있어서 세 잔은 마신 듯하다.
오후 11시 공항 도착
무려 약 14시간 30분 만의 비행 끝에 뉴어크 공항에 도착했다.
뉴어크는 뉴저지에 있는 공항으로 호텔까지 우버를 타고 이동해야 한다.
그런데 여기서 상황이 발생했다.
우버를 분명 깔고 법인카드까지 등록해서 왔는데...
실제로 우버를 호출하려니 본인인증을 해야 한다고 한다.
그런데 eSim을 등록하니 문자 수신이 잘 안 된다.
결국 인국공까지 차를 태워다 주신 분이 우버까지 같이 태워다 주셨다...ㅠㅠ
오전 12시 호텔 도착
내가 묵은 호텔은 하야트 플레이스 뉴욕 첼시이다.
오피스와 가까웠고, 회사와 계약이 되어있어 조금 더 싼 가격에 갔다 올 수 있었다.
하지만 그럼에도 방과 서비스에 비해 20만원이 넘는 매우 높은 가격이었는데, 뉴욕의 모든 호텔이 그러하다 하더라..
방 둘러보기
방을 둘러보는 영상도 있는데, 용량 문제로 구글 포토 링크로 대체한다.
https://photos.app.goo.gl/cfgk6m9EXsqMihCb8
방에 소파도 있고, 킹 사이즈 침대도 있어 마음에 들었다.
하지만 그 무엇보다 좋았던 건 바로 호텔에서 볼 수 있는 뉴욕 뷰다.
뉴욕 야경
36층이라는 고층에 방을 잡아주어 뉴욕의 야경을 한눈에 볼 수 있었다.
호텔에서는 총, 약물 등 무섭게 느껴졌던 요소들로부터 안전하다는 생각이 들면서 이러한 야경을 보니 뉴욕에 온 게 실감 나면서 더욱 기대되었다.
멍청함
다음 날은 토요일이라 주말에 놀러 다닐 계획을 세워야 했다.
한국에서 나름 세워둔 것이 있어서 검토만 해보려 했는데, 생각지 못한 이유로 빨리 자야 했다.
열심히 충전기와 멀티탭까지 챙겨 왔는데 220v 짜리라 사용을 못했다...
분명 110v 쓰고 있는 거 알고 있고, 뉴욕이 처음인거지 미국이나 다른 110v 쓰는 나라들도 갔다 왔는데...
휴대폰 배터리도 없고 해서 빨리 자고 다음 날 어댑터 파는 곳이 있는지 돌아다녀 보기로 했다.
02024. 09. 13.

프로그래밍
논리적으로 생각하기 - Set 구현하기
우리가 프로그래밍을 할 때 많은 자료 구조를 활용하면서 알고있는 각 자료 구조의 연산별 시간 복잡도를 고려하여 코드를 작성한다.
이것만으로 충분히 논리적인 사고를 하고 있다고 할 수 있지만, 사고할 수 있는 영역과 배경 지식을 늘리기 위해서는 해당 자료 구조가 데이터를 어떻게 처리하는지를 추상적으로나마 파악할 수 있어야 한다.
이러한 논리적 사고력은 누구나 차근차근 생각해나가는 훈련만 한다면 익힐 수 있는 것으로, 한 번 논리적으로 사고할 수 있게 된다면 앞으로 겪게 되는 모든 경험을 성장의 밑거름으로 만들 수 있을 것이다.
요즘 IT에 최근에 올린 글이 바로 이러한 논리적 사고 과정을 보여주기 위한 글이다.
Set이 왜 필요한지의 목적을 세우는 것으로부터 시작하여,
가장 나이브한 접근에서부터 현재 많은 Set들이 구현되는 방식까지 어떻게 발전되었는지를 하나씩 살펴보았다.
이 글을 읽을 때에는 단계별로 마주치는 한계와 제한사항을 어떻게 해결해나갈 수 있는지를 생각하면서 읽어보자.
자연스럽게 확장성 있고 범용성 있는 자료 구조를 설계할 수 있는 능력을 갖출 수 있게 될 것이다.
https://yozm.wishket.com/magazine/detail/2723/
02024. 08. 23.

프로그래머스 > Java로 코테풀기
도넛과 막대 그래프 - Lv 2 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/258711?language=java
구현 중심의 문제로, 제시된 조건만 파악하면 쉽게 풀리는 문제였다.
문제에서 파악해야 하는 핵심 조건이 무엇이었는지를 알아보고, 이를 해결하기 위한 구현 과정을 살펴보자.
문제 풀이
문제에서는 도넛 묘양, 막대 모양, 8자 모양의 세 종류의 그래프를 제시합니다. 그리고 이 세 그래프에 속하지 않은 하나의 노드가 추가되어 모든 그래프를 연결합니다.
그래프 별 노드의 특징
먼저, 각 그래프에 속한 노드와 새로 추가한 노드의 특징을 살펴봅시다.
도넛 모양 그래프의 노드
도넛 모양 그래프의 모든 노드는 다음의 특징을 갖습니다.
하나의 나가는 간선과 하나의 들어오는 간선이 있습니다.
간선을 따라가다보면 자기 자신을 만나게 됩니다.
막대 모양 그래프의 노드
막대 그래프의 모든 노드는 다음의 특징을 갖습니다.
최대 하나의 나가는 간선과, 최대 하나의 들어오는 간선이 있습니다.
간선을 따라가다보면 막다른 노드에 도달합니다.
8자 모양 그래프의 노드
8자 모양 그래프의 모든 노드는 다음의 특징을 갖습니다.
하나의 들어오는 간선과 나가는 간선 또는 두 개의 들어오는 간선과 나가는 간선이 있습니다.
간선을 따라가다보면 두 개의 들어오는 간선과 나가는 간선을 갖는 노드를 만나게 됩니다.
새로 삽입된 노드
새로 삽입된 노드는 두 개 이상의 그래프를 연결하기 때문에 다음의 특징을 갖습니다.
들어오는 간선이 없습니다.
두 개 이상의 나가는 간선이 있습니다.
삽입된 노드 찾아 그래프 분리하기
위에서 살펴 본 노드의 특징을 활용하여 삽입된 노드를 찾아, 그래프들을 종류별로 분리할 수 있습니다.
삽입된 노드 찾기
새로 삽입된 노드의 특징 중 하나인 들어오는 간선이 없는 노드를 생각해 봅시다.
막대 모양 그래프의 시작 노드가 이러한 특징을 가질 수 있습니다. 그러나 나가는 간선이 두 개 이상이어야 한다는 점을 생각하면 이를 만족하는 노드는 새로 삽입된 노드 뿐입니다.
따라서 모든 노드를 순회하며, 들어오는 간선이 없고, 나가는 간선이 두 개 이상인 노드를 찾는다면, 해당 노드가 삽입된 노드임을 알 수 있습니다.
그래프 분리하기
삽입된 노드를 찾은 후에, 해당 노드와 연결된 간선들을 모두 끊으면 종류별로 명확히 분리된 그래프를 얻을 수 있습니다.
위 그림에서 알 수 있듯이, 삽입된 노드를 제거하면 왼쪽부터 8자 모양 그래프, 막대 모양 그래프, 8자 모양 그래프임을 쉽게 알 수 있습니다.
그래프 구분하기
그래프를 분리했으니 이제 각 그래프가 어떤 모양인지를 검사해야 합니다.
이 과정은 앞서 살펴본 노드의 특징을 활용하면 쉽게 할 수 있습니다.
임의의 한 노드로부터 출발하여 간선을 따라가다가,
막다른 노드에 도달한다면: 막대 모양 그래프
나가는 간선과 들어오는 간선의 수가 모두 2인 노드에 도달한다면: 8자 모양 그래프
출발 노드로 돌아온다면: 도넛 모양 그래프
여기서 주의할 점은, 8자 모양 그래프에 대한 검사를 도넛 모양 그래프 검사보다 우선 해야 한다는 것입니다.
8자 모양 그래프도 한 노드로부터 간선을 따라가다보면 자기 자신이 나오게 됩니다. 하지만 그 이전에 8자 모양 그래프의 중심 노드를 거쳐야 하기 때문에 이를 우선 검사하여 8자 모양 그래프와 도넛 모양 그래프를 구분합니다.
코드
이를 코드로 구현하면 다음과 같습니다.
import java.util.*;
import java.util.function.Function;
class Solution {
enum NodeType {
DONUT,
LINEAR,
EIGHT,
}
static class Node {
List<Node> outs = new ArrayList<>();
List<Node> ins = new ArrayList<>();
NodeType type;
}
private static Map<Integer, Node> constructNodes(int[][] edges) {
Map<Integer, Node> nodes = new HashMap<>();
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
if (!nodes.containsKey(u)) nodes.put(u, new Node());
if (!nodes.containsKey(v)) nodes.put(v, new Node());
Node from = nodes.get(u);
Node to = nodes.get(v);
from.outs.add(to);
to.ins.add(from);
}
return nodes;
}
private static int findInsertedNodeKey(Map<Integer, Node> nodes) {
for (int key : nodes.keySet()) {
Node node = nodes.get(key);
if (node.ins.size() == 0 && node.outs.size() >= 2) {
return key;
}
}
// Unreachable
return -1;
}
private static int removeInsertedNode(Map<Integer, Node> nodes) {
int insertedKey = findInsertedNodeKey(nodes);
Node inserted = nodes.remove(insertedKey);
for (Node node : inserted.ins) {
node.outs.remove(inserted);
}
for (Node node : inserted.outs) {
node.ins.remove(inserted);
}
return insertedKey;
}
private static Node getUnvisitedNext(Node node, List<Node> direction) {
for (Node next : direction) {
if (next.type == null) return next;
}
return null;
}
private static void mark(Node node, NodeType type, Function<Node, List<Node>> getDirection) {
do {
node.type = type;
node = getUnvisitedNext(node, getDirection.apply(node));
} while (node != null);
}
private static NodeType check(Node node) {
Node initial = node;
while (true) {
if (node.outs.size() == 0) {
mark(node, NodeType.LINEAR, n -> n.ins);
return NodeType.LINEAR;
} else if (node.ins.size() == 2 && node.outs.size() == 2) {
mark(getUnvisitedNext(node, node.outs), NodeType.EIGHT, n -> n.outs);
return NodeType.EIGHT;
}
node = getUnvisitedNext(node, node.outs);
if (node == null) {
// Unreachable
break;
}
if (node == initial) {
mark(node, NodeType.DONUT, n -> n.outs);
return NodeType.DONUT;
}
};
return null;
}
public int[] solution(int[][] edges) {
Map<Integer, Node> nodes = constructNodes(edges);
int insertedKey = removeInsertedNode(nodes);
int donut = 0;
int linear = 0;
int eight = 0;
for (Node node : nodes.values()) {
if (node.type != null) continue;
switch (check(node)) {
case LINEAR:
linear += 1;
break;
case EIGHT:
eight += 1;
break;
case DONUT:
donut += 1;
break;
}
}
return new int[] { insertedKey, donut, linear, eight };
}
}
02024. 08. 23.

Java
HashMap과 TreeMap은 언제 사용할까?
자바는 수많은 제네릭 컬렉션을 지원한다.
그 덕에 우리는 개발할 때 List, Stack, Map, Set 등을 간편하게 활용할 수 있다.
그런데 제네릭 컬렉션 중 많은 종류는 클래스가 아닌 인터페이스 형식으로 지원된다.
같은 자료 구조라고 하더라도 다른 방식으로 구현될 수 있기 때문이다.
가장 대표적인 자료 구조인 List 또한 ArrayList, LinkedList 등 여러 구현체가 있다.
이번 포스트에서 알아볼 Map 또한 HashMap과 TreeMap 등의 구현체들이 있다.
이러한 구현체들은 저마다 존재 이유가 있어서, 그 특징을 알고 상황에 맞게 사용할 수 있어야 한다.
그리고 그 특징을 알기 위한 가장 좋은 방법은 각 구현체가 어떻게 인터페이스를 구현하는지 이해하는 것이다.
이번 포스트에서는 Map 인터페이스를 구현하는 HashMap과 TreeMap이 Map의 기능들을 어떻게 구현하는지, 그리고 그 구현 방법에 의해 발생하는 특징은 무엇인지 살펴보자.
Map 인터페이스
Map의 구현체를 살펴보기 전, Map 자체에 대해 이해해 보도록 하자.
Map의 특징
Map은 다음과 같은 특징을 갖는다.
1. Key-Value 쌍
Map은 데이터를 key-value 쌍으로 저장하는 자료 구조이다. 각각의 값(value)은 고유한 키(key)를 통해 식별된다.
학생 정보를 저장하는 Map:
{
"홍길동": 95,
"김철수": 88,
"이영희": 92
}
위 예시에서 "홍길동", "김철수", "이영희"는 각각 학생 이름(key)을 나타내고, 95, 88, 92는 각 학생의 점수(value)를 나타낸다.
2. 유일한 Key
Map에서 각 키는 반드시 유일해야 한다. 동일한 키를 가진 데이터가 여러 개 존재할 수 없다. 만약 동일한 키로 새로운 값을 추가하면 기존 값은 새로운 값으로 덮어씌워진다.
기존 Map: { "홍길동": 95 }
새로운 값 추가: { "홍길동": 98 }
결과 Map: { "홍길동": 98 }
위 예시에서 "홍길동"의 키를 갖는 새로운 데이터를 추가함으로써, 기존에 있던 홍길동의 점수가 98로 변경되었다.
3. 순서가 특정되지 않음
Map은 저장되는 데이터의 순서를 보장하지 않는다. 데이터를 추가한 순서대로 값을 가져오거나 특정 위치의 값을 참조할 수 없다.
Map: { "홍길동": 95, "김철수": 88, "이영희": 92 }
위 Map에서 "홍길동", "김철수", "이영희" 순서로 값을 가져올 수 있다는 보장이 없다.
Map의 핵심 연산
Map의 구현체들은 위 특징들을 지키면서 다음의 연산을 지원해야 한다.
1. put(key, value)
put(key, value) 연산은 Map에 새로운 key-value 쌍을 추가하거나, 기존 키에 대한 값을 변경하는 데 사용된다.
새로운 key-value 쌍 추가: 만약 주어진 키가 Map에 존재하지 않으면, 새로운 key-value 쌍이 Map에 추가된다.
기존 값 변경: 만약 주어진 키가 이미 Map에 존재하면, 해당 키에 연결된 기존 값은 새로운 값으로 덮어씌워진다.
2. get(key)
get(key) 연산은 주어진 키에 해당하는 값을 Map에서 찾아 반환한다.
값 존재: 만약 주어진 키가 Map에 존재하면, 해당 키에 연결된 값이 반환된다.
값 미존재: 만약 주어진 키가 Map에 존재하지 않으면, null이 반환된다.
3. remove(key)
remove(key) 연산은 주어진 키에 해당하는 key-value 쌍을 Map에서 제거한다.
HashMap 클래스
HashMap은 **해시 테이블(Hash Table)**을 기반으로 동작하는 Map 인터페이스의 대표적인 구현체이다. 빠른 데이터 검색, 삽입, 삭제를 제공하며 다양한 활용 분야에서 사용된다.
구현 방식
해시 함수
HashMap은 해시 함수를 통해 데이트를 분류한다. 해시 함수는 데이터를 고정된 크기의 값으로 변환하는 함수이다. 이렇게 변환된 값을 해시 값(Hash Value) 또는 **해시 코드(Hash Code)**라고 한다.
해시 버킷
해시 함수로 얻은 해시 값을 인덱스로 사용하여, 데이터를 버킷(Bucket)이라는 배열에 저장한다.
충돌 해결
해시는 필연적으로 충돌이 발생한다. 즉, 서로 다른 두 데이터가 같은 해시 값을 뱉을 수 있다. 이를 해결하기 위해 각 버킷에 연결 리스트 (Linked List)를 두어 충돌된 데이터들을 관리한다.
시간 복잡도
데이터의 해시 값을 이용해 배열에 접근하므로 삽입, 검색, 삭제 연산 모두 O(1)의 시간 복잡도를 기대할 수 있다.
하지만 최악의 경우, 모든 데이터에 대해 해시 충돌이 발생하게 되면 모든 데이터가 연결 리스트로 관리되게 되어 O(n)의 시간 복잡도를 가진다.
사용하는 상황
HashMap은 모든 연산에 상수 시간을 기대할 수 있는 매우 빠른 자료 구조이다.
하지만 해시 충돌 시 빠른 연산의 장점이 사라지므로 데이터의 해시값 분포가 잘 되어있는지를 생각해야 한다.
TreeMap 클래스
TreeMap은 Map 인터페이스를 구현한 또 다른 자료 구조로, **균형 이진 탐색 트리(Red-Black Tree)**를 기반으로 동작한다.
균형 이진 탐색 트리
TreeMap은 데이터를 저장할 때 키를 기준으로 균형 이진 탐색 트리에 삽입한다. 이진 탐색 트리는 왼쪽 자식 노드의 키는 부모 노드의 키보다 작고, 오른쪽 자식 노드의 키는 부모 노드의 키보다 크거나 같은 특징을 가진다. 균형 이진 탐색 트리는 트리의 높이를 최소화하여 탐색, 삽입, 삭제 연산의 효율성을 높인다.
정렬된 Map
TreeMap은 키를 기준으로 정렬된 상태를 유지한다. 따라서 데이터를 추가한 순서와 상관없이 키의 순서대로 값을 가져올 수 있다. 이는 HashMap과 가장 큰 차이점 중 하나이다.
시간복잡도
평균적으로 O(log n)의 시간 복잡도를 가진다. 균형 이진 탐색 트리의 특성상 탐색, 삽입, 삭제 연산 시 트리의 높이만큼 비교 연산을 수행하기 때문이다.
이는 평균적으로 상수 시간의 시간 복잡도를 갖는 HashMap보다는 느리지만, TreeMap은 최악의 경우에도 O(log n)의 시간 복잡도를 보장한다.
사용하는 상황
TreeMap은 키를 기준으로 정렬된 상태를 유지하므로, 정렬 상태가 중요할 때 사용할 수 있다.
또, 이를 이용해 특정 범위 내의 키를 가진 데이터를 빠르게 찾을 수 있다.
결론
위 내용을 정리하면 다음과 같다.
따라서 다음의 기준에 따라 HashMap과 TreeMap 중 어떤 것을 사용할 지 결정할 수 있다.
HashMap을 사용하는 것이 좋은 경우
데이터의 순서가 중요하지 않은 경우
빠른 삽입, 삭제, 검색 속도가 중요한 경우
데이터의 규모가 크고 해시 충돌이 적을 것으로 예상되는 경우
TreeMap을 사용하는 것이 좋은 경우
데이터를 정렬된 상태로 유지해야 하는 경우
특정 범위 내의 키를 가진 데이터를 빠르게 찾아야 하는 경우 (범위 검색)
데이터의 순위 정보를 관리해야 하는 경우
02024. 07. 20.

Java
람다에서 로컬 변수 사용하기 - local variables referenced from a lambda expression must be final or effectively final
자바 코드를 작성하다보면 콜백을 사용해야 할 때가 있다.
콜백은 람다로 작성하는 일이 많은데, 이 때 다음과 같은 에러가 발생하는 경우가 있다.
java: local variables referenced from a lambda expression must be final or effectively final
이번 포스트에서는 이 에러가 나는 이유와 이를 해결할 수 있는 여러 방법들을 소개하고자 한다.
시나리오
에러를 재현하기 위해 다음과 같은 상황을 가정해보자.
긴 정수 배열에 대해 특정 작업을 반복해야 한다.
중간 중간 진행 상황을 알고자 한다.
이를 위한 메서드 runTasks()를 다음과 같이 작성했다고 하자.
private static void runTasks(int[] array, Consumer<Integer> onProgressUpdate) {
int tasksDone = 0;
for (int element : array) {
// 오래 걸리는 작업
task(element);
// 10개 작업이 끝날 때 마다 진행도 업데이트
if (++tasksDone % 10 == 0) {
onProgressUpdate.accept(tasksDone);
}
}
if (tasksDone % 10 != 0) {
onProgressUpdate.accept(tasksDone);
}
}
이 메서드를 호출할 때, 진행 상황을 다음과 같이 트래킹해보자.
public static void trackProgress() {
int currentProgress = 0;
runTasks(
new int[] {},
(progress) -> {
System.out.println("진행 상황: " + progress);
currentProgress = progress;
});
}
currentProgress = progress; 부분에서 문제의 에러가 발생함을 확인할 수 있다.
에러의 원인
에러 메세지를 보면 람다에서 참조하는 지역 변수는 final이거나 effectively final이어야 한다고 한다.
final 변수는 초기화 이후 값 변경이 불가능한 변수이며,
effectively final 변수는 final 키워드가 명시적으로 붙지는 않았지만 사실상 값이 변경되지 않는 변수를 의미한다.
위 예시에서는 currentProgress 변수가 람다 내부에서 값이 변경되기 때문에 문제가 발생하는 것이다.
왜 이러한 제약이 있는걸까?
람다에서 지역 변수의 변경이 제한되는 이유
람다에서 지역 변수의 값 변경이 제한되는 이유를 이해하기 위해 람다 표현식의 특성과 자바의 변수 스코프 개념을 되짚어보자.
람다는 자신을 둘러싼 외부 범위의 변수에 접근할 수 있다. (람다 캡처링, lambda capturing)
람다는 메서드 실행 종료 후에도 비동기적으로 실행될 수 있지만, 지역 변수는 메서드 실행이 종료되면 스택에서 사라진다.예를 들어, runTasks()에 전달된 람다를 클래스 멤버 변수로 저장해 놓았다고 생각해보자.
trackProgress() 메서드가 종료되는 시점에 currentProgress 변수는 스택에서 할당 해제된다.
반면, 전달된 onProgressUpdated 람다 객체는 여전히 살아있다.
이러한 문제를 해결하기 위해 자바는 람다 표현식이 캡처하는 지역 변수를 복사하여 별도의 공간에 저장하고, 람다 표현식은 복사된 값을 사용하도록 한다. 만약 원본 지역 변수의 값이 변경될 수 있다면 복사된 값과의 일관성이 깨져 오류가 발생할 수 있다.
따라서 람다 표현식 내부에서 사용되는 지역 변수는 final 또는 effectively final로 선언하여 값 변경을 방지해야 한다. 이를 통해 람다 표현식이 안전하게 변수에 접근하고 사용할 수 있도록 보장할 수 있다.
해결 방법
위에서 살펴보았듯, 람다에서 지역 변수를 직접 변경하는 것은 어렵다. 이를 해결할 수 있는 방법들에 대해 알아보자.
배열로 감싸기
currentProgress를 배열로 감싸는 것으로 이 문제를 우회할 수 있다. 자바에서 배열은 객체이므로, 람다 표현식 내부에서 배열의 요소 값을 변경하는 것은 허용된다.
private static void trackProgress() {
int[] currentProgress = {0}; // 배열로 감싸기
runTasks(
new int[] {},
(progress) -> {
System.out.println("진행 상황: " + progress);
currentProgress[0] = progress; // 배열 요소 변경
});
}
위 코드에서 currentProgress는 길이가 1인 정수 배열로 선언되었다. 람다 표현식 내부에서는 currentProgress[0]을 변경하여 진행 상황을 업데이트한다. 이렇게 하면 currentProgress 변수 자체는 변경되지 않고 배열의 요소 값만 변경되므로, effectively final 조건을 만족하게 된다.
이 방법은 가장 간단하게 문제를 해결할 수 있는 방법 중 하나이지만, 코드 가독성이 떨어지고 멀티 스레드 환경에서는 문제가 발생할 수 있다는 점을 유의해야 한다. 단일 스레드 환경에서 간단하게 문제를 해결하고 싶을 때 유용하게 사용할 수 있다.
장점
간단하고 빠르게 적용 가능: 코드를 크게 수정하지 않고도 문제를 해결할 수 있다.
기존 코드의 수정 최소화: 람다 표현식 외부의 코드를 거의 변경하지 않아도 된다.
단점
코드 가독성 저하: 배열을 사용하는 의도를 명확히 파악하기 어려워 코드 가독성이 떨어질 수 있다. 다른 개발자가 코드를 이해하기 어려울 수 있다.
멀티 스레드 환경에서 동기화 문제 발생 가능: 멀티 스레드 환경에서는 여러 스레드가 동시에 currentProgress[0] 값을 변경하려고 할 때 문제가 발생할 수 있다.
멤버 필드로 만들기
두 번째 해결 방법은 currentProgress 변수를 클래스의 멤버 필드로 선언하는 것이다. 멤버 필드는 람다 표현식의 외부에 선언되므로, 람다 표현식이 캡처하는 변수에 해당하지 않는다. 따라서 effectively final 조건의 적용 대상이 아니며, 람다 표현식 내부에서 자유롭게 값을 변경할 수 있다.
private static int currentProgress = 0; // 멤버 필드로 선언
private static void trackProgress() {
runTasks(
new int[] {},
(progress) -> {
System.out.println("진행 상황: " + progress);
currentProgress = progress; // 멤버 필드 변경
});
}
멤버 필드를 사용하는 방법은 람다 표현식 내부에서 변수에 직접 접근할 수 있어 코드가 간결해지고 가독성이 높아진다는 장점이 있다. 하지만 멀티 스레드 환경에서는 동기화 문제가 발생할 수 있으므로 주의해야 한다. 또한, 객체 지향 설계 원칙을 고려하여 신중하게 사용해야 한다.
장점
람다 표현식 내부에서 직접 접근 가능: 람다 표현식 내부에서 currentProgress 변수에 직접 접근하여 값을 변경할 수 있으므로, 코드가 더 간결해진다.
코드 가독성 향상: 배열을 사용하는 것보다 의도를 파악하기 쉽고, 코드 가독성이 높아진다.
단점
멀티 스레드 환경에서 동기화 문제 발생 가능: 멀티 스레드 환경에서는 여러 스레드가 동시에 currentProgress 값을 변경하려고 할 때 문제가 발생할 수 있다.
객체 지향 설계 원칙에 어긋날 수 있음: 멤버 필드를 사용하면 클래스의 상태가 외부에 노출될 수 있으며, 이는 객체 지향 설계 원칙에 어긋날 수 있다.
AtomicInteger 사용하기
세 번째 해결 방법은 AtomicInteger 클래스를 사용하여 currentProgress 변수를 선언하는 것이다. AtomicInteger는 멀티 스레드 환경에서 안전하게 정수 값을 변경할 수 있도록 설계된 클래스이다.
private static void trackProgress() {
AtomicInteger currentProgress = new AtomicInteger(0); // AtomicInteger 사용
runTasks(
new int[] {},
(progress) -> {
System.out.println("진행 상황: " + progress);
currentProgress.set(progress); // AtomicInteger 값 변경
});
}
위 코드에서 currentProgress는 AtomicInteger 객체로 선언되었다. 람다 표현식 내부에서는 currentProgress.set(progress) 메서드를 호출하여 진행 상황을 업데이트한다. AtomicInteger는 내부적으로 동기화 처리를 수행하므로, 멀티 스레드 환경에서도 안전하게 값을 변경할 수 있다.
이 방법은 멀티 스레드 환경에서 안전하게 값을 변경해야 하는 경우 가장 적합한 방법이다. Atomic 클래스의 다양한 기능을 활용하여 효율적인 코드를 작성할 수 있다. 단일 스레드 환경에서는 굳이 AtomicInteger를 사용할 필요는 없지만, 멀티 스레드 환경으로 확장될 가능성이 있다면 미리 AtomicInteger를 사용하는 것을 고려해 볼 수 있다.
또, 지역 변수로 선언할 수 있으므로 캡슐화 원칙도 지킬 수 있다.
장점
멀티 스레드 환경에서 안전하게 값 변경 가능: AtomicInteger는 멀티 스레드 환경에서 발생할 수 있는 경쟁 조건(race condition) 문제를 해결하여 안전하게 값을 변경할 수 있도록 보장한다.
Atomic 클래스의 다양한 기능 활용 가능: AtomicInteger는 getAndIncrement, getAndUpdate 등 다양한 메서드를 제공하여 원자적인 연산을 수행할 수 있도록 지원한다.
단점
Atomic 클래스 사용에 대한 이해 필요: AtomicInteger 클래스를 사용하려면 Atomic 클래스에 대한 기본적인 이해가 필요하다.
박싱/언박싱 오버헤드 발생 가능: AtomicInteger는 내부적으로 int 값을 객체로 감싸기 때문에, 박싱/언박싱 오버헤드가 발생할 수 있다. 하지만 대부분의 경우 성능에 큰 영향을 미치지 않는다.
마무리
지금까지 자바 람다 표현식에서 발생하는 "local variables referenced from a lambda expression must be final or effectively final" 에러의 원인과 해결 방법 세 가지를 살펴보았다.
람다 표현식은 자바 코드를 간결하고 효율적으로 작성하는 데 유용하지만, 외부 변수를 사용할 때 주의해야 할 점이 있다. 특히 람다 캡처링과 변수 범위를 이해하고, final 또는 effectively final 조건을 준수해야 한다.
이번 포스트에서 소개한 세 가지 해결 방법은 각각 장단점을 가지고 있으므로, 상황에 맞는 방법을 선택하여 적용하면 된다. 특히 멀티 스레드 환경에서는 AtomicInteger와 같은 Atomic 클래스들을 사용하는 것이 가장 안전하고 효율적인 방법이다.
이 글이 람다 표현식을 사용하는 데 어려움을 겪는 개발자들에게 도움이 되었기를 바란다.
02024. 07. 03.

Java
문자열 해시를 쓰면 안되는 이유 (HashMap, HashSet)
얼마 전, 아는 동생이 코테 대비 문제를 푸는데 똑같아야 할 것 같은 두 코드의 실행 시간이 너무 차이 난다는 이야기를 했다.
좌표를 다루어야 하는 문제인데, 한 코드는 다음과 같이 좌표를 int를 변환시켜 HashMap에 적용하였다.
Map<Integer, Integer> map = new HashMap<>();
while (/* 반복 */) {
int x = /* x 좌표 */;
int y = /* y 좌표 */;
int key = y * HEIGHT + x;
map.put(map.getOrDefault(key, 0) + 1);
}
또 다른 코드는 좌표를 String으로 변환하여 적용하였다.
Map<String, Integer> map = new HashMap<>();
while (/* 반복 */) {
int x = /* x 좌표 */;
int y = /* y 좌표 */;
String key = String.format("%d, %d", x, y);
map.put(map.getOrDefault(key, 0) + 1);
}
위 코드의 실행 시간은 0.3초, 아래 코드의 실행 시간은 1.8초로 어마어마한 성능 차이를 보였다.
어디서 이런 차이가 발생하는 걸까?
HashMap, HashSet 이해하기
많은 사람들이 HashMap이나 HashSet과 같이 해시라는 이름이 들어간 자료구조는 연산은 상수 시간 O(1)만에 한다고 생각하는 경향이 있다.
아니라는 것을 인지하고 있어도, 대부분 해시 충돌에 대해서만 신경쓴다.
하지만 HashMap과 HashSet을 사용할 때 가장 먼저 생각해 봐야 할 것은 해시 충돌이 아니다.
바로 키의 해시 코드를 어떻게 구하는 가이다.
이에 따라서 이 자료들에 대해서 알고 있는 시간 복잡도가 크게 바뀔 수 있기 때문이다.
연산 시간 복잡도
이 자료구조들은 내부적으로 키의 해시 코드를 이용하여 삽입, 삭제, 검색 등 연산을 수행한다.
이 연산들의 시간 복잡도는 일반적으로 O(1)을 기대할 수 있다.
문제는 해시 코드를 구할 때의 시간 복잡도이다.
해시를 활용하는 자료구조들은 자바의 Object 클래스에 선언된 hashCode() 메서드를 사용하여 해시를 구한다.
즉, hashCode()의 시간 복잡도가 이 자료구조들의 연산에 대한 시간 복잡도를 결정짓는 중요한 요소가 되는 것이다.
Integer::hashCode
위에서 첫 번째 코드는 키로 Integer를 사용하였다.
Integer의 hashCode()는 그 값 자체를 해시 값으로 사용할 수 있을 것 같다.
실제로 구글에 "java Integer implementation"이라고 검색하여 깃헙에 올라와있는 구현체를 살펴보면 다음과 같다.
https://github.com/openjdk/jdk/blob/master/src/java.base/share/classes/java/lang/String.java
@Override
public int hashCode() {
return Integer.hashCode(value);
}
public static int hashCode(int value) {
return value;
}
예상한 대로, 가지고 있는 값을 그대로 반환하여 상수 시간 안에 처리하게 된다.
이러한 경우 해시 충돌을 제외한다면 해시를 활용한 연산에 O(1)의 시간 복잡도를 기대할 수 있다.
String::hashCode
그렇다면 String의 시간 복잡도는 어떻게 될까?
직관적으로 생각해 보자.
문자열에 대한 해시 값을 생성하려면 문자열에 있는 모든 문자들을 순회하며 어떠한 처리를 해야 할 것 같다.
여기서부터 문자열의 hashCode()는 문자열의 길이 N에 비례하는 O(N)의 시간 복잡도가 걸릴 것 같다는 것을 의심할 수 있다.
구글에 "java String implementation"을 검색하여 이를 확인해 보자.
public int hashCode() {
int h = hash;
if (h == 0 && !hashIsZero) {
h = isLatin1() ? StringLatin1.hashCode(value)
: StringUTF16.hashCode(value);
if (h == 0) {
hashIsZero = true;
} else {
hash = h;
}
}
return h;
}
:: < String::hashCode 정의 > ::
라틴인지 여부에 따라 분기가 되어 다른 메서드로 해시 코드를 구한다.
더 일반적일 StringUTF16.hashCode()부터 쭉 따라가 보자.
public static int hashCode(byte[] value) {
return ArraysSupport.hashCodeOfUTF16(value, 0, value.length >> 1, 0);
}
:: < StringUtf16::hashCode 정의 > ::
public static int hashCodeOfUTF16(byte[] a, int fromIndex, int length, int initialValue) {
return switch (length) {
case 0 -> initialValue;
case 1 -> 31 * initialValue + JLA.getUTF16Char(a, fromIndex);
default -> vectorizedHashCode(a, fromIndex, length, initialValue, T_CHAR);
};
}
:: < ArraysSupport::hashCodeOfUTF16 정의 > ::
@IntrinsicCandidate
private static int vectorizedHashCode(Object array, int fromIndex, int length, int initialValue,
int basicType) {
return switch (basicType) {
case T_BOOLEAN -> unsignedHashCode(initialValue, (byte[]) array, fromIndex, length);
case T_CHAR -> array instanceof byte[]
? utf16hashCode(initialValue, (byte[]) array, fromIndex, length)
: hashCode(initialValue, (char[]) array, fromIndex, length);
case T_BYTE -> hashCode(initialValue, (byte[]) array, fromIndex, length);
case T_SHORT -> hashCode(initialValue, (short[]) array, fromIndex, length);
case T_INT -> hashCode(initialValue, (int[]) array, fromIndex, length);
default -> throw new IllegalArgumentException("unrecognized basic type: " + basicType);
};
}
:: < ArraysSupport::vectorizedHashCode 정의> ::
private static int utf16hashCode(int result, byte[] value, int fromIndex, int length) {
int end = fromIndex + length;
for (int i = fromIndex; i < end; i++) {
result = 31 * result + JLA.getUTF16Char(value, i);
}
return result;
}
:: < ArraysSupport::utf16hashCode 정의> ::
드디어 O(N)이 걸리는 부분이 등장했다.
utf16hashCode() 메서드는 fromIndex부터 fromIndex + length까지 반복을 돌며 O(length)만큼의 시간 복잡도를 갖는다.
처음부터 따라가 보면 이 length는 문자열의 길이가 되므로 String의 hashCode() 메서드는 O(N)이 걸리는 것을 실제로 확인할 수 있는 셈이다.
마무리
이렇게 해시 자료구조라고 하더라도 사용하는 자료형에 따라 상수 시간이 걸리지 않음을 확인할 수 있었다.
문제를 풀기 전 반드시 시간 복잡도를 계산하는 시간을 가져야 한다.
이때 해시를 구하는 시간 복잡도를 빼먹지 않도록 주의하자.
02024. 06. 26.

프로그래머스 > Java로 코테풀기
안티세포 - Lv 4 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/86054
프로그래머스에서는 가끔씩 월간 코드 챌린지라는 대회를 한다.
지금까지 총 3회를 했는데, 이 문제는 그 중 마지막인 월간 코드 챌린지 시즌 3에 출제된 문제이다.
DP인 것 같다는 생각이 들긴 했지만 조금 특이한 형태의 DP라 시간이 좀 걸렸다. 시간 복잡도를 활용해 풀이에 접근하는 방식을 한 번 살펴보도록 하자.
문제 풀이
입출력을 다루는 것은 따로 다루지 않고, 안티 세포 배열 b에 대해서 만들 수 있는 서로 다른 배열 c의 개수를 구하는 것만 다루겠습니다.
c를 구해야 할까? 문제 단순화 하기
이 문제의 핵심은 c를 과연 구해야 하는지 여부를 파악하는 데 있습니다.
예를 들어서, 문제에서 주어진 안티 세포인 (1)(1)(1)(1)이 있습니다.
이 안티 세포를 (1, 1)(1, 1)과 같은 형태로 합치는 c는 몇 개가 존재할까요?
[1, 3] 하나밖에 없습니다.
또, (1)(1)(1, 1)을 만들기 위한 c는 몇 개일까요?
[3] 하나입니다.
감이 오시나요?
안티 세포가 합쳐질 수 있는 모든 경우의 수에 대해서,
해당 경우의 수를 만들어낼 수 있는 c는 유일합니다.
반대로, 서로 다른 배열 c는 다르게 합쳐진 안티 세포 결과를 만들어 내게 됩니다.
이는 다음의 두 특성 때문에 성립하게 됩니다.
세포가 합쳐질 때, 두 세포는 같은 값을 가지고 있다.
b의 인덱스 i는 항상 증가하는 방향으로 이동한다.
이에 따라, 세포가 합쳐질 때, c에 기록되는 i는 합쳐지는 세포의 마지막 인덱스가 되게 됩니다.
즉 같은 형태의 합쳐진 세포를 만들기 위해서 해당 세포 내의 다른 인덱스가 기록되는 일이 없다는 뜻이고,
결과 모양이 같으면 c 또한 같다는 결론에 이르르게 됩니다.
이 내용을 파악했다면, 문제를 단순화할 수 있습니다.
이제 문제는 가능한 c의 개수를 구하는 것이 아니라, 안티 세포가 합쳐질 수 있는 경우의 수를 구하는 문제가 됩니다.
시간 복잡도로 해법 추정하기
문제에서 a의 길이가 최대 200,000이므로, b의 길이의 최대도 200,000이 됩니다.
b의 길이를 N이라고 합시다.
배열의 원소를 적어도 한 번씩은 방문해야 하기에, O(N)은 필연적으로 소요됩니다.
이제 원소를 방문할 때마다 얼마만큼의 시간 복잡도를 소요할 수 있는지를 생각해 봅시다.
N의 최대가 200,000인만큼 한 연산에 O(N)이 걸리게 된다면 전체 시간 복잡도가 O(N²)이 되어 시간 초과입니다.
한 번의 연산 당 가능한 시간 복잡도는 O(logN) 혹은 O(1)이 됩니다.
O(logN) 가능성 살펴보기
저번 포스트, 행렬과 연산 - Lv 4 문제 풀이에서 언급했듯이, O(logN)은 특별한 시간 복잡도입니다.
이 문제에 이를 적용할만한 내용이 있을까요?
행렬과 연산 문제와는 달리, 이번 문제에는 그런 내용이 있습니다.
바로 "같은 값을 가지고 있는 안티 세포만 합쳐질 수 있다"라는 점 때문입니다.
안티 세포가 여러 번 합쳐지는 경우를 생각해 봅시다.
처음엔 1 두 개가 합쳐져 2가 만들어집니다.
그 다음엔 2 두 개가 합쳐저 4가 만들어집니다.
그 다음엔 4 두 개가 합쳐저 8이 만들어집니다.
그 다음엔 8 두 개가 합쳐저 16이 만들어집니다.
이처럼 합쳐지는 안티 세포의 숫자는 계속 두 배씩 커지게 됩니다.
다음과 같은 배열을 생각해 봅시다.
[64, 32, 16, 8, 4, 2, 1, 1]
가장 오른쪽에 있는 1을 가능한 만큼 합치는 경우에 모든 원소가 합쳐집니다.
이는 O(N)번이라고 할 수 있을 것입니다.
그러면 연산에는 최대 O(N)이 걸리는 것이 아닐까요?
문제의 조건 중 원소의 값은 10^9보다 작거나 같다는 점이 있습니다.
안티 세포가 합쳐질 수 있는 가장 큰 수는 10^9인 것입니다.
그리고 이를 만들기 위해서는 최대 log_2(10^9)인 약 30번의 합 밖에 소요되지 않습니다.
즉, log는 배열의 길이에 적용되는 것이 아니라, 배열 원소의 값에 적용되는 것이었던 것을 알 수 있습니다.
10^9는 배열 b의 최댓값이므로 log_2(max(b))라고 표기할 수 있습니다.
따라서 전체 시간 복잡도는 O(n log(max(b))가 됩니다.
이는 n과 max(b)의 최댓값을 넣어보면 약 600만의 수치로 계산되어, 충분한 시간 복잡도입니다.
원소 당 연산 생각하기
위에서 log의 가능성을 확인하였습니다.
log가 배열 원소의 값에 적용이 된다는 것은, 해당 원소가 합쳐질 수 있는 횟수가 최대 log(max(b)) 번이라는 의미입니다.
연산의 시간 복잡도를 O(log(max(b))로 유지하기 위해서는 세포를 합쳐서 원하는 합을 만드는 경우의 수를 구하는 시간 복잡도는 상수 시간이어야 합니다. 그래야 이를 log(max(b)) 번 반복해도 전체 시간 복잡도가 O(log(max(b))가 되기 때문입니다.
즉, 각 원소 별로 만들 수 있는 합에 대해서, 각 경우의 수를 가지고 있어야 합니다.
예를 들어 [1, 1, 1, 1]의 경우에는 다음과 같은 데이터를 생성해낼 수 있어야 합니다.
b[0] = 1 b[1] = 1 b[2] = 1 b[3] = 1
합:1, 경우의 수: 1 합:1, 경우의 수: 1 합:1, 경우의 수: 2 합:1, 경우의 수: 3
합:2, 경우의 수: 1 합:2, 경우의 수: 1 합:2, 경우의 수: 2
합:4, 경우의 수: 1
경우의 수 구하기
각 합을 만들어내는 경우의 수를 구하기 위해, 우선 위의 표를 어떻게 만들 수 있는지 합 별로 하나씩 살펴봅시다.
1. 합 1을 만드는 경우
이 경우는 해당 원소만으로 안티 세포의 합을 만들어낼 수 있습니다.
따라서 직전 원소로 만들 수 있는 모든 경우의 수가 해당 원소로 합 1을 만드는 경우의 수가 됩니다.
예를 들어, 위 표에서 마지막 1로 합 1을 만드는 경우의 수를 구하기 위해서는 직전 1인 세 번째 1로 만들 수 있는 모든 경우의 수를 더해주면 됩니다.
2. 합 2를 만드는 경우
이 경우도 위와 비슷하게 처리할 수 있습니다.
합을 2를 만들기 위해선 직전 안티 세포와 합쳐야 합니다.
이 때 경우의 수는 합쳐진 안티 세포들을 제외하고, 그 앞에 있는 안티 세포로 만들 수 있는 경우의 수가 됩니다.
예를 들어, 마지막 1로 합 2를 만드는 경우의 수는 직전에 있는 1로 1을 만드는 경우의 수와 같습니다.
3. 합 4를 만드는 경우
합 4를 만들기 위해서는 합 2를 두 개 합쳐야 합니다.
따라서 이 경우의 수는 현재 검사하는 원소로 2를 만들 수 있는 경우의 수와,
이 안티 세포 직전의 원소를 포함해 2를 만들 수 있는 경우의 수를 곱한 것이 됩니다.
예를 들어, 마지막 1로 합 4를 만드는 경우는,
마지막 1로 합 2를 만드는 경우의 수인 1과
여기에 포함되지 않으면서, 직전 원소인 두 번째 1로 합 2를 만드는 경우의 수인 1을 곱하여
1이 그 경우의 수가 됩니다.
논리 일반화하기
여기까지 왔으면 합 2, 4를 만들어낸 논리를 다음과 같이 일반화 할 수 있습니다.
합 1을 만드는 경우의 수는 쉽게 구할 수 있으므로 제외합니다.
합 n을 만드는 경우의 수 =
해당 원소로 합 n/2를 만드는 경우의 수 *
안티 세포 직전 원소로 합 n/2를 만드는 경우의 수
합쳐진 안티 세포 직전 원소 구하기
해당 원소로 합 n/2를 만드는 경우의 수는 재귀적으로 쉽게 구할 수 있습니다.
그런데 안티 세포 직전 원소는 어떻게 구할 수 있을까요?
이를 구하기 위해서는 원소별로 합과 경우의 수 외에 안티 세포의 시작 인덱스를 함께 넣어주면 됩니다.
즉, 이제 다음과 같이 데이터를 만들어 주면 됩니다.
전체 코드
위 내용을 종합하면, 다음과 같이 문제를 풀 수 있습니다.
import java.util.*;
public class Solution {
private static final int DIV = 1_000_000_007;
private static int sum(int a, int b) {
long sum = (long) a + b;
return (int) (sum % DIV);
}
private static class Count {
final long sum;
final int count;
final int offset;
public Count(long sum, int count, int offset) {
this.sum = sum;
this.count = count;
this.offset = offset;
}
}
private int solve(int[] b) {
List<Map<Long, Count>> counts = new ArrayList<>(b.length);
for (int i = 0; i < b.length; i++) {
Map<Long, Count> map = new HashMap<>();
counts.add(map);
long targetSum = b[i];
if (i == 0) {
map.put(targetSum, new Count(targetSum, 1, i));
} else {
map.put(
targetSum,
new Count(
targetSum,
counts.get(i - 1).values().stream()
.mapToInt(c -> c.count)
.reduce(Solution::sum)
.orElse(0),
i));
}
while (true) {
targetSum *= 2;
Count lastCount = map.get(targetSum / 2);
int prevOffset = lastCount.offset - 1;
if (prevOffset < 0) break;
Map<Long, Count> prevMap = counts.get(prevOffset);
if (!prevMap.containsKey(targetSum / 2)) break;
Count count = prevMap.get(targetSum / 2);
map.put(targetSum, new Count(targetSum, count.count, count.offset));
}
}
return counts.get(counts.size() - 1).values().stream()
.mapToInt(c -> c.count)
.reduce(Solution::sum)
.orElse(0);
}
public int[] solution(int[] a, int[] s) {
int[] answer = new int[s.length];
int offset = 0;
for (int i = 0; i < answer.length; i++) {
answer[i] = solve(Arrays.copyOfRange(a, offset, offset + s[i]));
offset += s[i];
}
return answer;
}
}
02024. 06. 22.

프로그래머스 > Java로 코테풀기
행렬과 연산 - Lv 4 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/118670
정확성과 효율성 테스트가 같이 있는 문제이다.
코딩 테스트에서 이런 문제를 만나게 되면 효율성 테스트의 조건을 먼저 보아야 한다.
효율성 테스트를 해결할 수 있는 풀이는 정확성 테스트도 해결할 수 있지만,
정확성 테스트를 해결할 수 있는 풀이는 효율성 테스트를 통과하지 못할 수 있기 때문이다.
만약 처음부터 정확성 테스트의 조건을 해결하는 풀이를 고민한다면,
한 문제를 두 번 풀어야 하는 상황이 발생할 수 도 있다.
따라서 효율성 테스트를 먼저 고민하고, 정 모르겠다 싶으면 정확성 테스트의 조건을 보도록 하자.
이번 포스트에서는 효율성 테스트에 대한 풀이만 다루겠다.
문제 풀이
제한 사항으로 시간 복잡도 유추하기
문제의 제한 사항을 살펴봄으로써 문제가 원하는 해답의 시간 복잡도를 유추해 봅시다.
제한 사항에 따르면 행렬의 크기는 최대 100,000입니다. 이를 N이라고 합시다.
또, 연산의 개수도 최대 100,000입니다. 이를 M이라고 합시다.
만약 하나의 연산에 대해 행렬 전체를 업데이트 해야 한다면 연산 한 번에 O(N)의 시간 복잡도가 소요되어, 전체 시간 복잡도는 O(MN)이 됩니다.
이는 최대 100억에 해당하는 수치로, 시간 복잡도 제한인 1억을 훌쩍 넘겨버립니다.
operations를 순회하며 연산을 하나씩 적용하는 것은 줄일 수 없는 시간 복잡도입니다.
O(M)은 이미 정해져있고, 여기에 곱해지는 시간 복잡도인 연산 하나당 소요되는 시간 복잡도를 줄여야 한다는 의미입니다.
M 자체로 이미 10만이기 때문에 연산 하나 당 소요되는 시간 복잡도를 O(1), 혹은 적어도 O(logN)으로 줄여야 합니다.
연산에 대한 시간 복잡도 생각하기
O(logN)은 특별한 시간 복잡도입니다.
O(logN)이라는 시간 복잡도를 만들어 내는 접근법들은 대부분 그 유형이 정해져 있습니다.
트리, 이분 탐색, 분할 정복 등이 있는데, 이들 모두 배열을 회전시키는 연산과는 딱히 연결성이 없어 보입니다.
따라서 연산에 상수 시간인 O(1)이 소요되는 것이 가장 그럴듯합니다.
시간 복잡도 기반으로 연산 접근하기
연산에 상수 시간이 소요된다면 아주 간단한 연산으로 해결된다는 의미입니다.
ShiftRow의 경우 숫자가 섞이는 것이 아니기 때문에 행렬에서 가장 윗 행이 어디인지를 추적하는 것으로 상수 시간 안에 해결이 됩니다.
문제는 Rotate입니다. 숫자들의 순서가 바뀌게 되므로 실제 숫자들이 어떻게 움직이는지를 추적해야 합니다.
이를 어떻게 상수 시간 안에 해결할 수 있을까요?
Rotate 연산
문제에서 주어진 회전 연산을 생각해 보면, 행렬의 겉에서만 숫자들이 회전합니다.
즉, 가장자리를 상하좌우 4개로 나누어 생각해보면, 한쪽 가장자리에서 빠진 숫자는 다른 가장자리로 들어가게 됩니다.
이는 LinkedList로 해결할 수 있습니다.
행렬의 상하좌우를 관리하는 LinkedList를 만들어, 회전 연산 때 원소 하나를 제거하고 다른 리스트로 넣어주는 방식입니다.
LinkedList는 가장 앞 원소와 가장 뒤에 있는 원소의 추가/삭제 연산에 대한 시간 복잡도가 O(1)이므로 상수 시간 안에 해결할 수 있습니다.
rotate 연산을 실제로 상수 시간 안에 해결할 수 있게 된 것입니다.
그런데 이 LinkedList를 구성하는 방법에는 다음과 같이 여러 가지가 있습니다.
이 중 어떤 방식으로 리스트를 구성해야 할까요?
Rotate 연산만 생각하면 어떤 방식을 채택하든 큰 상관이 없습니다.
그렇다면 ShiftRow 연산까지 생각해 봅시다.
ShiftRow 연산
앞에서 배열의 행 인덱스를 이용해 상수 시간 안에 연산을 해결했는데,
Rotate 연산을 해결하려다 보니 배열의 실제 구성이 바뀌게 되었습니다.
ShiftRow 연산은 모든 숫자들을 한 칸씩 아래로 내립니다.
이를 쉽게 구현하기 위해서는 LinkedList가 열 방향으로, 즉 세로로 구성되어 있어야 합니다.
이렇게 구현해 놓게 되면 ShiftRow 연산이 발생했을 시에 가장 왼쪽과 오른쪽 LinkedList는 마지막 숫자를 빼서, 자신의 가장 앞에 넣어주면 됩니다.
가운데 남은 숫자들의 경우 ShiftRow 연산이 발생하면 가장자리로 갈 수 있게 됩니다.
따라서 Rotate 연산에 포함될 경우를 대비해 미리 다음과 같이 LinkedList에 넣어줍니다.
이제 ShiftRow 연산은 가운데에 있는 LinkedList 자체를 한 칸씩 내려주면 됩니다.
이를 위해 가운데 LinkedList 전체를 또 다른 LinkedList로 감싸줍니다.
ShiftRow와 Rotate 연산을 모두 상수 시간 안에 처리할 수 있기 때문에, 연산을 처리하는 시간 복잡도는 O(M)이 됩니다.
전체 시간 복잡도는 행렬의 원소를 한 번씩 읽고 쓰는 O(N)과 연산을 처리하는 O(M) 중 더 큰 시간 복잡도가 됩니다.
이는 O(N + M) 으로 표기할 수 있습니다.
LinkedList 구성 살펴보기
위에서 구성한 LinkedList를 이용하면 Rotate와 ShiftRow 연산을 상수 시간 안에 할 수 있습니다.
Rotate 연산에는 다음의 LinkedList들이 관여합니다.
ShiftRow 연산에는 다음의 LinkedList들이 관여합니다.
구현하기
Matrix 클래스 만들기
행렬에 관련된 연산을 처리하기 위한 클래스 Matrix를 다음과 같이 작성해 줍니다.
private static class Matrix {
public final int w;
public final int h;
Matrix(int[][] rc) {
w = rc[0].length;
h = rc.length;
}
}
LinkedList 구성하기
Matrix 클래스는 이차원 배열 rc를 생성자에 입력받아, 위에서 살펴본 LinkedList로 구성해주어야 합니다.
이를 위해 왼쪽 left, 오른쪽 right, 그리고 가운데의 LinkedList를 가리키는 body를 다음과 같이 선언해 줍니다.
private final LinkedList<Integer> left = new LinkedList<>();
private final LinkedList<Integer> right = new LinkedList<>();
private final LinkedList<LinkedList<Integer>> body = new LinkedList<>();
이 세 LinkedList들은 생성자에서 다음과 같이 채워줄 수 있습니다.
for (int i = 0; i < h; i++) {
LinkedList<Integer> bodyRow = new LinkedList<>();
for (int j = 0; j < w; j++) {
if (j == 0) {
left.add(rc[i][j]);
} else if (j == w - 1) {
right.add(rc[i][j]);
} else {
bodyRow.add(rc[i][j]);
}
}
body.add(bodyRow);
}
ShiftRow 연산
ShiftRow는 세 LinkedList의 가장 마지막 원소를 제거하고, 가장 앞 원소에 추가해 주는 연산을 해주는 연산입니다.
void shiftRow() {
left.addFirst(left.removeLast());
right.addFirst(right.removeLast());
body.addFirst(body.removeLast());
}
LinkedList의 addFirst(), removeLast() 연산은 상수 시간이므로, shiftRow() 메서드 또한 상수 시간이 걸림을 다시 한번 확인할 수 있습니다.
Rotate 연산
Rotate는 가장자리에 있는 LinkedList들끼리 원소를 하나씩 밀어주는 연산입니다.
void rotate() {
LinkedList<Integer> firstBodyRow = body.getFirst();
LinkedList<Integer> lastBodyRow = body.getLast();
firstBodyRow.addFirst(left.removeFirst());
lastBodyRow.addLast(right.removeLast());
right.addFirst(firstBodyRow.removeLast());
left.addLast(lastBodyRow.removeFirst());
}
마찬가지로 모든 메서드가 상수 시간을 가져, rotate() 연산 또한 상수 시간임을 확인할 수 있습니다.
여기에서 주의해야 할 점이, left, right에서 bodyRow들로 원소를 보내는 작업의 순서가 더 빨라야 한다는 점입니다.
bodyRow에서 left, right으로 원소를 보내는 작업을 먼저 해주게 된다면, 행렬의 가로길이가 2인 경우 bodyRow는 빈 LinkedList가 되는데, 이때 NoSuchElementException이 발생하게 됩니다.
이차원 배열 변환
마지막으로, 연산이 종료된 행렬을 다시 이차원 배열로 변환시켜주어야 합니다.
이는 build() 메서드에 다음과 같이 작성합니다.
int[][] build() {
int[][] matrix = new int[h][w];
Iterator<Integer> leftIterator = left.iterator();
Iterator<Integer> rightIterator = right.iterator();
Iterator<LinkedList<Integer>> bodyIterator = body.iterator();
for (int i = 0; i < h; i++) {
matrix[i][0] = leftIterator.next();
matrix[i][w - 1] = rightIterator.next();
Iterator<Integer> bodyRowIterator = bodyIterator.next().iterator();
for (int j = 1; j < w - 1; j++) {
matrix[i][j] = bodyRowIterator.next();
}
}
return matrix;
}
이 부분을 작성할 때, get()을 사용하여 LinkedList의 원소에 접근하지 않도록 주의해야 합니다.
LinkedList는 ArrayList와 달리, get()에 O(N)의 시간 복잡도가 소요되기 때문입니다.
어차피 LinkedList의 원소들을 순차적으로 접근하므로 Iterator를 이용하여 원소 참조에 불필요한 시간을 소요하지 않도록 합니다.
solution() 메서드
solution 메서드에서는 주어진 rc를 이용해 Matrix를 생성하고,
주어진 연산을 모두 적용해 준 다음,
이차원 배열로 변환하여 반환합니다.
public int[][] solution(int[][] rc, String[] operations) {
Matrix matrix = new Matrix(rc);
for (String operation : operations) {
switch (operation) {
case "ShiftRow":
matrix.shiftRow();
break;
case "Rotate":
matrix.rotate();
break;
}
}
return matrix.build();
}
전체 코드
import java.util.Iterator;
import java.util.LinkedList;
public class Solution {
private static class Matrix {
public final int w;
public final int h;
private final LinkedList<Integer> left = new LinkedList<>();
private final LinkedList<Integer> right = new LinkedList<>();
private final LinkedList<LinkedList<Integer>> body = new LinkedList<>();
Matrix(int[][] rc) {
w = rc[0].length;
h = rc.length;
for (int i = 0; i < h; i++) {
LinkedList<Integer> bodyRow = new LinkedList<>();
for (int j = 0; j < w; j++) {
if (j == 0) {
left.add(rc[i][j]);
} else if (j == w - 1) {
right.add(rc[i][j]);
} else {
bodyRow.add(rc[i][j]);
}
}
body.add(bodyRow);
}
}
void shiftRow() {
left.addFirst(left.removeLast());
right.addFirst(right.removeLast());
body.addFirst(body.removeLast());
}
void rotate() {
LinkedList<Integer> firstBodyRow = body.getFirst();
LinkedList<Integer> lastBodyRow = body.getLast();
firstBodyRow.addFirst(left.removeFirst());
lastBodyRow.addLast(right.removeLast());
right.addFirst(firstBodyRow.removeLast());
left.addLast(lastBodyRow.removeFirst());
}
int[][] build() {
int[][] matrix = new int[h][w];
Iterator<Integer> leftIterator = left.iterator();
Iterator<Integer> rightIterator = right.iterator();
Iterator<LinkedList<Integer>> bodyIterator = body.iterator();
for (int i = 0; i < h; i++) {
matrix[i][0] = leftIterator.next();
matrix[i][w - 1] = rightIterator.next();
Iterator<Integer> bodyRowIterator = bodyIterator.next().iterator();
for (int j = 1; j < w - 1; j++) {
matrix[i][j] = bodyRowIterator.next();
}
}
return matrix;
}
}
public int[][] solution(int[][] rc, String[] operations) {
Matrix matrix = new Matrix(rc);
for (String operation : operations) {
switch (operation) {
case "ShiftRow":
matrix.shiftRow();
break;
case "Rotate":
matrix.rotate();
break;
}
}
return matrix.build();
}
}
02024. 06. 20.

프로그래머스 > Java로 코테풀기
쌍둥이 빌딩 숲 - Lv 4 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/140105
처음 그림을 봤을 때 생긴 건 스택으로 푸는 히스토그램 문제랑 비슷하게 생겼다고 생각했다.
제목에 쌍둥이가 들어가서 짝을 찾아야 하나 하는 생각이 들어서 그런 것도 있는 것 같다.
하지만 문제를 읽어보니 전혀 스택과는 관련 없어보였다. 오히려 처음에 히스토그램 문제를 접했을 때 떠올리는 점화식을 활용한 재귀적 접근으로 풀리는 문제였다.
문제 풀이
같은 높이를 가지는 빌딩 사이에는 그보다 높은 빌딩이 존재하지 않습니다.
이 조건에 집중해 봅시다.
이것에 따르면 빌딩들이 배치된 상태에서 가장 작은 빌딩을 배치하려고 할 때,
가장 작은 빌딩의 쌍은 항상 붙어 있어야 한다는 것을 알 수 있습니다.
예를 들어, 다음과 같이 빌딩이 배치되어 있습니다.
가장 작은 노란색 빌딩 쌍을 추가한다고 생각해봅시다.
다음의 경우는 불가능합니다.
반면, 다음과 같이 노란색 빌딩 쌍을 붙인다면, 이미 있는 건물 사이에 어떤 곳에 배치하던 가능한 경우가 됩니다.
위의 그림에서 알 수 있는 중요한 점은 노란색 건물을 가장 앞에 배치하는 경우가 아니면, 노란색 건물은 보이지 않는다는 것입니다.
이를 활용하면 문제를 풀기 위한 점화식을 세울 수 있습니다.
다음과 같이 상태를 정의해봅시다.
(n, c): n개의 건물 쌍을 배치했을 때, c개의 건물이 보이는 경우의 수
- (0, 0) = 1
- (0, c) = 0
- (n, 0) = 0
- c > n인 경우 (n, c) = 0
n개의 건물 쌍을 배치 하기 위해서는:
n-1개의 건물 쌍을 배치
가장 작은 건물 쌍을 어디에 배치할 것인지 정하기
가장 작은 건물 쌍의 위치와 이 건물 쌍을 제외한 건물들의 배치가 다르기 때문에 중복이 발생하지 않습니다.
또, 가장 작은 건물은 어떤 경우이던 항상 존재하므로 누락이 발생하지도 않습니다.
가장 작은 건물을 맨 앞에 배치하는 경우:
1개의 경우의 수가 있습니다.
보이는 건물의 수가 1개 늘어납니다.
가장 작은 건물을 다른 건물 사이에 배치하는 경우:
2(n-1)개의 경우의 수가 있습니다.
보이는 건물의 수는 늘어나지 않습니다.
이를 이용하면, n개의 건물을 배치했을 때 c개의 건물이 보이기 위해서는, 이전 단계인 n-1개의 건물을 배치했을 때:
c-1개의 건물이 보이는 경우하나의 건물이 더 보여야 하므로 가장 작은 건물을 맨 앞에 배치
1개의 경우의 수
c개의 건물이 보이는 경우보이는 건물의 수가 늘어나지 않아야 하므로 다른 건물 사이에 배치
2(n-1)개의 경우의 수
즉, 다음과 같이 점화식을 쓸 수 있습니다.
(n, c) = (n-1, c-1) + (n-1, c) * 2(n-1)
시간 복잡도
하나의 상태를 계산할 때 별도의 반복이 필요하지 않습니다.
따라서 상태의 개수에 해당하는 시간 복잡도가 소요게 되어 O(nc)의 시간 복잡도를 갖습니다.
문제의 조건에 따라 n과 c의 최댓값은 100이므로 매우 넉넉한 시간 복잡도입니다.
최댓값 조건이 1000이어도 충분한 시간 복잡도가 됩니다.
전체 코드
import java.util.Arrays;
public class Solution {
private static final int DIV = 1_000_000_007;
private static final int[][] mem = new int[101][101];
static {
for (int[] row : mem) {
Arrays.fill(row, -1);
}
for (int n = 0; n <= 100; n++) {
mem[n][0] = 0;
for (int c = n + 1; c <= 100; c++) {
mem[n][c] = 0;
}
}
mem[0][0] = 1;
}
public int solution(int n, int count) {
if (mem[n][count] != -1) return mem[n][count];
long sum = solution(n - 1, count - 1);
sum += (long) solution(n - 1, count) * 2 * (n - 1);
return mem[n][count] = (int) (sum % DIV);
}
}
원래 static 블럭을 잘 사용하지 않는데, 이번 문제에서는 solution() 메서드 자체를 재귀시킬 수 있어서 사용했습니다.
02024. 06. 19.
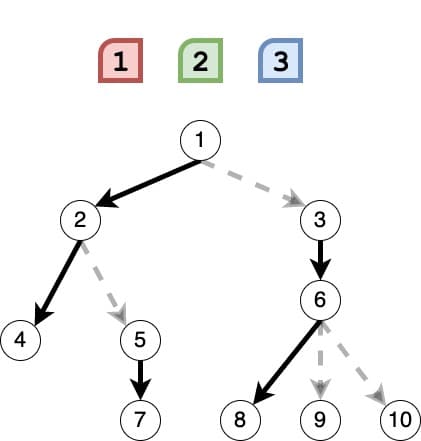
프로그래머스 > Java로 코테풀기
1, 2, 3 떨어뜨리기 - Lv. 4 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/150364
2023 카카오 블라인드의 문제이다.
트리 그림이 그려져 있지만 구현의 비중이 더 높았던 것 같다.
[취업과 이직을 위한 프로그래머스 문제 풀이 전략: 자바편]을 집필할 때 정말 신경 썼던 것이 가독성이다.
이 문제처럼 구현 비중이 높은 문제들을 특히 가독성을 생각하며 코드를 작성해야 한다.
" 읽기 쉬운 코드는 로직에만 집중할 수 있으므로 이해하기 쉽고, 실수가 있어도 쉽게 잡아낼 수 있습니다.
:: - [취업과 이직을 위한 프로그래머스 문제 풀이 전략: 자바편] 中 - ::
구현 문제의 풀이 코드는 문제에서 요구하는 로직을 다뤄야 한다.
로직이 제대로 구현되었는지를 파악하고, 실수를 줄이기 위해서는 가독성은 필수 요소이다.
문제 풀기
이 문제는 알고리즘적으로 설명할 것은 크게 없습니다. 풀이도 아주 직관적입니다.
문제의 조건을 만족하는 트리 구현
어떤 순서로 리프 노드들에 숫자가 떨어지는지 구하기
target을 만들 수 있는 방법이 있는지 검사하기
알고리즘보다는 구현에 초점이 맞춰진 문제인 만큼, 시간 복잡도를 따져보는 것은 의미가 없을 듯 하여 구현에 대한 내용만 다루겠습니다.
트리 구성하기
문제에서 edges가 이차원 배열로 주어지고, 이를 이용해 트리를 구성해야 합니다.
트리는 노드로 구성되어 있습니다.
가장 단순한 노드는 다음의 멤버 필드를 가지고 있을 것입니다.
index: 자신의 노드 번호.
children: 자식 노드들 리스트.
또, 다음의 메서드를 가집니다.
addChild(): 자식 노드 추가.
isLeaf(): 리프 노드인지 검사.
여기까지 코드
private static class Node {
public final int index;
private final List<Node> children = new ArrayList<>();
Node(int index) {
this.index = index;
}
void addChild(Node child) {
children.add(child);
}
void sortChild() {
children.sort(Comparator.comparingInt(n -> n.index));
}
private boolean isLeaf() {
return children.isEmpty();
}
}
이 문제의 노드는 조금 특별합니다.
여러 자식 노드들 중 하나의 자식만 참조할 수 있고,
한 번 참조한 이후에는 다음 자식 노드를 참조하게 됩니다.
또, 이 순서는 자식 노드의 index 순서를 따릅니다.
이에 따라 다음의 메서드를 정의합니다.
trigger(): 연결된 노드를 따라 내려갔을 때 도착하는 리프 노드를 반환. 한 번 호출 후에는 다음 자식 노드를 참조.
sortChild(): 등록된 자식 노드들을 index 순으로 정렬.
이 부분에 해당하는 코드
private int childIndex = 0;
Node trigger() {
if (isLeaf()) {
return this;
}
Node leaf = children.get(childIndex).trigger();
childIndex = (childIndex + 1) % children.size();
return leaf;
}
void sortChild() {
children.sort(Comparator.comparingInt(n -> n.index));
}
완성된 Node 클래스는 다음과 같습니다.
private static class Node {
public final int index;
private final List<Node> children = new ArrayList<>();
private int childIndex = 0;
Node(int index) {
this.index = index;
}
Node trigger() {
if (isLeaf()) {
return this;
}
Node leaf = children.get(childIndex).trigger();
childIndex = (childIndex + 1) % children.size();
return leaf;
}
void addChild(Node child) {
children.add(child);
}
void sortChild() {
children.sort(Comparator.comparingInt(n -> n.index));
}
private boolean isLeaf() {
return children.isEmpty();
}
}
문제에서 입력 받은 edges를 이용하여 Node로 구성된 트리를 만들어 주는 constructTree() 메서드를 다음과 같이 정의해 줍니다.
private static Node constructTree(int[][] edges) {
Node[] nodes = new Node[edges.length + 1];
for (int i = 0; i < nodes.length; i++) {
nodes[i] = new Node(i);
}
for (int[] edge : edges) {
nodes[edge[0] - 1].addChild(nodes[edge[1] - 1]);
}
for (Node node : nodes) {
if (node == null) continue;
node.sortChild();
}
return nodes[0];
}
이렇게 구성된 트리를 이용하면 숫자가 떨어지는 리프 노드의 순서를 구할 수 있습니다.
target 숫자를 만들 수 있는지 검사
리프 노드에 떨어지는 횟수가 너무 적거나 너무 많다면 해당 리프 노드에서 원하는 숫자를 만들 수 없습니다.
이를 관리하기 위해 노드별로 목표하는 target 숫자를 만드는 클래스 Target을 만들어줍니다.
Target 클래스는 다음과 같은 멤버 필드를 가지게 됩니다.
value: 해당 노드의 target 숫자
tries: 해당 노드에 숫자가 떨어진 횟수
이 두 값을 이용하면 다음의 연산을 할 수 있습니다.
addTry(): 해당 노드에 숫자가 떨어진 횟수 1 증가
isNotEnough(): 아직 target 숫자를 만들기에는 해당 노드에 숫자가 떨어진 횟수가 부족
떨어진 횟수 x 3이 해당 횟수로 만들 수 있는 최대 숫자
didTooManyTries(): target 숫자를 만들기에는 해당 노드에 숫자가 너무 많이 떨어짐
떨어진 횟수 자체가 해당 횟수로 만들 수 있는 최소 숫자
isSolved(): target 숫자를 만들 수 있을 만큼 해당 노드에 숫자가 떨어짐
여기까지 코드
private static class Target {
public final int value;
private int tries = 0;
Target(int value) {
this.value = value;
}
void addTry() {
tries += 1;
}
boolean isNotEnough() {
return value > tries * 3;
}
boolean didTooManyTries() {
return value < tries;
}
boolean isSolved() {
return !isNotEnough() && !didTooManyTries();
}
}
target 숫자를 만들기 위해 떨어뜨려야 하는 숫자 순서 구하기
위의 Target 클래스를 이용해서 각 노드별로 숫자를 떨어뜨리는 횟수를 구할 수 있었습니다.
이 횟수를 이용해 이 노드에 숫자를 어떤 순서로 떨어뜨려야 하는지를 구해 봅시다.
사전 순으로 가장 앞선 숫자들을 구해야 하므로, 3을 최대한 많이 사용하고, 그 다음으로 2를 최대한 사용해야 합니다.
그렇게 함으로써 1을 사용하는 빈도가 늘어나고, 사전순으로 앞서게 됩니다.
예를 들어, 숫자 4개를 이용하여 9을 구성해야 하는 경우를 생각해 봅시다.
2-2-2-3, 1-2-3-3 등 여러 조합이 나올 수 있습니다.
하지만 이 중 가장 사전 순으로 앞선 것은 3을 가장 많이 사용한 1-2-3-3입니다.
이 로직을 구현해 봅시다.
숫자를 떨어뜨릴 때에는 최소 1씩은 떨어뜨려야 합니다.
따라서 1은 각 떨어뜨리는 시도 당 미리 깔아 두고, 나머지 숫자를 분배합니다.
예를 들어, 위와 같이 4번의 시도로 9를 만든다면, 4번 각각의 시도에 미리 다음과 같이 1을 깔아 둡니다.
:: 1-1-1-1 ::
이제 남은 숫자인 5를 분배하면 됩니다.
이미 1을 모두 깔아 두었기 때문에 3을 최대한 많이 사용하기 위해서는 남은 숫자를 2로 나누어 그 몫을 계산합니다.
2를 최대한 많이 분배하여 3을 만들어야 하기 때문입니다. 같은 이유로, 2로 나눈 나머지는 2를 사용하는 횟수가 됩니다.
숫자를 떨어뜨리는 시도 당 1씩 깔아 두고, 나머지 숫자 remainder 구하기
remainder를 2로 나눈 몫이 숫자 3을 떨어뜨리는 횟수
remainder를 2로 나눈 나머지가 숫자 2를 떨어뜨리는 횟수
남은 시도들은 모두 숫자 1을 떨어뜨리는 횟수
여기에 해당하는 코드
int[] count = new int[3];
int remainders = value - tries;
count[2] = remainders / 2; // 숫자 3을 떨어뜨리는 횟수
count[1] = remainders % 2; // 숫자 2를 떨어뜨리는 횟수
count[0] = tries - count[1] - count[2]; // 숫자 1을 떨어뜨리는 횟수
이제 이 숫자들을 나열해 주어야 합니다.
배열로 만들 수도 있고, 리스트로 만들 수도 있을 텐데, 결정을 내리기 위해 이것들이 나중에 어떻게 사용될지를 생각해 봅시다.
각 리프 노드 별로 Target 클래스를 만들었고, 리프 노드를 방문하는 순서도 알고 있습니다.
또, 리프 노드 별로 사용되어야 하는 숫자들의 순서도 알고 있죠.
리프 노드를 방문하는 순서를 따라가면서, 사용되어야 하는 숫자들을 하나씩 사용하면 됩니다.
즉, 선입선출을 갖는 자료 구조인 큐를 사용하는 것이 적합해 보입니다.
위에서 구현한 로직을 이용해 큐를 구성하여 반환하는 solve() 메서드를 작성해 줍니다.
Queue<Integer> solve() {
int[] count = new int[3];
int remainders = value - tries;
count[2] = remainders / 2;
count[1] = remainders % 2;
count[0] = tries - count[1] - count[2];
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < count.length; i++) {
for (int j = 0; j < count[i]; j++) {
q.add(i + 1);
}
}
return q;
}
solution 메서드
마지막으로 이 모든 단계를 조합하여 문제를 해결해 줍니다.
private static boolean checkAll(Target[] targets, Function<Target, Boolean> map) {
for (Target t : targets) {
if (t.value == 0) continue;
if (!map.apply(t)) {
return false;
}
}
return true;
}
public int[] solution(int[][] edges, int[] target) {
Node tree = constructTree(edges);
List<Integer> leaves = new ArrayList<>();
Target[] targets = Arrays.stream(target).mapToObj(Target::new).toArray(Target[]::new);
do {
int leaf = tree.trigger().index;
leaves.add(leaf);
targets[leaf].addTry();
if (checkAll(targets, Target::didTooManyTries)) {
return new int[] {-1};
}
} while (!checkAll(targets, Target::isSolved));
List<Queue<Integer>> queues = Arrays.stream(targets).map(Target::solve).collect(Collectors.toList());
return leaves.stream().mapToInt(leaf -> queues.get(leaf).poll()).toArray();
전체 코드
import java.util.*;
import java.util.function.Function;
import java.util.stream.Collectors;
public class Solution {
private static class Node {
public final int index;
private final List<Node> children = new ArrayList<>();
private int childIndex = 0;
Node(int index) {
this.index = index;
}
Node trigger() {
if (isLeaf()) {
return this;
}
Node leaf = children.get(childIndex).trigger();
childIndex = (childIndex + 1) % children.size();
return leaf;
}
void addChild(Node child) {
children.add(child);
}
void sortChild() {
children.sort(Comparator.comparingInt(n -> n.index));
}
private boolean isLeaf() {
return children.isEmpty();
}
}
private static class Target {
public final int value;
private int tries = 0;
Target(int value) {
this.value = value;
}
void addTry() {
tries += 1;
}
boolean isNotEnough() {
return value > tries * 3;
}
boolean didTooManyTries() {
return value < tries;
}
boolean isSolved() {
return !isNotEnough() && !didTooManyTries();
}
Queue<Integer> solve() {
int[] count = new int[3];
int remainders = value - tries;
count[2] = remainders / 2;
count[1] = remainders % 2;
count[0] = tries - count[1] - count[2];
Queue<Integer> q = new LinkedList<>();
for (int i = 0; i < count.length; i++) {
for (int j = 0; j < count[i]; j++) {
q.add(i + 1);
}
}
return q;
}
}
private static Node constructTree(int[][] edges) {
Node[] nodes = new Node[edges.length + 1];
for (int i = 0; i < nodes.length; i++) {
nodes[i] = new Node(i);
}
for (int[] edge : edges) {
nodes[edge[0] - 1].addChild(nodes[edge[1] - 1]);
}
for (Node node : nodes) {
if (node == null) continue;
node.sortChild();
}
return nodes[0];
}
private static boolean checkAll(Target[] targets, Function<Target, Boolean> map) {
for (Target t : targets) {
if (t.value == 0) continue;
if (!map.apply(t)) {
return false;
}
}
return true;
}
public int[] solution(int[][] edges, int[] target) {
Node tree = constructTree(edges);
List<Integer> leaves = new ArrayList<>();
Target[] targets = Arrays.stream(target).mapToObj(Target::new).toArray(Target[]::new);
do {
int leaf = tree.trigger().index;
leaves.add(leaf);
targets[leaf].addTry();
if (checkAll(targets, Target::didTooManyTries)) {
return new int[] {-1};
}
} while (!checkAll(targets, Target::isSolved));
List<Queue<Integer>> queues = Arrays.stream(targets).map(Target::solve).collect(Collectors.toList());
return leaves.stream().mapToInt(leaf -> queues.get(leaf).poll()).toArray();
}
}
02024. 06. 17.

프로그래머스 > Java로 코테풀기
경사로의 개수 - Lv. 4 문제 풀이
https://school.programmers.co.kr/learn/courses/30/lessons/214290
2023년 현대 모비스 알고리즘 경진대회 예선 문제라고 한다.
현대 모비스에서 소프트웨어를 강조하기 위해 주최하는 경진대회라고 하는데 어마어마한 상품으로 상당히 화제였었다.
1위 상이 무려 아이오닉 5... 차 한대가 상품이었다.
2등상은 1,000만원 3등상은 500만원으로 역대급 대회였다.
하지만 그런 만큼 진짜 쟁쟁하신 분들이 나오셨다고...
2024년 현대 모비스 알고리즘 경진대회도 총 상금 1억 7천만원이 걸려 있고, 프로그래머스에서 6월 25일까지 접수받고 있다.
=> 2024년 현대 모비스 알고리즘 경진대회 접수
어쨌든 이 문제는 프로그래머스에서 Lv4로 등재되었고, 2차원 배열과 이동 가능한 조건이 주어졌을 때, 이동 가능한 경로의 개수를 찾는 문제이다.
문제 풀기
제한 사항으로 접근법 떠올려보기
문제에서 주어진 제한 사항은 다음과 같습니다.
3 ≤ grid의 길이 = n ≤ 8
3 ≤ grid[i]의 길이 = m ≤ 8
0 ≤ grid[i][j] ≤ 1,000
1 ≤ d의 길이 ≤ 100
1 ≤ k ≤ 10^9
그리드의 크기는 작은 반면, k의 크기는 10억으로 매우 크다는 것을 알 수 있습니다.
k는 d를 반복해야 하는 횟수이므로 k번에 해당하는 만큼 반복을 해야 할 것 같기는 한데, 그 값을 보니 k번 반복을 해서는 안됩니다.
그렇다면 log의 시간 복잡도를 가지는 분할 정복을 떠올릴 수 있습니다.
k를 반으로 나눠가며 연산하는 분할 정복이라면 O(logK)번 만에 k번에 해당하는 반복을 계산해낼 수 있을 것입니다.
이제 문제를 분할 정복에 맞도록 정의할 수 있는지를 확인하면 됩니다.
부분 문제 정의하기
주어진 문제를 분할 정복을 활용해 k번 반복되는 부분 문제로 만들어야 합니다.
문제에서 k번 반복되는 것은 d를 적용하는 횟수입니다.
따라서 d를 적용하는 횟수의 가장 최소 횟수인 1인 문제를 먼저 풀고, 이를 k번 반복하는 것으로 접근할 수 있습니다.
(x1, y1, x2, y2): (x1, y1)에서 (x2, y2)로 d를 이용하여 이동하는 경로의 수
(x1, y1, x2, y2)는 제 책 [취업과 이직을 위한 프로그래머스 코딩 테스트 문제 풀이 전략: 자바편]에서 소개한 문제를 나타내기 위한 표기법으로, 문제를 정의하기 위해 필요한 변수의 집합이라고 생각하시면 됩니다.
더 작은 부분 문제
그런데 위의 문제를 풀기 위해서는 경로를 파악해야 합니다.
이는 다시 부분 문제를 정의하여 다음과 같이 재귀적으로 해결할 수 있습니다.
(x1, y1, x2, y2, di): (x1, y1)에서 (x2, y2)로 d[di]~d[끝]을 이용해서 갈 수 있는 경우의 수 \
= (x1, y1, x, y, i) * (x, y, x2, y2, d.length - i) => 모든 x, y와 di <= i <= d.length에 대한 반복 합
(x1, y1, x2, y2, di)를 풀면, (x1, y1, x2, y2) = (x1, y1, x2, y2, 0)으로 구할 수 있게 됩니다.
이 부분에 해당하는 코드
private static final int DIV = 1_000_000_007;
private static final int[] dx = {1, 0, -1, 0};
private static final int[] dy = {0, 1, 0, -1};
private static int count(
int x1, int y1, int x2, int y2, int di, int[][] grid, int[] d, int[][][][][] mem) {
// Memoization
if (mem[di][x1][y1][x2][y2] != -1) {
return mem[di][x1][y1][x2][y2];
}
// 종료 조건
if (di == d.length) {
if (x1 == x2 && y1 == y2) {
return mem[di][x1][y1][x2][y2] = 1;
} else {
return mem[di][x1][y1][x2][y2] = 0;
}
}
// 재귀
int sum = 0;
for (int i = 0; i < 4; i++) {
int nx = x1 + dx[i];
int ny = y1 + dy[i];
try {
if (grid[ny][nx] == grid[y1][x1] + d[di]) {
sum += count(nx, ny, x2, y2, di + 1, grid, d, mem);
sum %= DIV;
}
} catch (IndexOutOfBoundsException ignored) {
}
}
return sum;
}
private static int[][][][] buildCountMatrix(int[][] grid, int[] d) {
int w = grid[0].length;
int h = grid.length;
// [i][x1][y1][x2][y2]: (x1, y1) -> (x2, y2)를 d[i] ~ d[끝]을 이용해 갈 수 있는 경우의 수
int[][][][][] mem = new int[d.length + 1][w][h][w][h];
for (int di = d.length; di >= 0; di--) {
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
Arrays.fill(mem[di][x1][y1][x2], -1);
for (int y2 = 0; y2 < h; y2++) {
mem[di][x1][y1][x2][y2] = count(x1, y1, x2, y2, di, grid, d, mem);
}
}
}
}
}
return mem[0];
}
부분 문제 시간 복잡도
(x1, y1, x2, y2, di)의 경우 재귀가 진행됨에 따라 반복되는 부분 문제이기 때문에 한 단계의 상태를 구하기 위한 시간 복잡도와 상태의 개수를 이용해 시간 복잡도를 계산할 수 있습니다.
하나의 상태를 구하기 위해서는 d의 길이만큼 반복하고, x, y에 대해서도 반복합니다.
1 <= d의 길이 <= 100
3 <= x, y, <= m = 8
주어진 조건이 위와 같으므로시간 복잡도는 **O(dm²)**이 되고, 최댓값을 대입했을 때 6,400이므로 이 부분 문제는 충분한 시간 복잡도를 가지고 있음을 알 수 있습니다.
분할 정복
(x1, y1, x2, y2)를 해결할 수 있으니, 이를 이용해 k번 반복하는 문제를 해결해야 합니다.
이 문제는 다음과 같이 정의할 수 있습니다.
(x1, y1, x2, y2, r): (x1, y1)에서 (x2, y2)로 d를 r번 이용하여 이동하는 경우의 수
= (x1, y1, x, y, r / 2) * (x, y, x2, y2, r / 2) => r이 짝수일 경우
= (x1, y1, x, y, r / 2) * (x, y, x2, y2, r / 2) * (x1, y1, x2, y2, 1) => r이 홀수일 경우
(x1, y1, x2, y2, 1) = (x1, y1, x2, y2)
모든 x1, y1, x2, y2에 대해 이를 반복한다면 답을 구할 수 있습니다.
그런데 문제가 있습니다. 이 부분 문제는 메모이제이션을 적용할 수 없다는 것입니다.
r의 크기는 최대 10억으로, 이는 메모이즈하기에는 너무 큰 값입니다.
모든 출발점과 도착점에 대해서 같은 연산을 해야 한다는 점을 생각하면 비슷하지만 조금 다른 접근 방식을 생각할 수 있습니다.
행렬 연산
한 점에서 다른 점으로 이동하는 경로의 수는 행렬로 표현할 수 있습니다.
사실, 이미 행렬로 표현되어 있습니다.
문제 (x1, y1, x2, y2)가 풀어낸 답이 바로 그 행렬입니다.
이 문제의 결과는 [x1, y1, x2, y2]의 4차원 배열이 됩니다.
이 배열의 각 원소는 (x1, y1)에서 (x2, y2)로 이동할 수 있는 경로의 수를 가지고 있습니다.
지금 우리가 구해야 하는 것은 (x1, y1)에서 출발하고, (x2, y2)에 도착하지만, 그 과정 중에 어떠한 좌표 (x, y)를 경유하면서 이동하는 경우의 수입니다.
이는 행렬의 곱셈과 같습니다. 즉, 행렬을 k번 거듭제곱하는 것으로 모든 좌표에 대해 같은 연산을 적용할 수 있게 됩니다.
이 부분에 해당하는 코드
private int[][][][] multiply(int[][][][] a, int[][][][] b) {
int w = a.length;
int h = a[0].length;
int[][][][] m = new int[w][h][w][h];
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
for (int y2 = 0; y2 < h; y2++) {
for (int x = 0; x < w; x++) {
for (int y = 0; y < h; y++) {
m[x1][y1][x2][y2] += (int) (((long) a[x1][y1][x][y] * b[x][y][x2][y2]) % DIV);
m[x1][y1][x2][y2] %= DIV;
}
}
}
}
}
}
return m;
}
private int[][][][] power(int[][][][] matrix, int power) {
if (power == 1) {
return matrix;
}
if (power == 2) {
return multiply(matrix, matrix);
}
int[][][][] result = power(power(matrix, power / 2), 2);
if (power % 2 == 1) {
result = multiply(result, matrix);
}
return result;
}
행렬 연산 시간 복잡도
한 번의 재귀 단계에 x1, y1, x2, y2, x, y에 대해서 반복합니다.
반복의 깊이는 log k이므로 전체 시간 복잡도는 **O(log k * m^6)**이 됩니다.
마무리
이제 결과 행렬에서 모든 원소를 순회하며 경로의 개수 합을 구해주면 됩니다.
이 부분에 해당하는 코드
public int solution(int[][] grid, int[] d, int k) {
int[][][][] matrix = buildCountMatrix(grid, d);
matrix = power(matrix, k);
int count = 0;
int w = matrix.length;
int h = matrix[0].length;
//noinspection ForLoopReplaceableByForEach Suppress for better readability.
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
for (int y2 = 0; y2 < h; y2++) {
count += matrix[x1][y1][x2][y2] % DIV;
count %= DIV;
}
}
}
}
return count;
}
전체 시간 복잡도
전체 풀이는 다음의 단계를 따라갑니다.
(x1, y1, x2, y2, di)를 해결하는 부분시간 복잡도: O(dm²)
행렬의 거듭제곱을 계산하는 부분시간 복잡도: O(log k * m^6)
경로 합을 구하는 부분시간 복잡도: O(m⁴)
따라서 전체 시간 복잡도는 O(dm²) + O(log k * m^6) + O(m⁴) = O((d + log k * m⁴)m²)이 되고,
최댓값을 고려했을 때 d < log k * m⁴d이므로 **O(log k * m^6)**이 됩니다.
제한 사항을 고려해 최댓값을 대입하면 약 784만이라는 값이 나와, 충분한 시간 복잡도라는 것을 알 수 있습니다.
전체 코드
import java.util.Arrays;
public class Solution {
private static final int DIV = 1_000_000_007;
private static final int[] dx = {1, 0, -1, 0};
private static final int[] dy = {0, 1, 0, -1};
private static int count(
int x1, int y1, int x2, int y2, int di, int[][] grid, int[] d, int[][][][][] mem) {
// Memoization
if (mem[di][x1][y1][x2][y2] != -1) {
return mem[di][x1][y1][x2][y2];
}
// 종료 조건
if (di == d.length) {
if (x1 == x2 && y1 == y2) {
return mem[di][x1][y1][x2][y2] = 1;
} else {
return mem[di][x1][y1][x2][y2] = 0;
}
}
// 재귀
int sum = 0;
for (int i = 0; i < 4; i++) {
int nx = x1 + dx[i];
int ny = y1 + dy[i];
try {
if (grid[ny][nx] == grid[y1][x1] + d[di]) {
sum += count(nx, ny, x2, y2, di + 1, grid, d, mem);
sum %= DIV;
}
} catch (IndexOutOfBoundsException ignored) {
}
}
return sum;
}
private static int[][][][] buildCountMatrix(int[][] grid, int[] d) {
int w = grid[0].length;
int h = grid.length;
// [i][x1][y1][x2][y2]: (x1, y1) -> (x2, y2)를 d[i] ~ d[끝]을 이용해 갈 수 있는 경우의 수
int[][][][][] mem = new int[d.length + 1][w][h][w][h];
for (int di = d.length; di >= 0; di--) {
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
Arrays.fill(mem[di][x1][y1][x2], -1);
for (int y2 = 0; y2 < h; y2++) {
mem[di][x1][y1][x2][y2] = count(x1, y1, x2, y2, di, grid, d, mem);
}
}
}
}
}
return mem[0];
}
private int[][][][] multiply(int[][][][] a, int[][][][] b) {
int w = a.length;
int h = a[0].length;
int[][][][] m = new int[w][h][w][h];
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
for (int y2 = 0; y2 < h; y2++) {
for (int x = 0; x < w; x++) {
for (int y = 0; y < h; y++) {
m[x1][y1][x2][y2] += (int) (((long) a[x1][y1][x][y] * b[x][y][x2][y2]) % DIV);
m[x1][y1][x2][y2] %= DIV;
}
}
}
}
}
}
return m;
}
private int[][][][] power(int[][][][] matrix, int power) {
if (power == 1) {
return matrix;
}
if (power == 2) {
return multiply(matrix, matrix);
}
int[][][][] result = power(power(matrix, power / 2), 2);
if (power % 2 == 1) {
result = multiply(result, matrix);
}
return result;
}
public int solution(int[][] grid, int[] d, int k) {
int[][][][] matrix = buildCountMatrix(grid, d);
matrix = power(matrix, k);
int count = 0;
int w = matrix.length;
int h = matrix[0].length;
//noinspection ForLoopReplaceableByForEach Suppress for better readability.
for (int x1 = 0; x1 < w; x1++) {
for (int y1 = 0; y1 < h; y1++) {
for (int x2 = 0; x2 < w; x2++) {
for (int y2 = 0; y2 < h; y2++) {
count += matrix[x1][y1][x2][y2] % DIV;
count %= DIV;
}
}
}
}
return count;
}
}
02024. 06. 17.

Java
Getter / Setter 제대로 사용하기
자바에서 접근 제어자를 처음 배울 때 Getter와 Setter에 대해서도 같이 배우게 된다.
하지만 getter와 setter를 잘못 설명하고 있는 경우가 많은 것 같아 이들을 어떤 경우에 사용해야 하는지에 대해 적어보고자 한다.
잘못된 예제
많은 예제들이 캡슐화라고 하면서 멤버 필드를 private으로 만들고, getter, setter 메서드를 통해 해당 필드에 접근하게 한다.
public class Meaningless {
private int value = 0;
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
}
위의 코드는 멤버 필드를 public으로 두는 것과 다를 바 없다. 외부에서는 해당 값을 그대로 읽고, 값을 덮어쓸 수 있다.
public class Same {
public int value = 0;
}
오히려 메서드 호출 오버헤드가 발생하고 불필요한 코드가 생기는 셈이니 더 나쁘다고도 할 수 있다.
Getter와 setter는 메서드로서의 역할을 다 할 때 그 의미가 생긴다.
외부에서 값을 덮어쓰는 것을 막을 때
게임에서 점수 시스템을 만든다고 해보자.
코인을 획득하면 1점, 적을 처치하면 5점이 오른다.
이를 관리하는 Score 클래스는 다음과 같이 작성할 수 있다.
public class Score {
private int score = 0;
public int getScore() {
return score;
}
public void coinEarned() {
score += 1;
}
public void enemyKilled() {
score += 5;
}
}
score는 클래스 내부에 숨겨두고, score를 증가시킬 수 있는 메서드만 외부에 공개함으로써 score를 직접적으로 변경하지 못하게 차단하였다. 이를 통해 score는 이 클래스 내부에서만 관리한다는 제약을 걸어, 외부에서 예상하지 못하게 값을 수정하는 일에 대해 걱정하지 않아도 되게 되었다.
값을 제한할 때
특정 범위 내의 값을 관리한다고 생각해보자. 이 클래스는 다음과 같이 작성할 수 있다.
public class ClampedValue {
public final int min;
public final int max;
private int value = 0;
public ClampedValue(int min, int max) {
this.min = min;
this.max = max;
}
public int getValue() {
return value;
}
public void setValue(int value) {
if (value < min) {
this.value = min;
} else if (value > max) {
this.value = max;
} else {
this.value = value;
}
}
}
한 멤버 필드에 대해서 getter와 setter가 있지만, setter에서 해당 필드의 값을 제한하는 처리를 한다.
객체 필드일 때
필드가 객체인 경우, 그리고 해당 객체가 불변 객체가 아닐 경우 이를 외부에 그대로 노출하는 것은 매우 위험하다.
이를 해결하기 위해서 getter에서 객체를 복사하여 넘겨줄 수 있다.
숫자들의 합을 구하면서 그 과정을 기록하는 RecordedSum 클래스를 살펴보자.
public class RecordedSum {
private final List<Integer> history = new ArrayList<>();
private int sum = 0;
public List<Integer> getHistory() {
return Collections.unmodifiableList(history);
}
public int getSum() {
return sum;
}
public void add(int value) {
history.add(value);
sum += value;
}
}
이 예제에서는 List인 history를 외부에서 요구할 때 불변 리스트로 변환하여 반환한다.
이렇게 함으로써 외부에서 history를 함부로 수정할 수 없게 하여 history는 RecordedSum 클래스 내부에서만 관리할 수 있도록 할 수 있다.
이렇게 getter와 setter가 의미 있게 사용될 수 있는 경우들을 살펴보았다.
public 멤버가 나쁜 것이 아니다.
해당 멤버의 값이 변함으로써 발생하는 사이드 이펙트가 없고, 외부에서 자유롭게 변경하도록 의도된 것이라면 public으로 공개해주는 것이 좋은 설계가 될 수 있다.
public이 될 수 있는 멤버를 굳이 private으로 숨기면서 의미 없는 getter와 setter를 사용하는 일이 없도록 하자.
02024. 06. 14.

프로그래머스 > Java로 코테풀기
아날로그 시계 - Lv 2 문제 풀이 (실수 비교 안하기)
https://school.programmers.co.kr/learn/courses/30/lessons/250135
주어진 시간 범위 내에서 초침이 분침 / 시침과 겹치는 횟수를 세는 문제이다.
문제 이해하기
다음과 같은 조건들로 인해 제약 사항이 생긴다.
각 바늘은 연속적으로 움직인다.바늘이 겹치는 시간이나 각도가 실수이기 때문에 정확한 비교는 힘들다.
1초 안에 초침이 다른 하나의 바늘과 두 번 겹치는 경우는 없다.초침-분침, 초침-분침 과 같이 분침과 두 번 겹칠 일은 없다.
다만, 초침-분침, 초침-시침과 같이 서로 다른 두 바늘과 겹칠 수는 있다.
간단히 생각하면, 그냥 1초씩 시간을 흘려가면서 각 바늘의 각도를 계산해가면서 초침이 분침이나 시침의 각도를 넘어서는 횟수를 세주면 될 것이다. 딱 여기까지라면 정말 Lv2인 이 문제에 알맞는 난이도라고 생각했을 것이다.
하지만 문제는 시침과 분침, 초침이 한 번에 겹치게 되면 한 번으로 세주어야 하는 데에서 발생했다. 위 접근법은 1초 내에 초침이 분침 또는 시침과 겹친 적이 있는지를 판별할 수는 있지만, 셋 모두가 동시에 겹쳤다는 것을 판단할 수는 없다. 분침-시침이 겹치는 것을 별도로 판별했다고 하더라도, 이 시점이 초침과 겹쳐지는 시점과 달라질 수 있기 때문에 정확하지 않다.
세 바늘이 동시에 겹쳤는지를 판단하기 위해서는 1초 내에서도 언제 겹쳤는지 정확한 시간을 계산하여 비교하던가, 바늘이 겹쳤을 때의 정확한 각도를 계산하여 비교할 수 있어야 한다.
나이브한 접근 - 실수 비교
이게 Lv 2라고? 하는 생각이 들어 다른 사람들의 풀이를 찾아보았다. 놀랍게도 대다수의 사람들이 무려 실수 비교를 통해 바늘이 겹치는 것을 검사하고 있었다. 세 바늘의 각도를 double로 표현하고, 이 각도가 서로 일치하는지를 검사한 것이다.
조금 세게 말하자면, 정말 말도 안되는 풀이라고 생각했다.
프로그래밍을 처음 공부할 때 배우는 것이 실수형의 한계이다. 컴퓨터는 0과 1로 한정된 비트 수를 사용하여 실수를 표현하기 때문에 실수를 정확하게 표현할 수 없고, 오차가 발생한다는 것은 누구나 알고 있다.
따라서 실수형을 다룰 때에는 정확한 값을 가지고 있을 것이라는 생각 자체를 하면 안된다. 다시 말해, 실수형에 == 연산은 해당 값에 부동 소수점 오차가 없다는 완벽한 근거 없이는 절대 해서는 안되는 연산이라는 것이다. 이로 인해 실수형은 대부분 비교 연산을 수행하거나, 일정 수준의 threshold를 두고, 해당 오차 범위 안의 값인지를 검사한다.
그런데 정확성이 중요한 코딩 테스트에서 실수형 비교를 통해 문제를 해결한다니, 말이 안된다고 생각했다.
이러한 방법을 사용한 풀이가 통과된 것은, 단순히 시침, 분침, 초침이 겹치는 시간이 12시 00분 00초 밖에 없기 때문이다. 이 때는 각도가 0이므로 소수점 오차가 발생하지 않는다. 만약 다른 각도에서 세 바늘이 겹치는 현상이 발생했다면, 이 코드들은 통과하지 못했을 것이다.
또, 정확히 12시에만 세 바늘이 겹친다는 것을 알고 있었다면 실수형 비교를 할 이유가 없다. 그저 시간이 12시 정각인지를 검사하는 것을 통해 훨씬 간단하게 체크할 수 있기 때문이다. 다시 말해, 각도를 실수로 표현하고, 이를 동등 비교하는 것은 이 문제 풀이에서 나와서는 안되는, 운으로 통과하는 케이스라고 생각한다.
구현으로 풀기
세 바늘의 각도를 비교해야 한다는 것에는 이견이 없다. 다만, 이를 실수형으로 나타내고 푸는 것이 위험하다는 것이다. 다행히도, 빡센 구현을 통해 부동 소수점 오차 걱정 없이 문제를 해결할 수 있다.
Fraction 클래스
이를 해결하기 위해서는 각도를 분수로 나타내면 된다. 앞선 포스트 자바로 분수 나타내기에서 다룬 Fraction 클래스를 이용하면 각도를 온전히 나타낼 수 있다. 몇몇 메서드가 이 문제에 맞춰 수정되었지만, 큰 뼈대는 같으니 설명 없이 코드만 첨부한다.
private static class Fraction implements Comparable<Fraction> {
public final long numerator;
public final long denominator;
public Fraction(int value) {
this(value, 1);
}
public Fraction(long numerator, long denominator) {
long gcd = gcd(Math.abs(numerator), Math.abs(denominator));
this.numerator = numerator / gcd;
this.denominator = denominator / gcd;
}
public Fraction add(int value) {
return new Fraction(numerator + value * denominator, denominator);
}
public Fraction add(Fraction other) {
long numerator = this.numerator * other.denominator + this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction subtract(Fraction other) {
long numerator = this.numerator * other.denominator - this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction multiply(Fraction other) {
long numerator = this.numerator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction divide(Fraction other) {
return multiply(other.inverse());
}
public Fraction inverse() {
if (numerator == 0) {
throw new ArithmeticException("Cannot inverse zero.");
}
return new Fraction(denominator, numerator);
}
public Fraction mod(int value) {
return new Fraction(numerator % (value * denominator), denominator);
}
public double value() {
return (double) numerator / denominator;
}
@Override
public boolean equals(Object object) {
if (this == object) return true;
if (object == null || getClass() != object.getClass()) return false;
Fraction other = (Fraction) object;
return numerator == other.numerator && denominator == other.denominator;
}
@Override
public int compareTo(Fraction f) {
if (equals(f)) {
return 0;
} else if (value() < f.value()) {
return -1;
} else {
return 1;
}
}
private static long gcd(long a, long b) {
if (b == 0) return a;
return gcd(b, a % b);
}
}
Clock 클래스
시계를 나타내는 Clock 클래스이다. 세 바늘의 각도와 현재 시간, 초침이 다른 바늘과 겹치는 연산을 수행해줄 클래스가 될 것이다.
먼저, 각 바늘이 초 당 몇 도나 회전하는지를 Fraction으로 나타내어준다.
시침은 360도를 12(시간)* 60(분) * 60(초) 만에 돈다.
분침은 360도를 60(분) * 60(초) 만에 돈다.
초침은 360도를 60(초) 만에 돈다.
private static class Clock {
private static final Fraction HOUR_APS = new Fraction(360, 12 * 60 * 60);
private static final Fraction MINUTE_APS = new Fraction(360, 60 * 60);
private static final Fraction SECOND_APS = new Fraction(360, 60);
}
다음으로, 현재 시간과 각 바늘의 각도를 Fraction으로 나타내어준다.
private Fraction time;
private Fraction hourAngle;
private Fraction minuteAngle;
private Fraction secondAngle;
생성자에서는 현재 시간을 입력 받고, 이에 맞게 각 바늘의 각도를 계산해준다.
여기서 중요하게 생각해야 할 점이 바로 초침이 시침이나 분침보다 빠르다는 점이다.
이는 초침이 각도 상 뒤에 있어야 (즉, 더 작은 각도를 가지고 있어야) 분침과 시침을 따라잡는 연산이 쉬워진다는 의미이다.
따라서, 분침이나 시침이 초침보다 더 작은 각도를 가지고 있다면, 한 바퀴를 추가로 회전시켜 (360을 더하여) 더 큰 각도를 가지고 있게 만들어준다.
public Clock(int time) {
this.time = new Fraction(time);
alignAngles();
}
private void alignAngles() {
hourAngle = HOUR_APS.multiply(time).mod(360);
minuteAngle = MINUTE_APS.multiply(time).mod(360);
secondAngle = SECOND_APS.multiply(time).mod(360);
if (minuteAngle.compareTo(secondAngle) <= 0) {
minuteAngle = minuteAngle.add(360);
}
if (hourAngle.compareTo(secondAngle) <= 0) {
hourAngle = hourAngle.add(360);
}
}
다음으로 구현할 메서드는 알람이 울리는 다음 시간으로 이동하고, 해당 시간을 반환하는 nextRing() 메서드이다.
public Fraction nextRing() {
...
}
초침이 분침과 시침을 따라 잡는 시간을 계산하기 위해서는, 각 바늘 사이의 각도와 초 당 얼마만큼의 각도를 초침이 따라잡는지를 알아야 한다.
초침이 분침과 시침을 따라잡는 속도는 각 바늘이 가지는 속도의 차이이므로 다음과 같이 나타낼 수 있다.
private static final Fraction HOUR_FOLLOW_APS = SECOND_APS.subtract(HOUR_APS);
private static final Fraction MINUTE_FOLLOW_APS = SECOND_APS.subtract(MINUTE_APS);
이를 이용하면, 초침이 분침과 시침을 따라잡는 시간은 다음과 같이 계산된다.
Fraction timeToNextHour = hourAngle.subtract(secondAngle).divide(HOUR_FOLLOW_APS);
Fraction timeToNextMinute = minuteAngle.subtract(secondAngle).divide(MINUTE_FOLLOW_APS);
이 두 시간 중 더 빠른 시간에 먼저 종이 울릴 것이므로, 다음과 같이 시간을 업데이트 해준다.
switch (timeToNextHour.compareTo(timeToNextMinute)) {
case -1: // 초침-시침 충돌
case 0: // 초침-시침-분침 충돌
time = time.add(timeToNextHour);
break;
case 1: // 초침-분침 충돌
time = time.add(timeToNextMinute);
break;
}
마지막으로 업데이트된 시간으로 바늘의 각도를 재조정하고, 시간을 반환해준다.
alignAngles();
return time;
nextRing() 메서드는 현재 시간에서 알람이 울리는지는 검사하지 않는다. 따라서 가장 처음 Clock 객체를 생성했을 때 알람이 울리는 시간인지를 판별해 줄 doesRing() 메서드도 하나 넣어준다.
public boolean doesRing() {
return secondAngle.equals(hourAngle.mod(360)) || secondAngle.equals(minuteAngle.mod(360));
}
각도를 실수형이 아니라 정수형을 갖는 분수로 표현했기 때문에 equals() 메서드를 사용해서 정확히 비교할 수 있다.
solution() 메서드
Clock 클래스가 준비되었으면 횟수를 세는 것은 쉽다.
입력받은 시간으로 Clock 객체를 초기화하고, 시간 범위 밖으로 나갈 때 까지 nextRing()을 호출하며, 그 횟수를 세주면 된다.
public int solution(int h1, int m1, int s1, int h2, int m2, int s2) {
int from = h1 * 60 * 60 + m1 * 60 + s1;
int to = h2 * 60 * 60 + m2 * 60 + s2;
Clock clock = new Clock(from);
int count = 0;
if (clock.doesRing()) {
count = 1;
}
while (true) {
double time = clock.nextRing().value();
if (time > to) return count;
count += 1;
}
}
마무리
분수와 시계의 구현을 통해 프로그래머스 PCCP 기출문제 아날로그 시계를 풀어 보았다.
구현할 양이 많기는 해서 Lv 2는 아닌 것 같긴 하다.
내 생각이지만, Lv 2라고 매겨놓은 근거는 구현으로 푸는 것이 아니라 실제로 바늘이 언제 겹치는지는 손으로 미리 계산을 하고, 주어진 시간 범위 내에 겹치는 사건이 얼마나 발생하는지를 판별하라는 것 같다.
그런데 이 방법도 마찬가지로 초침과 분침, 초침과 시침이 얼마나 겹치는지는 계산할 수 있을 것 같은데, 초침-분침-시침이 모두 한 번에 겹치는 것이 12시 정각밖에 없다는 것을 어떻게 증명하는지를 사실 잘 모르겠다.
전체 코드
public class Solution {
private static class Fraction implements Comparable<Fraction> {
public final long numerator;
public final long denominator;
public Fraction(int value) {
this(value, 1);
}
public Fraction(long numerator, long denominator) {
long gcd = gcd(Math.abs(numerator), Math.abs(denominator));
this.numerator = numerator / gcd;
this.denominator = denominator / gcd;
}
public Fraction add(int value) {
return new Fraction(numerator + value * denominator, denominator);
}
public Fraction add(Fraction other) {
long numerator = this.numerator * other.denominator + this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction subtract(Fraction other) {
long numerator = this.numerator * other.denominator - this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction multiply(Fraction other) {
long numerator = this.numerator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction divide(Fraction other) {
return multiply(other.inverse());
}
public Fraction inverse() {
if (numerator == 0) {
throw new ArithmeticException("Cannot inverse zero.");
}
return new Fraction(denominator, numerator);
}
public Fraction mod(int value) {
return new Fraction(numerator % (value * denominator), denominator);
}
public double value() {
return (double) numerator / denominator;
}
@Override
public boolean equals(Object object) {
if (this == object) return true;
if (object == null || getClass() != object.getClass()) return false;
Fraction other = (Fraction) object;
return numerator == other.numerator && denominator == other.denominator;
}
@Override
public int compareTo(Fraction f) {
if (equals(f)) {
return 0;
} else if (value() < f.value()) {
return -1;
} else {
return 1;
}
}
private static long gcd(long a, long b) {
if (b == 0) return a;
return gcd(b, a % b);
}
}
private static class Clock {
private static final Fraction HOUR_APS = new Fraction(360, 12 * 60 * 60);
private static final Fraction MINUTE_APS = new Fraction(360, 60 * 60);
private static final Fraction SECOND_APS = new Fraction(360, 60);
private static final Fraction HOUR_FOLLOW_APS = SECOND_APS.subtract(HOUR_APS);
private static final Fraction MINUTE_FOLLOW_APS = SECOND_APS.subtract(MINUTE_APS);
private Fraction time;
private Fraction hourAngle;
private Fraction minuteAngle;
private Fraction secondAngle;
public Clock(int time) {
this.time = new Fraction(time);
alignAngles();
}
public boolean doesRing() {
return secondAngle.equals(hourAngle.mod(360)) || secondAngle.equals(minuteAngle.mod(360));
}
public Fraction nextRing() {
Fraction timeToNextHour = hourAngle.subtract(secondAngle).divide(HOUR_FOLLOW_APS);
Fraction timeToNextMinute = minuteAngle.subtract(secondAngle).divide(MINUTE_FOLLOW_APS);
switch (timeToNextHour.compareTo(timeToNextMinute)) {
case -1: // 초침-시침 충돌
case 0: // 초침-시침-분침 충돌
time = time.add(timeToNextHour);
break;
case 1: // 초침-분침 충돌
time = time.add(timeToNextMinute);
break;
}
alignAngles();
return time;
}
private void alignAngles() {
hourAngle = HOUR_APS.multiply(time).mod(360);
minuteAngle = MINUTE_APS.multiply(time).mod(360);
secondAngle = SECOND_APS.multiply(time).mod(360);
if (minuteAngle.compareTo(secondAngle) <= 0) {
minuteAngle = minuteAngle.add(360);
}
if (hourAngle.compareTo(secondAngle) <= 0) {
hourAngle = hourAngle.add(360);
}
}
}
public int solution(int h1, int m1, int s1, int h2, int m2, int s2) {
int from = h1 * 60 * 60 + m1 * 60 + s1;
int to = h2 * 60 * 60 + m2 * 60 + s2;
Clock clock = new Clock(from);
int count = 0;
if (clock.doesRing()) {
count = 1;
}
while (true) {
double time = clock.nextRing().value();
if (time > to) return count;
count += 1;
}
}
}
02024. 06. 09.

Java
자바로 분수 나타내기
프로그래머스 문제 중 Lv 2짜리 아날로그 시계라는 문제를 봤다.
주어진 시간 범위 내에 초침이 시침, 분침과 겹치는 횟수를 세는 문제인데,
이 횟수를 세는 것은 그렇게 어렵지 않았지만 난관은 시침, 분침, 초침이 모두 겹칠 때에는 한 번으로 세어야 한다는 점이었다.
이 부분에서 분수를 나타낼 필요성을 느껴 분수를 다루는 클래스를 작성해 보았다.
생성자
가장 먼저, 분수에 있어서 필요한 분자와 분모를 정수형으로 선언해 주었다.
값을 나타내는 용도의 클래스인 만큼, final을 붙여 불변성을 부여하였다.
final로 선언된 원시 자료형이기 때문에, 이 두 값은 클래스 내부에서 관리함에도 불구하고 public으로 선언될 수 있다.
외부에서 자유롭게 참조는 가능하지만, final이 붙었기 때문에 값을 변경할 수 없기 때문이다.
public class Fraction {
public final long numerator;
public final long denominator;
}
가장 베이스가 되는 생성자로는 이 두 값을 입력받는 생성자를 정의하였다.
이때, 최대 공약수로 numerator와 denomiator를 나누어 주어 약분까지 해주었다.
public Fraction(long numerator, long denominator) {
long gcd = gcd(Math.abs(numerator), Math.abs(denominator));
this.numerator = numerator / gcd;
this.denominator = denominator / gcd;
}
private static long gcd(long a, long b) {
if (b == 0) return a;
return gcd(b, a % b);
}
그리고 조금 더 편하게 사용할 수 있도록 디폴트 생성자와 정수를 입력받는 생성자를 오버로딩 하였다.
public Fraction() {
this(0);
}
public Fraction(long value) {
this(value, 1);
}
덧셈, 뺄셈, 곱셈
덧셈, 뺄셈, 곱셈은 각 연산의 정의대로 구현하였다.
이 때, 새로운 Fraction 객체를 생성하여 반환함으로써 불변성을 유지하였다.
또, 생성자에서 약분을 하므로, 모든 Fraction 객체는 기약 분수 상태를 항상 확보하게 된다.
public Fraction add(Fraction other) {
long numerator = this.numerator * other.denominator + this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction subtract(Fraction other) {
long numerator = this.numerator * other.denominator - this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction multiply(Fraction other) {
long numerator = this.numerator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
역수, 나눗셈
나눗셈의 경우 그대로 구현할 수 도 있지만, 역수를 구한 후 곱셈으로 처리하는 것이 구현 상 간단하다.
다만, 분수가 0인 경우 역수를 구할 수 없으므로 이런 경우에는 Exception을 발생시켜 준다.
수학 연산 중 발생한 Exception이니 ArithmeticException을 발생시킨다.
public Fraction inverse() {
if (numerator == 0) {
throw new ArithmeticException("Cannot inverse zero.");
}
return new Fraction(denominator, numerator);
}
나눗셈은 이를 이용하여 역수를 구해, 곱해주기만 하면 된다.
public Fraction divide(Fraction other) {
return multiply(other.inverse());
}
근사치
분수가 나타내는 근삿값을 알기 위한 메서드도 추가해 준다.
public double value() {
return (double) numerator / denominator;
}
Object 메서드
값을 나타내는 클래스이니, 동등 비교와 해시 등의 메서드 오버라이딩을 해주어야 한다.
이를 해주지 않으면, Collection 컨테이너들을 사용할 때 해당 컨테이너들이 제 힘을 발휘하지 못하게 됨은 물론, 두 분수를 비교할 때나 그 값을 확인할 때에도 불편해진다.
@Override
public String toString() {
return String.format("%d / %d", numerator, denominator);
}
@Override
public boolean equals(Object object) {
if (this == object) return true;
if (object == null || getClass() != object.getClass()) return false;
Fraction other = (Fraction) object;
return numerator == other.numerator && denominator == other.denominator;
}
@Override
public int hashCode() {
return Objects.hash(numerator, denominator);
}
전체 코드
import java.util.Objects;
public class Fraction implements Comparable<Fraction> {
public final long numerator;
public final long denominator;
public Fraction() {
this(0);
}
public Fraction(int value) {
this(value, 1);
}
public Fraction(long numerator, long denominator) {
long gcd = gcd(Math.abs(numerator), Math.abs(denominator));
this.numerator = numerator / gcd;
this.denominator = denominator / gcd;
}
public Fraction add(int value) {
return new Fraction(numerator + value * denominator, denominator);
}
public Fraction add(Fraction other) {
long numerator = this.numerator * other.denominator + this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction subtract(Fraction other) {
long numerator = this.numerator * other.denominator - this.denominator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction multiply(int multiplier) {
return new Fraction(numerator * multiplier, denominator);
}
public Fraction multiply(Fraction other) {
long numerator = this.numerator * other.numerator;
long denominator = this.denominator * other.denominator;
return new Fraction(numerator, denominator);
}
public Fraction divide(Fraction other) {
return multiply(other.inverse());
}
public Fraction inverse() {
if (numerator == 0) {
throw new ArithmeticException("Cannot inverse zero.");
}
return new Fraction(denominator, numerator);
}
public Fraction mod(int value) {
return new Fraction(numerator % (value * denominator), denominator);
}
public double value() {
return (double) numerator / denominator;
}
@Override
public String toString() {
return String.format("%d / %d", numerator, denominator);
}
@Override
public boolean equals(Object object) {
if (this == object) return true;
if (object == null || getClass() != object.getClass()) return false;
Fraction other = (Fraction) object;
return numerator == other.numerator && denominator == other.denominator;
}
@Override
public int hashCode() {
return Objects.hash(numerator, denominator);
}
@Override
public int compareTo(Fraction f) {
if (equals(f)) {
return 0;
} else if (value() < f.value()) {
return -1;
} else {
return 1;
}
}
private static long gcd(long a, long b) {
if (b == 0) return a;
return gcd(b, a % b);
}
}
02024. 06. 09.

일상
나는 왜 자바로 코딩 테스트 책을 썼는가
누구나 가슴 속에 책 한 권 쯤은 써보고 싶다는 생각이 있을 것이다. 나 또한 막연히 책을 쓰고 싶다는 생각을 하고 있었고, C++이나 자바 기본서와 같이 아무 주제나 잡고 끄적여도 보고, 대충 목차를 세워보기도 했지만 한 페이지는 커녕 몇 줄 끄적이다 말기를 반복하고 있었다.
그러던 어느 날, 대학교 동기들 몇 명이 모여 있는 단톡방에서 길벗 출판사가 코딩 테스트를 주제로 책을 집필할 작가를 구하고 있다는 소식을 듣고 바로 지원했다. 출판사와 계약을 하고, 강제성이 생기면, 뭔가 할 수 있을 것 같았다. 또, 내 모든 걸 활용해서 쓰기에도 아주 적합한 주제라고 생각했다.
나는 나의 강점과 약점을 알고 있다. 나는 사실 알고리즘에 대해 잘 아는 편이 아니다. 국제 대회는 커녕 학교 대회에서도 열심히 문제를 푸는 팀원의 입에 피자를 넣어주는 역할이었다. 딱 코딩 테스트는 통과할 수 있을 만큼의 필수적인 지식만을 가지고 있다. 반대로 무언가를 구현하거나 설계하는 것에 자신이 있다. (물론 구글에 들어오고 나서 역시나 세상은 넓다는 것을 여실히 느끼고 있다)
코딩 테스트만을 위한 필수 지식을 좋은 코드로 풀어내기. 내가 이 책을 쓰면서 항상 되새겼던 목표였다.
계약 전 집필할 수 있는 언어에는 파이썬과 자바 두 옵션이 있었는데 나는 자바를 선택했다. 파이썬이 특유의 쉬운 난이도로 인해 코딩 테스트에서 더욱 인기가 많다는 것은 알고 있었지만 별다른 고민 없이 자바를 고를 수 있었던 이유는 두 가지가 있다.
1. 자바가 더 자신 있어서
단순한 이유이다. 나는 언어는 언어답게 써야 한다고 생각한다. 언어마다 특징이 있고, 코딩 스타일이 있다. 언어를 언어답게 쓰지 않은 코드는 읽기도 힘들고 언어에 대한 전문성이 떨어져보이게 함은 물론, 언어의 능력을 끌어낼 수 없다. 나는 프로그래밍의 시작을 자바로 했기 때문에 파이썬을 파이썬답게 쓰는 것 보다 자바를 자바답게 쓰는 것에 더 익숙하고 자신이 있다.
코딩 테스트 책이라고 해서 문제를 푸는 것만 다루고 싶지 않았다. 코딩 테스트의 문제를 푼다는 것은 문제를 이해하고, 풀이를 떠올리고, 코드로 옮기는 작업이다. 풀이를 떠올리는 것과 코드로 옮기는 것. 두 가지 모두 코딩 테스트의 일부인 것이다.
풀이를 떠올릴 때에는 논리적으로 정확한 풀이를 도출해내는 것에 집중하고, 코드로 옮길 때에는 자바다운 코드로 옮길 수 있도록 하는데에 최대한 집중하여 집필하려고 했다. 이러한 접근으로 생각해보면, 파이썬에 대한 경험이 상대적으로 적은 내가 파이썬으로 코딩 테스트 책을 집필하는 것은 나 스스로한테도 당당하지 못한 일이라고 생각했다.
2. 자바로도 가능하다는 것을 보여주고 싶어서
파이썬이 코딩 테스트 언어로 인기 있는 이유는 다루기 쉬워서이다. 하지만 막상 우리나라는 자바공화국이라고도 불릴 만큼 자바를 많이 활용한다. 나는 이것이 모순이라고 생각했다. 자바를 이용해 프로젝트를 하고, 취업을 준비하는데 막상 코딩 테스트는 파이썬으로 한다는 것은 자바에 대해 익숙하지 않다는 것을 스스로 이야기하는 것이 아닐까 싶었다.
물론 많은 사람들이 자바로 코딩 테스트를 도전해 보았을 것이다. 하지만 문제를 푸는 것도 어려운데 풀이를 찾아보면 파이썬이나 C++ 밖에 없으니 그 중 쉽다고 하는 파이썬으로 빠졌을 확률이 높다.
이렇게 자바를 사용하는 사람들에게 자바로도 충분히 코딩 테스트를 통과할 수 있고, 오히려 자바답게 코딩 테스트를 푸는 과정을 소개함으로써 코딩 테스트 준비가 단순히 취업을 위한 문턱 하나를 넘는 것을 넘어서 자바에 대한 이해도와 자신감을 끌어올리는 과정이 되기를 원했다.
혹시나 자주 사용하던 언어가 있음에도 불구하고 코딩 테스트 대비를 위해 다른 언어를 고려하고 있으면 코딩 테스트에서 지원하는 언어인 한, 자신의 메인 언어를 코딩 테스트에도 활용해보기를 추천한다. 언어에 대한 이해도와 언어를 다룰 수 있는 능력이 성장함을 느낄 수 있을 것이다.
02024. 05. 20.

일상
마인크래프트 - Google Delight
마인크래프트 15주년을 기념해 구글에서 마인크래프트 이스터에그를 만들었다고 한다.
[마인크래프트] 혹은 [minecraft]를 검색하면 페이지 아래에 마인크래프트 아이콘이 표시된다.
이 아이콘을 클릭하면 아이콘은 취소 아이콘으로 변하고 마인크래프트의 캐릭터인 스티브의 팔이 보여진다.
이 상태로 화면에 표시된 검색 결과를 클릭하면 팔이 열심히 움직이며 블럭을 캐듯 검색 결과를 부수기 시작한다.
완전히 부수면 다음과 같이 여러 개의 블럭으로 구성된 마인크래프트의 화면이 나타난다.
여기에 있는 블럭들 또한 클릭하면 부술 수 있다.
또 다른 검색 결과를 부수면 다른 블럭으로 구성된 화면들이 나온다.
아래에 있는 검색 결과를 부수면 마인크래프트의 지하 세계가 나타난다.
물론 실제 마인크래프트처럼 돌아다니거나 블럭을 다시 설치할 수는 없지만, 항상 같은 화면만 보여주는게 아니라 이런 재미난 요소들을 곳곳에 숨겨놓는게 구글 검색의 묘미 중 하나가 아닌가 싶다.
02024. 05. 16.

일상
8키 키보드 만들기 - artsey.io
회사에서 다른 엔지니어 분이 키보드 만들기 g2g를 열어주셔서 참여해보았다.
직접 납땜과 회로 연결을 했는데, 아주 재미있는 세션이었다.
키캡과 키보드 몸체는 3D 프린터로 뽑아주셨고, 나름 청축을 사용한 기계식 키보드이다.
8키 키보드는 장난감같이 생겼지만, 동시 입력을 활용해 사실상 모든 글자를 입력할 수 있다.
동시 입력을 어떻게 처리할지는 MCU에 설치하는 펌웨어에 따라 달렸는데, 이번 세션에서는 artsey.io에서 제공하는 펌웨어를 사용했다.
키보드 동작 원리
키보드의 회로 원리와 동작 방식을 설명해주셨는데, 아주 이해하기 쉽게 잘 알려주셨다.
위 그림과 같이 키보드는 격자 모양으로 배열되어 있는데, 키가 눌렸을 때 눌린 행과 열을 MCU (Micro Controller Unit)에서 감지하여 어떤 키가 입력되었는지를 알 수 있다.
동시 입력은?
그런데 만약 위 그림에서 0과 F를 동시에 눌렀다고 가정하면, 0에 해당하는 X1, Y1과 F에 해당하는 X4, Y4에 신호가 잡히게 될 것이다. 이것을 (X1, Y4)와 (X4, Y1), 즉, 3과 C가 눌린 상황과 어떻게 구분할 수 있을까?
키 입력 감지가 병렬로 진행되는 것이 아니라, X쪽에서 신호를 내보내면, 눌린 키에 해당하는 Y쪽에 신호가 들어오게 되어 이러한 문제는 발생하지 않는다고 하셨다.
다시 말해, 0과 F가 눌린 상황은,
X1에서 신호 보냄 -> Y1에서 신호 잡힘 -> "0"
X2에서 신호 보냄 -> 아무것도 안 잡힘
X3에서 신호 보냄 -> 아무것도 안 잡힘
X4에서 신호 보냄 -> Y4에서 신호 잡힘 -> "F"
이와 같은 처리의 반복으로 동시 입력을 처리할 수 있다는 것이다.
고스팅 현상
각 키를 눌렀을 때 회로에서 어떤 일이 일어나는지를 살펴보자.
키보드의 키는 위 그림과 같이 스위치이다. 키가 눌렸을 때 해당 스위치가 닫혀 Col에서 보낸 신호를 Row에 전달할 수 있게 되는 것이다.
그런데 이렇게 하면 고스팅 현상이라 불리는 문제가 발생한다.
(X2, Y2), (X2, Y3), (X3, Y2)의 세 키를 동시에 누른 상황을 생각해보자.
X2에서 신호를 보내는 경우, Y2와 Y3에서 정상적으로 감지할 수 있다.
하지만 다음 그림과 같이, X3에서 신호를 보내는 경우에 문제가 발생한다.
전기 신호가 닫힌 스위치들을 따라서 Y3에서도 신호가 감지되는 것이다.
결과적으로 (X3, Y3)는 키를 누르지 않았음에도 눌린 것 처럼 신호가 들어오게 된다.
고스팅 현상 해결
이러한 고스팅 현상은 전기 신호가 원래 우리가 의도했던 방향대로 흘러가지 않아서 발생한다.
따라서 스위치와 함께 다이오드를 연결해주면 해결 가능하다.
이제 세 키가 동시에 눌리더라도, 저기가 우리가 의도한 방향대로만 흐르게 되어 고스팅 현상이 일어나지 않는다.
02024. 05. 15.

Flutter
위젯 회전시키기
앱을 만들다보면 한 위젯을 계속 회전시켜야 하는 경우가 있다.
이럴 때 사용하기 좋은 Rotation 위젯을 만들어보았다.
Rotation(
speed: 30, // 1초에 30도 회전
child: Image.network('https://picsum.photos/seed/hyuni/100/200'),
),
이 위젯을 만든 과정을 되짚어보자.
1. 위젯 회전시키기
다음과 같이 Transform 위젯을 이용하면 위젯을 쉽게 회전시킬 수 있다.
import 'dart:math';
import 'package:flutter/material.dart';
class Rotation extends StatelessWidget {
const Rotation({super.key});
@override
Widget build(BuildContext context) {
return Transform.rotate(
angle: 45 / 180 * pi, // radian
child: Image.network('https://picsum.photos/seed/hyuni/100/200'),
);
}
}
2. 회전 애니메이션 주기
여기서 각도를 state로 변환하고, Ticker를 활용하면 회전을 자유자재로 조절할 수 있다.
import 'dart:math';
import 'package:flutter/material.dart';
import 'package:flutter/scheduler.dart';
class Rotation extends StatefulWidget {
const Rotation({super.key});
@override
State<Rotation> createState() => _RotationState();
}
class _RotationState extends State<Rotation> {
late final Ticker? _ticker;
// 1초에 30도 회전
final double speed = 30;
double _angle = 0;
@override
void initState() {
_ticker = Ticker((elapsed) {
setState(() {
_angle = speed * elapsed.inMilliseconds / 1000;
});
});
_ticker?.start();
super.initState();
}
@override
void dispose() {
_ticker?.stop();
_ticker?.dispose();
super.dispose();
}
@override
Widget build(BuildContext context) {
return Transform.rotate(
angle: _angle / 180 * pi, // radian
child: Image.network('https://picsum.photos/seed/hyuni/100/200'),
);
}
}
02024. 05. 13.
